foc 相关算法
MTPA
为什么要用 MTPA
当电机采用 id=0 的控制策略,这种控制方法忽略了磁阻转矩的作用,电磁转钜方程如下:
\[ \tau _e = \frac{3}{2}p[k_e \cdot i_q + (L_d - L_q)\cdot i_d \cdot i_q] \]
转矩分为永磁转矩 Tr 和磁阻转矩 Tm,而 id=0 只剩下 Tr。这会导致电流的利用率不高,系统的效率降低。所以 id=0 的控制比较适用于隐极式电机(Ld=Lq),而对于凸极式电机并不最优,所以需要重新考虑控制策略。
推导过程
电动机电压方程:
\[ \begin{aligned} U_d = rI_d - L_qI_q\omega_e \\ U_q = rI_q + k_E\omega_e + L_dI_d\omega_e \end{aligned} \]
那么电动机消耗对有功功率为:
\[ P = \frac{3}{2}(U_dI_d + U_qI_q) \]
将电动机方程代入功率方程得:
\[ P = \frac{3}{2} r (I_d^2 + I_q^2) + [k_EI_q + (L_d - L_q)I_dI_q]\omega_e \]
电动机的有功功率一部分消耗在绕阻电阻上发热,另一部分用于输出机械功率:

电动机的机械功率为:
\[ P_{mech} = \tau_e \omega_{mech} \]
机械转速与电频率之间的关系为:
\[ \omega_e = p \omega_{mech} \]
所以:
\[ \tau_e \omega_{mech} = \frac{3}{2} r (I_d^2 + I_q^2) + [k_EI_q + (L_d - L_q)I_dI_q] p \omega_{mech} \]
得到电磁转钜公式:
\[ \tau _e = \frac{3}{2}p[k_e \cdot i_q + (L_d - L_q)\cdot i_d \cdot i_q] \]
如果绕阻中电流峰值是 I_s
\[ I_s^2 = I_d^2 + I_q^2 \]
当输出电磁转钜一定时:
\[ I_q = \frac{\tau_e}{\frac{3}{2}p[(k_E) + (L_d - L_q)I_d]} \]
联立上两式得:
\[ I_s^2 = I_d^2 + \left ( \frac{\tau_e}{\frac{3}{2}p[(k_E) + (L_d - L_q)I_d]} \right )^2 \]
上式可以看作是一个关于\(I_d\)的函数,上式有最小值,当电磁转钜一定时,有一个最小峰值电流\(I_s\),取\(I_s\)最小时有:
\[ \begin{aligned} \frac{\partial I_s^2}{\partial I_d} &= 2I_d + 2I_q \frac{\tau_e}{\frac{3}{2}p} \frac{-(L_d - L_q)}{[k_E + (L_d - L_q)I_d]^2} \\ & = 2I_d + 2I_q \frac{\tau_e}{\frac{3}{2}p[k_E + (L_d - L_q)I_d]} \frac{-(L_d - L_q)}{[k_E + (L_d - L_q)I_d]} \\ & = 2I_d + 2I_q^2\frac{-(L_d - L_q)}{[k_E + (L_d - L_q)I_d]} = 0 \end{aligned} \]
整理得:
\[ (L_d - L_q)I_d^2 + k_EI_d - (L_d - L_q)I_q^2 = 0 \]
求解\(I_d\)得到:
\[ I_d = - \frac{k_E}{2(L_d - L_q)} \pm \sqrt{\left ( \frac{k_E}{2(L_d - L_q)} \right )^2 + I_q^2} \]
如果\(L_d < L_q\)时当电磁转钜一定时电流峰值\(I_s\)最小:
\[ I_d = - \frac{k_E}{2(L_d - L_q)} - \sqrt{\left ( \frac{k_E}{2(L_d - L_q)} \right )^2 + I_q^2} \]
弱磁控制
简介
弱磁控制的这个思想源还是来自他励直流电动机的调磁控制。当他励直流电动机端电压达到最大电压时,只能通过调节电机的励磁电流,进而改变励磁磁通,在保证输出电压最大值不变的条件下,使电机能恒功率运行于更高的转速。也就是说,他励直流电动机可以通过降低励磁电流达到弱磁扩速的目的。对于 PMSM 而言,励磁磁动势因永磁体产生而无法调节,只能通过调节定子电流,即增加定子直轴去磁电流分量来维持高速运行时电压的平衡。达到弱磁扩速的目的。
推导
很多应用需要马达工作在高于额定速度的范围内,这里就需要弱磁控制来实现,电流的电压约束条件如下:
\[ (L_qI_q)^2 + (k_E + L_dI_d)^2 \leqslant \frac{U_{1-limit}^2}{\omega_e^2} \]
电流幅值约束条件:
\[ I_d^2 + I_q^2 \leqslant I_{s-limit}^2 \]
MTPA 下有\(I_d\):
\[ MTPA: I_d = \left\{\begin{matrix} - \frac{k_E}{2(L_d - L_q)} + sign(L_d - L_q) \sqrt{\left ( \frac{k_E}{2(L_d - L_q)} \right )^2 + I_q^2}, L_d \neq L_q\\ 0, L_d = L_q \end{matrix}\right. \]
其中:
\[ sign(x) = \left\{\begin{matrix} 1, x > 0\\ 0, x = 0\\ -1, x < 0 \end{matrix}\right. \]
弱磁情况下有\(I_d\):
\[ I_d = \left\{\begin{matrix} -\frac{k_E}{L_d}+ \frac{\sqrt{(\frac{U_{1-limit}}{\omega_e})^2 - (L_qI_q)^2}}{L_d}, \frac{U_{1-limit}}{\omega_e} \geq L_qI_q\\ n/a, \frac{U_{1-limit}}{\omega_e} < L_qI_q \end{matrix}\right. \]
电流前馈
前馈理论
前馈控制是按照扰动量进行补偿都开环控制,当系统出现扰动时,按照扰动量当大小直接产生矫正作用。
前馈控制结构图如下: 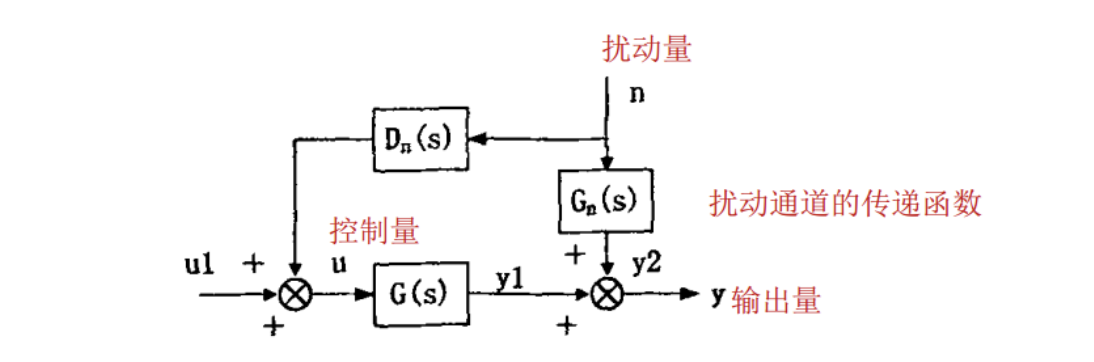
图中\(G_n(s)\)是被控对象扰动通道的传递函数,\(D_n(s)\)是前馈控制器的传递函数,\(G(s)\)为被控对象控制通道传递函数,n、u、y 分别为扰动量、控制量和输出量 假定输入量 u1=0,则有:
\[ Y(s) = Y_1(s) + Y_2(s) = [D_n(s)G(s) + G_n(s)]N(s) \]
若使前馈控制作用完全补偿扰动作用,则应使\(Y(s) = 0\)即:
\[ D_n(s)G(s) + G_n(s) = 0 \]
所以前馈控制器的传递函数为:
\[ D_n(s) = - \frac{G_n(s)}{G(s)} \]
在实际应用中。因为前馈控制为一个开环系统。因此常常采用反馈+前馈的复合控制方式。
电机控制中的前馈控制
在电机控制中加入前馈控制,其结构框图如下: 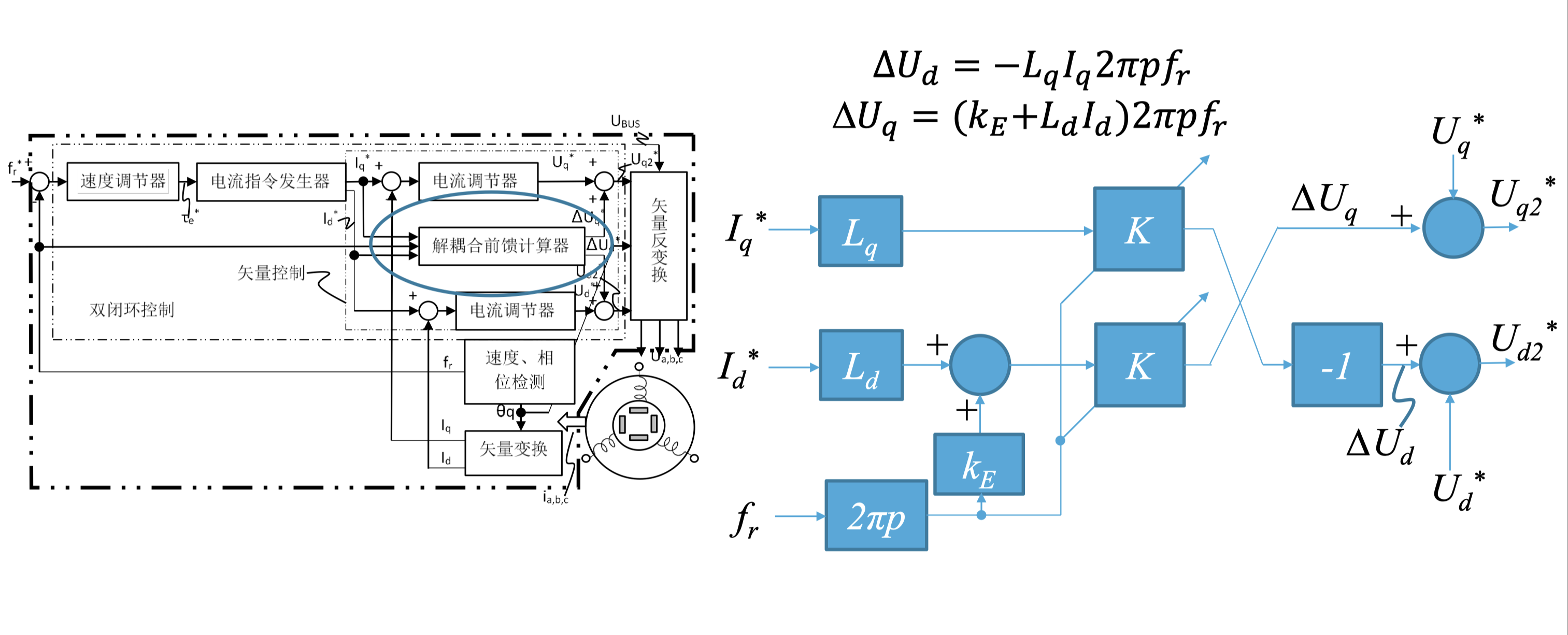
参考文献
《2.ST MC SDK 5.x 矢量控制理论基础》
永磁同步电机也能弱磁调速
永磁同步电机弱磁控制
永磁同步电机-弱磁






