Odriver 之测速
传感器
绝对磁编码器
绝对磁编码器比较简单,直接读寄存器就可以。实际使用中需要配合径向冲磁的磁铁使用,且最好能远离其他可能造成磁场变化的器件;其次需要注意角度更新频率,动态特性等参数。
线性霍尔传感器
对于线性霍尔传感器一般是需要进行校准的,其使用方法一般是两个传感器呈
80 度对称分布,同样需要配合径向冲磁的磁铁使用。 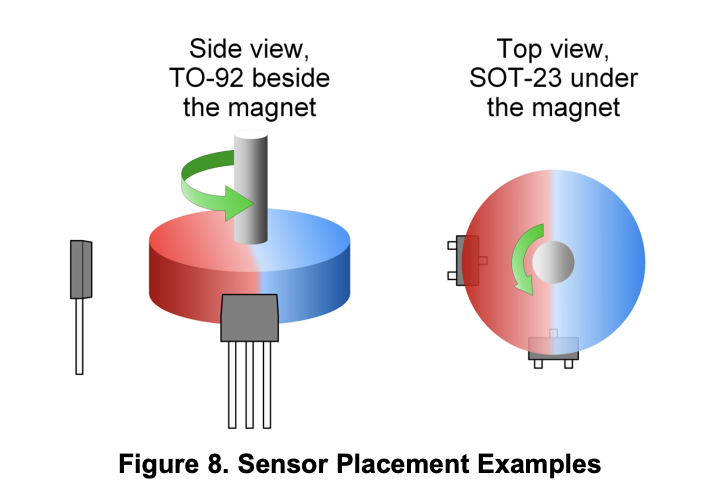
当磁铁旋转一周的时候,线性霍尔的传感器的输出应该正好是一个正弦信号,但是正弦的幅值需要校准,让传感器旋转一周分别获取最大值和最小值,这样就可以重构一周的信号与位置的关系。单个传感器就可以获取全部位置角度的信息,但是单个传感器存在一个问题,就是在正弦波的极点处值的变化非常小,而在线性区域变化则比较明显,因此使用两个传感器呈
90 度摆放则可以解决这个问题。如下图: 
如果 a 传感器取 sin 值为 hall_sin,b 传感器取 cos 值为 hall_cos,则最终的角度为 atan2f(hall_sin, hall_cos)。
1 | /** |
当 sin 在 1 或者-1 附近的时候 cos 值接近 0,因此虽然 sin 值变化很小,但是除以 cos 后就会变化很明显,毕竟 cos 值这个时候是变化最明显的,接近线性状态。同理在 sin 值在 0 附近的时候,cos 在 1 附近,这时 sin 变化明显,sin 值除以一个 1 附近的值仍然是变化明显的。多么美妙的设计啊,神奇的三角函数!
转子角度和速度的状态估计
状态估计
估计器有两种状态:位置和速度。位置以编码器计数为单位,速度以计数/秒为单位。由于编码器在我们转完一整圈时不断计数,我们可以想象状态是沿着展开的线而不是角度,因此我们可以谈论位置(以计数为单位)而不是角度。
因此,鉴于位置和速度这两种状态,我们可以做的最简单的事情就是使用速度来预测随时间变化的位置。这对于在离散计数之间插入编码器位置很重要。也就是说,我们始终以一阶(直线)跟踪预期位置,即使我们处于编码器脉冲之间。这提供了更平滑的控制和更高的有效精度。 预测预期角度的位置也很重要,这样我们就可以预测下一个编码器脉冲何时到来。如果它晚了或早了,这给了我们关于我们高估或低估了速度这一事实的信息。所以:这是该预测的代码,速度的超级简单一阶积分:
1 | // Predict current pos |
好的,现在我们执行检查编码器边缘是早还是晚的部分。这围绕着一个 floor 函数,该函数以全浮点精度获取预测角度(就像编码器计数有很多小数位),并告诉我们应该对应的编码器计数。就像如果预测角度是一个斜坡,编码器计数将是一个阶梯。我们使用 floor 函数来做这个从坡道到楼梯的映射。 如果我们预测的角度有点落后,我们的预测还没有切换到下一个位置,但编码器已经切换到下一个位置,delta_pos 将是 1.0f 是实际位置与预测位置的差值。
1 | // discrete phase detector |
所以,我们知道我们是早还是晚,现在我们就此采取行动。假设我们迟到了,我们需要加快速度估计,也就是下面第二行。在第二行中,我们加速(以一定速率增加速度)与我们的位置误差成正比:就像质量弹簧系统一样。同样,在没有阻尼的情况下,它会形成谐波振荡器并围绕正确值振荡。所以我们需要添加阻尼。这是通过将位置估计值也更接近测量值来完成的,因此是下面的一行。解释它的另一种方法是我们有一个 PI 循环,其中编码器是我们尝试使用一些有限带宽跟踪的输入信号。
1 | // pll feedback |
边界处理
1 | // if we are stopped, make sure we don't randomly drift |
如果速度为 0,则将插值强制设置为 0.5,仅是取一个中间值,实际速度为 0 的可能性很小。当预测误差大于 0 的时候,实际上就是预测值刚好过了传感器测量值的时候,这个时候插值应该很小,当然对于高速转动的时候是不成立的,在低速的时候将插值设置为 0 是可以的。相反当预测误差小于 0 的时候,就是传感器刚好切换到下一个位置的时候,这个时候预测值刚好滞后一个 count(同样只有在低速的时候才成立)这个时候插值应该设置为 1。而当预测误差一个 count 内的时候说明速度比较低,这个时候插值应该根据预测的速度来计算,对预测速度进行积分。但是积分的上下限就是一个 count 即 [0,1]。最后将传感器读出来的值加上插值就是预估的角度。
参数设计
调节
我们如何选择这些增益?与任何过滤器一样,需要权衡延迟与平滑度。合适的值取决于编码器的分辨率和应用程序。高带宽控制需要高带宽状态估计,但代价是对编码器脉冲的反应更敏锐。 更高分辨率的编码器意味着每个脉冲在“阶梯”中具有更小的幅度,因此您得到的反应不那么尖锐,因此您可以针对系统中相同幅度的噪声/振铃调高带宽。
理论
阻尼比
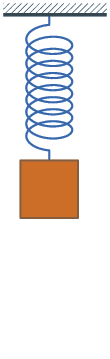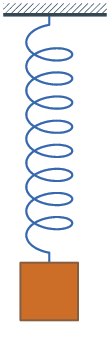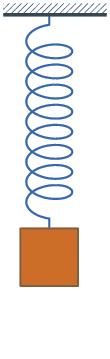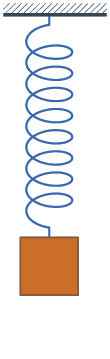
当弹簧质量系统完全没有损耗,质量会一直摆动,不会结束,每一次的摆动振幅都和之前一样,这种理想情形称为无阻尼。 若系统的损耗很大,例如弹簧质量系统放置在黏滞的液体中,系统会慢慢的回到初始位置,甚至不会过冲,这称为过阻尼。 一般而言,在摆动时会出现过冲,再往另一边摆动,再回来,在摆动过程中,系统消耗了一些能量,而摆动振幅也会越来越小,最后回到初始位置,这称为欠阻尼。 在过阻尼及欠阻尼二个条件之间,有一个特定的情形是系统不会过冲,会在最快时间回到初始位置,这称为临界阻尼。临界阻尼和过阻尼都不会过冲,而临界阻尼是最快回到初始位置的那一个阻尼条件。
阻尼比定义
阻尼比常用ζ表示,是二阶微分方程步阶响应及频率响应的参数之一。在控制理论及谐振子中相当重要。阻尼比表示系统的阻尼相对于临界阻尼的比值。
二阶系统相对于阻尼比 ζ 的阶跃响应
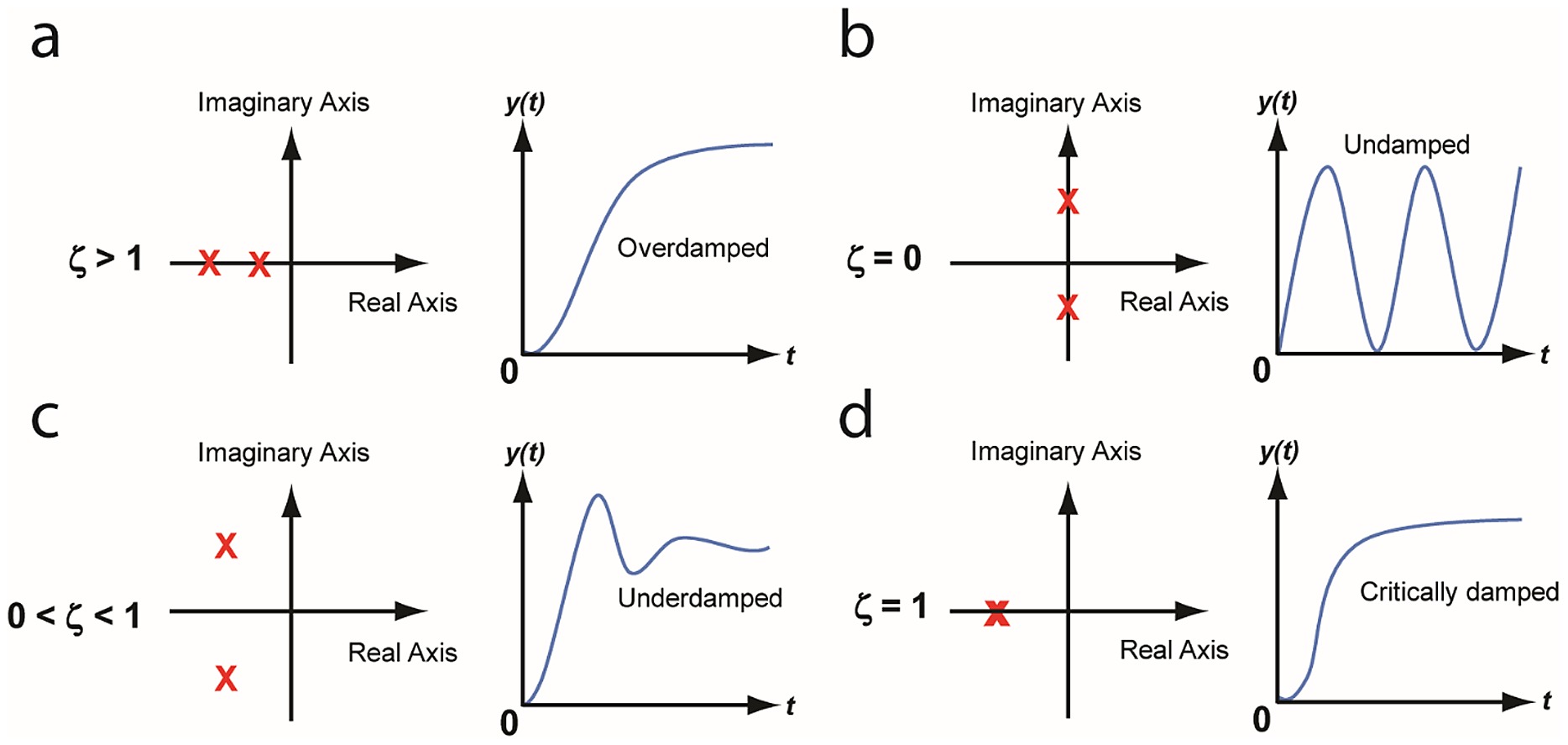
- 过阻尼振荡。阻尼比大于 1,极点均为负实数。系统在没有振荡的情况下达到稳定状态。随着阻尼比的增加,它达到稳态的速度变慢。
- 无阻尼振荡。注意所有的极点都在虚轴上。阻尼比为零,存在无阻尼振荡。
- 欠阻尼振荡。阻尼比在 0~1 之间,极点为负实部的复数。当系统达到稳定状态时,振荡逐渐减小到零。
- 临界阻尼振荡。在没有振荡的情况下以最快的方式达到稳定状态。这两个极点具有相同的负值。
更定量地说,越靠左的极点“越快”(更高的带宽)逼近,具有更大虚部的极点以更高的频率振荡。有什么不同?同样,这最好用图片显示:
请注意,在所有这些中,极点位置的单位可以采用弧度/秒。因此,如果极对位于(-2 ± 5i),那么我们将得到一个频率为 5 弧度/秒的正弦响应,它以 2 弧度/秒的速度衰减。
所以假设蓝色轨迹是响应输入位置突然增加的位置,即编码器输入变化。假设我们希望过滤后的输出尽可能快地跟踪它,而不会过冲。当两个极点(红色的 X)恰好在彼此的顶部时会发生这种情况:这称为临界阻尼(请参见第一张图片中右下角的示例)。
极点
。
推导
假设我们有一些 P 和 I 增益(
所以下面的方程式有两个状态,p 是位置,v
速度。为了清楚起见,我使用了一个变量来 e
表示位置状态和编码器读数之间的误差,后者指定
写成矩阵:
这个系统的极点等于左边矩阵的特征值,系统矩阵,通常称为 A。
好的,矩阵的特征值是多少?有了现代技术,我们可以让计算机为我们做这些:我们使用 SymPy。在 SymPy 现场亲自尝试输入此命令:
1 | Matrix([[-x, 1], [-y, 0]]).eigenvals() |
假装那 x 意味着
我们希望极点的实部是某个特定数字,这是我们的带宽(以弧度/秒为单位),我们希望虚部在两个极点上都为零。
这正是代码中的内容:
1 | motor->rotor.pll_kp = 2.0f * rotor_pll_bandwidth; |
参考文献
https://discourse.odriverobotics.com/t/rotor-encoder-pll-and-velocity/224/4
https://www.ti.com.cn/zh-cn/sensors/magnetic-sensors/linear-hall-effect-sensors/products.html
https://www.ti.com.cn/product/cn/DRV5055
https://figshare.com/articles/figure/Step_response_of_a_second_order_system_with_respect_to_the_damping_ratio_950_the_poles_are_shown_as_X/500243
https://www.wikiwand.com/zh/%E9%98%BB%E5%B0%BC%E6%AF%94
预览: