投影

这里以小孔成像模型为例，全相模型是相同的流程只是投影模型不一样而已。在相机校准模型一文中已经介绍了将像素坐标系变换到相机坐标系中 相机校准模型 如下：

\[ \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{d_x}& 0 &u_o \\ 0 & \frac{1}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\  y \\ 1 \end{bmatrix} = \frac{1}{z_c}\begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_c\\  y_c\\  z_c \end{bmatrix} \]

这里我们取 \(z_c = 1\) 再做一个变换得到：

\[ \begin{bmatrix} x_c\\  y_c\\  z_c \end{bmatrix} =\begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} ^{-1} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} \]

我们记 ：

\[ K_{内参}^{-1} = \begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} ^{-1} \]

则将像素坐标系与该矩阵相乘就可以将像素坐标系转换到相机坐标系上，待后面使用。

IMU 数据处理

具体可以参考 imu 姿态解算 一文，我们需要对 IMU 数据做三件事情：

  • IMU 坐标系对齐相机坐标系，这一步目的为了将 IMU 的正交三轴数据与 Camera 坐标系对齐。

  • 卡尔曼滤波：为了消除 IMU 的系统误差以及如果要做重力矫正需要做姿态解算（重力对齐）。这里常用的就是卡尔曼滤波和 mahony 滤波，这一层滤波的目的就是为了得到更为准确的相机姿态和相机抖动状态，如下图所示：

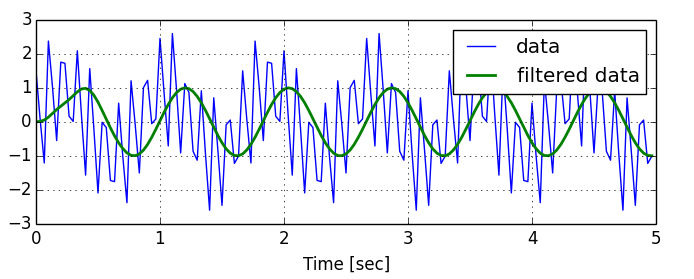
  • 平滑滤波：在我们得到相机的抖动状态就可以对相机的姿态做一个平滑滤波（可以采用四元数求平均，或者高斯滤波等算法），这个平滑滤波的目的是为了得到相机防抖后想要得到的状态。

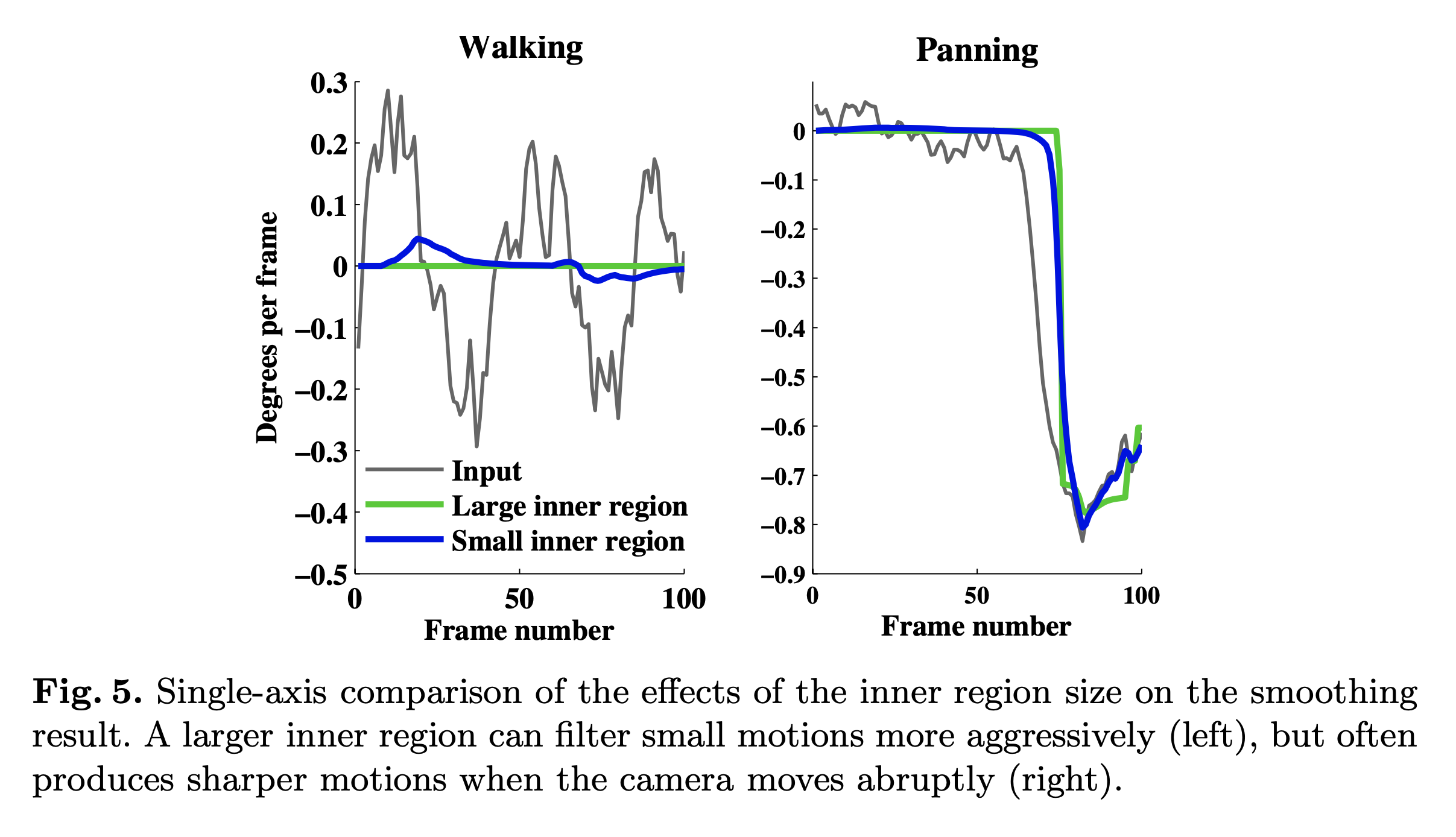
我们将从 Large inner region 曲线或者 Small inner region 曲线到 Input 曲线的变换矩阵记为 \(M(\alpha, \beta, \gamma)\) 为了简化模型这里面的数据是已经将 IMU 坐标系变化到相机坐标系下的变换矩阵。

到这里我们就得到了两条曲线和一个变换矩阵。

求透视变换矩阵

这里我们记旋转矩阵为：

\[ \begin{aligned} M(\alpha, \beta, \gamma) & =\left[\begin{array}{ccc} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{array}\right] \\ & =\left[\begin{array}{ccc} \cos \gamma \cos \beta & -\sin \gamma & \cos \gamma \sin \beta \\ \sin \gamma \cos \beta & \cos \gamma & \sin \gamma \sin \beta \\ -\sin \beta & 0 & \cos \beta \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{array}\right] \\ & =\left[\begin{array}{ccc} \cos \gamma \cos \beta & -\sin \gamma \cos \alpha+\cos \gamma \sin \beta \sin \alpha & \sin \gamma \sin \alpha+\cos \gamma \sin \beta \cos \alpha \\ \sin \gamma \cos \beta & \cos \gamma \cos \alpha+\sin \gamma \sin \beta \sin \alpha & -\cos \gamma \sin \alpha+\sin \gamma \sin \beta \cos \alpha \\ -\sin \beta & \cos \beta \sin \alpha & \cos \beta \cos \alpha \end{array}\right] \end{aligned} \]

综合前面两节的内容我们可以通过如下公式得到投影变换矩阵 R：

\[ R = K_{内参}^{-1} \ast M(\alpha ,\beta ,\gamma ) \ast K_{内参} \]

改写成完整的公式如下：

\[ R = \begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix}^{-1} \ast \left[\begin{array}{ccc} \cos \gamma \cos \beta & -\sin \gamma \cos \alpha+\cos \gamma \sin \beta \sin \alpha & \sin \gamma \sin \alpha+\cos \gamma \sin \beta \cos \alpha \\ \sin \gamma \cos \beta & \cos \gamma \cos \alpha+\sin \gamma \sin \beta \sin \alpha & -\cos \gamma \sin \alpha+\sin \gamma \sin \beta \cos \alpha \\ -\sin \beta & \cos \beta \sin \alpha & \cos \beta \cos \alpha \end{array}\right] \ast \begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} \]

该公式是通过相机的内参矩阵将像素坐标系变换到相机坐标系，然后通过 IMU 得到相机的姿态，将相机坐标系变换到世界坐标系下对相机的姿态进行稳定，得到稳定后的相机姿态，再将上述矩阵的逆乘起来变换回像素坐标系。这样就得到了透视变换的矩阵，将像素的坐标与该 R 矩阵相乘就得到了该像素防抖后的坐标值（就是 opencv 里的 remap）。

特别注意

  • 在做 IMU 姿态解算的时候要给陀螺仪足够的置信度，不然可能很难得到较好的防抖效果。
  • 要将视频帧的时间戳与 IMU 的时间戳对齐，不然一定不能得到较好的效果，笔者没有研究好这块算法手动试出来的，精度要在 1ms 内才行，另外有香港科技大学的 VIO 项目里面有相关论文和实现可以参考。
  • rollingshutter 需要矫正，其实算法上需要做的就是找到帧曝光开始和结束的时刻，然后将旋转矩阵按行进行插值得到每一行的矩阵然后分别对每一行进行应用 remap 就可以了。
  • 这里没有考虑破图问题，实际工程中要考虑破图问题。
  • 这里存在一个问题就是将原图乘透视变换矩阵得到的坐标值大概率是浮点值，但是像素坐标系下只有蒸熟点那么就会造成画质损失，如果想改善这个，可以通过将目标图像乘矩阵 R 的逆得到原图的坐标点，当然这里也会得到浮点坐标坐标值，但是对于原图我们可以通过双线性插值得到变换后的图像值（注意这里是操作图像值而不是坐标值了）。
  • 实际使用中一般不会直接使用旋转矩阵，会改用四元数来处理，便于插值。