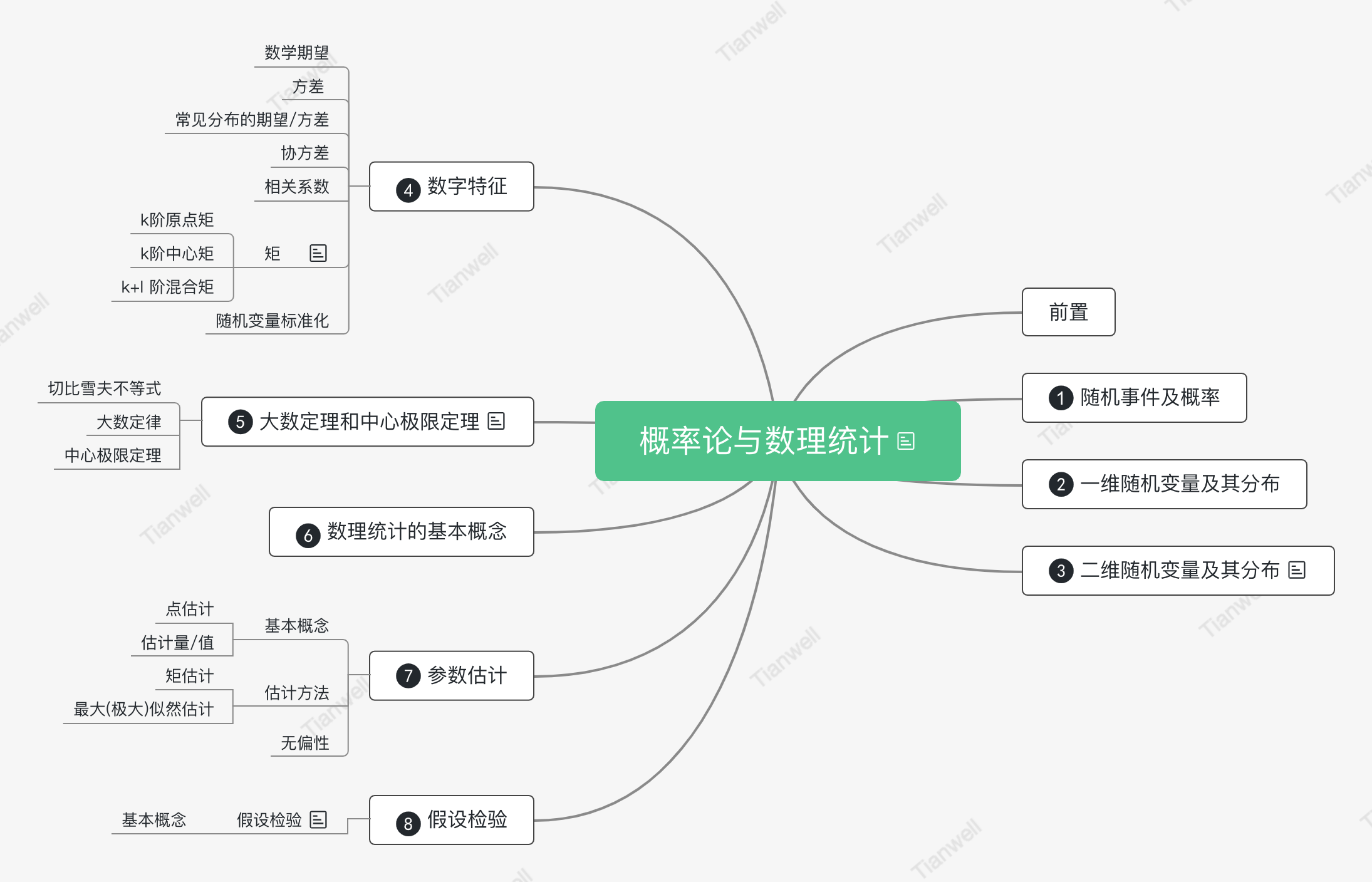
概率论与数理统计

分类于 Science Thought ， Math 阅读次数： 30 Waline：本文字数： 8.9k 阅读时长 ≈ 32 分钟

概率论基本概念

概率的派别

对于概率的定义有几个主流的派别：

频率派：频率派认为如果频率存在稳定性，即当 $n \to \infty$ 时下面极限存在（下面这个写法只是示意，后面介绍大数定律的时候会给出严格的定义），就得到了概率（用 Probability 的首字母 P 来表示）： $P （正面） = lim_{n \to \infty} P_{n} （正面）$
古典派：如果因为无知，使得我们没有办法判断哪一个结果会比另外一个结果更容易出现，那么应该给予它们相同的概率，此称为不充分理由原则（Insufficient Reason Principle）。以不充分理由原则为基础，经由拉普拉斯：之手，确立了古典概率的定义，即：未知的概率都为等概率
主观派：最后介绍下主观派，主观派认为概率是信念强度（degree of belief）。比如说，我个人相信 20 年后人类从网络时代进入人工智能时代的概率为 70%.

三个流派大概有以下的区别： $\begin{array}{cc} 频率派 & 古典派 & 主观派 \\ 理论基础 & 过往事实的归纳总结、 q u a d & 不充分理由原则、 q u a d & 知识和直觉、 q u a d \\ 概率定义 & 频率稳定性、 q u a d & 等概率、 q u a d & 信念强度、 q u a d \end{array}$

概率公理化

已知某样本空间 $Ω$ ，对于其中任一事件 $A$ ，定义函数 $P$ ，满足以下三大公理：

非负性公理： $P (A) \geq 0$
规范性公理： $P (Ω) = 1$
可加性公理：设 $A_{1} 、 A_{2} 、 \dots$ 为两两不相容的事件，即 $A_{i} \cap A_{j} = \emptyset （ i \neq j ）$ ，有： $P (A_{1} \cup A_{2} \cup \dots) = P (A_{1}) + P (A_{2}) + \dots$

则 $P$ 称为概率函数， $P (A)$ 称为事件 A 的概率。

事件之间的运算和关系

并运算：对于事件 $A 、 B$ ，并运算定义为（ $\equiv$ 表示定义）： $A \cup B \equiv {x | x \in A 或 x \in B}$
交运算：对于事件 $A 、 B$ ，交运算定义为： $A \cap B \equiv {x | x \in A 且 x \in B}$
差运算：对于事件 $A 、 B$ ，定义差运算为： $A - B \equiv {x | x \in A 且、 q u a d x \notin B}$
补运算：对于事件 A、B，如果： $A = Ω - B$ 则称 B 为 A 的补，记作（其中 c 代表 Complement）： $B = \overset{―}{A} 或、 q u a d B = A^{c}$
基本运算的性质： $\begin{array}{ccc} 类比、 q u a d & 改写 \\ 并 & + & A \cup B = A + B \\ 交 & \times & A \cap B = A B \\ 差 & - & A - B \end{array}$
德摩根定律： $\overset{―}{A \cup B} = \overset{―}{A} \cap \overset{―}{B}$ = $$
小结： $\begin{array}{ccc} 定义、 q u a d & 类比、 q u a d \\ 并 & A \cup B = {x | x \in A 或 x \in B} & + \\ 交 & A \cap B = {x | x \in A 且 x \in B} & \times \\ 差 & A - B = {x | x \in A 且、 x \notin B} & - \\ 补 & \overset{―}{A} = B ⟺ B = Ω - A \end{array}$
事件之间的关系：

$事件之间的关系 = {\begin{cases} 包含、相等、不相容、对立 \end{cases}$

条件概率

设 A 和 B 是样本空间 $Ω$ 中的两事件，若 $P (B) > 0$ ，则称：

$P (A | B) = \frac{P (A \cap B)}{P (B)}$

为“假设条件为 B 时的 A 的概率”，简称条件概率。也常写作：

$P (A | B) = \frac{P (A B)}{P (B)}$

乘法公式

若 $P (B) > 0$ ，则： $P (A B) = P (B) P (A | B)$
若 $P (A) > 0$ ，则： $P (A B) = P (A) P (B | A)$
若 $P (A_{1} \dots A_{n}) > 0$ ，则： $P (A_{1} \dots A_{n}) = P (A_{1}) P (A_{2} | A_{1}) P (A_{3} | A_{1} A_{2}) \dots P (A_{n} | A_{1} \dots A_{n - 1})$

63 4、贝叶斯与全概率对于同一样本空间 $Ω$ 中的随机事件 $A 、 B$ ，若 $P (B) \neq 0$ ，有： $P (A | B) = \frac{P (A)}{P (B)} P (B | A)$

设 $A_{1} 、 A_{2} 、 \dots 、 A_{n}$ 满足： $A_{i} \cap A_{j} = \emptyset, (i \neq j) 且、 q u a d P (⋃_{i = 1}^{n} A_{i}) = 1$

若 $P (A_{i}) > 0, i = 1, 2, \dots, n$ ，则对任意事件 $B$ 有： $P (B) = \sum_{i = 1}^{n} P (A_{i}) P (B | A_{i})$

有了全概率公式后，可以得到贝叶斯定理真正的样子：设 $A_{1} 、 A_{2} 、 \dots 、 A_{n}$ 为样本空间 $Ω$ 的一个分割，则有： $\begin{aligned} P (A_{i} | B) & = \frac{P (B A_{i})}{P (B)} \\ = \frac{P (B | A_{i})}{P (B)} P (A_{i}) \\ = \frac{P (B | A_{i})}{\sum_{i = 1}^{n} P (A_{i}) P (B | A_{i})} P (A_{i}) \end{aligned}$

也就是把 $P (B)$ 分解到分割 $A_{1} 、 A_{2} 、 \dots 、 A_{n}$ 上去了。

独立事件

对于两个随机事件 $A 、 B$ ，如果满足： $P (A B) = P (A) P (B)$

则称 A 与 B 相互独立，或简称 A 与 B 独立，否则称 A 与 B 不独立或相依。

设 $A_{1} 、 A_{2} 、 \dots$ 为有限个或者无限个事件，从中任取两个 $A_{i 1} 、 A_{i 2}$ ，若满足： $P (A_{i 1} A_{i 2}) = P (A_{i 1}) P (A_{i 2})$

则称 $A_{1} 、 A_{2} 、 \dots$ 是两两独立。

若从中任取有限个 $A_{j 1} 、 A_{j 2} 、 \dots 、 A_{j m}$ ，若满足： $P (A_{j 1} A_{j 2} \dots A_{j m}) = P (A_{j 1}) P (A_{j 2}) \dots P (A_{j m})$

则称 $A_{1} 、 A_{2} 、 \dots$ 是相互独立。

随机变量及其分布

随机变量

定义在样本空间 $Ω$ 上的实值函数： $X = X (ω), ω \in Ω$

称为随机变量。随机变量是一个函数，所以都用大写字母来表示，以示和自变量 x 的区别。

二项分布

概率质量函数

如果 $p (x)$ 满足 $（ x \in {x_{i}}, i = 1, 2, \dots ）$ ：

非负性： $p (x_{i}) \geq 0$
规范性： $\sum_{i = 1}^{\infty} p (x_{i}) = 1$

则称其为概率质量函数（PMF）。

伯努利分布

某样本空间只包含两个元素， $Ω = {ω_{1}, ω_{2}}$ ，在其上定义随机变量 $X$ ： $X = X (ω) = {\begin{cases} 1, & ω = ω_{1} \\ 0, & ω = ω_{2} \end{cases}$

若 $0 \leq p \leq 1$ 时，有：

$p (1) = P (X = 1) = p$

$p (0) = P (X = 0) = 1 - p$

或写作：

$P (X = x) = p (x) = {\begin{cases} p, & x = 1 \\ 1 - p, & x = 0 \end{cases}$

则此概率分布称作 0-1 分布，也称作伯努利分布。

在数学中，类似于扔一次硬币这样的“是非题”称为一次伯努利试验，像上面这样独立地重复扔 n 次硬币（做同样的“是非题”n 次），就称为 n 重伯努利试验。

二项分布

对于 n 重伯努利实验，如果每次得到“是”的概率为 p，设随机变量： $X = 得到 “ 是 ” 的次数$

则称： $p (k) = P (X = k) = (\binom{n}{k}) p^{k} (1 - p)^{n - k}, k = 0, 1, \dots, n$

为随机变量 X 的二项分布，也可以记作： $X \sim b (n, p)$

当 n=1 的时候，对应的就是伯努利分布，所以伯努利分布也可以记作 $b (1, p)$ 。

离散的累积分布函数

设 $X$ 是一个随机变量， $x$ 是任意实数，函数： $F (x) = P (X \leq x) = \sum_{a \leq x} p (a)$

因为是把概率质量函数累加起来，所以称为累积分布函数（Cumulative Distribution Function，或者缩写为 CDF），也简称为分布函数。

离散的数学期望设离散随机变量 $X$ 的概率质量函数为： $p (x_{i}) = P (X = x_{i}), i = 1, 2, \dots, n, \dots$

如果： $\sum_{i = 1}^{\infty} | x_{i} | p (x_{i}) < \infty$ 则称： $E (X) = \sum_{i = 1}^{\infty} x_{i} p (x_{i})$

为随机变量 X 的数学期望（expected value，或，expectation），简称期望或均值（mean），也有很多文档会用 $μ_{X}$ 来表示（如果不强调随机变量的话，也可以直接用 $μ$ 来表示）： $μ_{X} = μ = \sum_{i = 1}^{\infty} x_{i} p (x_{i})$

若级数 $\sum_{i = 1}^{\infty} | x_{i} | p (x_{i})$ 不收敛，则称 $X$ 的数学期望不存在。

学期望也称作矩。更准确点说，由于数学期望： $E (X) = \sum_{i = 1}^{\infty} x_{i} p (x_{i})$ 中 $x_{i}$ 是一次项，所以又称作一阶矩。这个称呼经常在统计的书上会遇到，特在此说明。

数学期望的性质

复合：假设 $g (X)$ 为随机变量 $X$ 的某一函数，则： $E [g (X)] = \sum_{i} g (x_{i}) p (x_{i})$
常数：若 c 为常数，则： $E (c) = c$
线性组合：数学期望满足：
- 齐次性，对于任意常数 $a$ 有： $E (a X) = a E (X)$
- 可加性，对于随机变量的函数 $g_{1} (X) 、 g_{2} (X)$ 有： $E [g_{1} (X) + g_{2} (X)] = E [g_{1} (X)] + E [g_{2} (X)]$
伯努利分布和二项分布的期望分别如下： $\begin{array}{cc} 伯努利分布、 q q u a d & 二项分布、 q q u a d \\ P M F & p (x) = {\begin{cases} p, & x = 1 \\ 1 - p, & x = 0 \end{cases} & p (x) = (\binom{n}{x}) p^{x} (1 - p)^{n - x} \\ μ & p & n p \end{array}$

方差与标准差

方差

代数式： $V a r (X) = E [(X - E (X))^{2}]$ 称为随机变量 X 的方差（Variance），也可记作 $σ^{2}$ 或者 $σ_{X}^{2}$ 。

方差的性质

化简：可以通过下式来化简运算： $V a r (X) = E (X^{2}) - μ^{2}$
常数：若 c 为常数，则： $V a r (c) = 0$
相加与数乘：若 a、b 为常数，则： $V a r (a X + b) = a^{2} V a r (X)$

标准差

假如随机变量 $X$ 的方差为 $V a r (X)$ ，则称：

$σ (X) = \sqrt{V a r (X)}$ 为标准差，也可以记作 $σ$ 或者 $σ_{X}$ 。

二项分布的方差

$\begin{array}{cc} 伯努利分布、 q q u a d & 二项分布、 q q u a d \\ P M F & p (x) = {\begin{cases} p, & x = 1 \\ 1 - p, & x = 0 \end{cases} & p (x) = (\binom{n}{x}) p^{x} (1 - p)^{n - x} \\ μ & p & n p \\ V a r (X) & p (1 - p) & n p (1 - p) \end{array}$

马尔可夫不等式

设 $X$ 为取非负值的随机变量，则对于任何 $a > 0$ ，有： $P (X \geq a) \leq \frac{E (X)}{a}$

切比雪夫不等式

设 $X$ 是一随机变量，均值 $μ$ 和方差 $σ^{2}$ 有限，则对任何 $k > 0$ 有： $P (| X - μ | \geq k) \leq \frac{σ^{2}}{k^{2}}$

泊松分布

对于随机变量 $X$ 的概率质量函数： $P (X = k) = \frac{λ^{k}}{k!} e^{- λ}, k = 0, 1, 2, \dots$ 称为随机变量 $X$ 的泊松分布，也可以记为： $X \sim P (λ)$

其数学期望和方差为：

$E (X) = λ, V a r (X) = λ$

条件
更一般地，在某一段时间 T 内发生特定事件的次数，如果满足以下假设，都可以看作泊松分布：

平稳性：在此时间段 T 内，此事件发生的概率相同（在实际应用中大致相同就可以了）。
独立性：事件的发生彼此之间独立（或者说，关联性很弱）。
普通性：把 T 切分成足够小的区间、Delta T，在、Delta T 内恰好发生两个、或多个事件的可能性为 0（或者说，几乎为 0）。

泊松分布是二项分布的极限： $lim_{n \to \infty} (\binom{n}{k}) {(\frac{μ}{n})}^{k} {(1 - \frac{μ}{n})}^{n - k} = \frac{μ^{k}}{k!} e^{- μ}$

所以在泊松分布的 $λ$ 固定的情况，二项分布的 n 越大（对应的 $p = \frac{λ}{n}$ 越小），此时两者会非常接近。

重要的离散分部

几何分布

对于 n 重伯努利实验，如果每次得到“是”的概率为 p，设随机变量： $X = 首次得到 “ 是 ” 时进行的试验次数$

则称： $p (k) = P (X = k) = (1 - p)^{k - 1} p, k = 1, 2, \dots$

为随机变量 X 的几何分布，也可以记作： $X \sim G e (p)$

其数学期望和方差为： $E (X) = \frac{1}{p}, V a r (X) = \frac{1 - p}{p^{2}}$

负二项分布

对于 n 重伯努利实验，如果每次得到“是”的概率为 p，设随机变量： $X = 第 r 次 “ 是 ” 发生时的实验次数$

则称： $p (k) = P (X = k) = (\binom{k - 1}{r - 1}) p^{r} (1 - p)^{k - r}, k = r, r + 1, \dots$

为随机变量 X 的负二项分布，也称为帕斯卡分布，也可以记作： $X \sim N b (r, p)$

其数学期望为： $E (X) = \frac{r}{p}, V a r (X) = \frac{r (1 - p)}{p^{2}}$

负二项分布与几何分布

几何是负二项的特例：负二项分布是这样的： $p (k) = P (X = k) = (\binom{k - 1}{r - 1}) p^{r} (1 - p)^{k - r}, k = r, r + 1, \dots$ r=1 的时候，就得到了几何分布： $p (k) = P (X = k) = (1 - p)^{k - 1} p, k = 1, 2, \dots$
负二项是几何的和：参数为 r、p 的负二项分布可以表示为如下事件序列：图中所示的每一段 $X_{1} 、 X_{2} 、 \dots 、 X_{r}$ 都是几何分布，所以有： $X = X_{1} + X_{2} + \dots + X_{r} \sim N b (r, p)$ 所以负二项分布的期望为： $E (X) = E (X_{1}) + E (X_{2}) + \dots + E (X_{r}) = \frac{r}{p}$

超几何分布

设有 N 件产品，其中有 M 件不合格品，随机抽取 n 件产品，则其中含有 m 件不合格产品的概率为多少？假设随机变量： $X = 随机抽取的 n 件中有 m 件不合格品$ 这个随机变量的概率可以用古典概率来求，首先，样本空间就是从 N 件中随便抽取 n 件，所以：

$| Ω | = (\binom{N}{n})$

然后有 m 件从不合格品中抽取，剩下的在合格品中抽取，则有：

$| X | = (\binom{M}{m}) (\binom{N - M}{n - m})$

所求概率即为：

$P (X = m) = \frac{(\begin{matrix} M \\ m \end{matrix}) (\begin{matrix} N - M \\ n - m \end{matrix})}{(\begin{matrix} N \\ n \end{matrix})}, m = 0, 1, \dots, r$

其中 $r = m i n (M, n)$ 。此时称 X 服从超几何分布，可以记作：

$X \sim h (n, N, M)$

其数学期望和方差为： $E (X) = n \frac{M}{N}, V a r (X) = n \frac{M}{N} (1 - \frac{M}{N}) (1 - \frac{n - 1}{N - 1})$

超几何分布与二项分布

超几何分布与二项分布类似，都是求抽取 n 次其中有 m 次“是”的概率，只是：

二项分布：相当于抽取之后放回。
超几何分布：抽取之后不放回。

所以在超几何分布中，如果被抽取的总数 N 特别大，那么放回不放回区别也就不大了，此时，那么超几何分布可以近似看作二项分布。这点从两者的期望、方差也可以看出来： $\begin{array}{cc} 二项分布、 q q u a d & 超几何分布、 q q u a d \\ μ & n p & n \frac{M}{N} \\ σ^{2} & n p (1 - p) & n \frac{M}{N} (1 - \frac{M}{N}) (1 - \frac{n - 1}{N - 1}) \end{array}$ 令 $p = \frac{M}{N}$ ，超几何分布的期望和方差可以写作： $μ = n \frac{M}{N} = n p$ ^2=n(1-)(1-)=np(1-p)(1-) $$

对超几何分布而言，当 N 足够大的时候， $\frac{M}{N}$ 可看作取出不合格产品的概率，那此时超几何分布可看作二项分布。

总结

$\begin{array}{cc} 伯努利分布、 q u a d & 抛硬币，二选一 \\ 二项分布、 q u a d & n 重伯努利，出现 k 次 “ 是 ” \\ 泊松分布、 q u a d & 二项分布的极限 \\ 几何分布、 q u a d & n 重伯努利，第 k 次首次出现 “ 是 ” \\ 负二项分布、 q u a d & 几何分布的和 \\ 超几何分布、 q u a d & 不放回抽样的二项分布 \end{array}$

概率密度函数

如果函数 $p (x)$ 满足下列两个条件（对应了概率的三大公理）：

非负性： $p (x) \geq 0$
规范性（暗含了可加性），因为是连续的，所以通过积分相加： $\int_{- \infty}^{+ \infty} p (x) d x = 1$

则称其为概率密度函数（Probability Density Function，简写为 PDF）。

期望

离散随机变量的期望定义为： $E (X) = \sum_{i = 1}^{\infty} x_{i} p (x_{i})$

可以用类似的方法定义连续随机变量的期望，当然期望的意义是没有改变的： $E (X) = \int_{- \infty}^{+ \infty} x p (x) d x$ 关于期望的几个性质也是成立的：

复合：假设 $g (X)$ 为连续随机变量 $X$ 的某一函数，则： $E [g (X)] = \int_{- \infty}^{+ \infty} g (x) p (x) d x$
常数：若 c 为常数，则： $E (c) = c$
线性：数学期望满足：
- 齐次性，对于任意常数 a 有： $E (a X) = a E (X)$
- 可加性，对于任意两个函数 $g_{1} (X) 、 g_{2} (X)$ 有： $E [g_{1} (X) + g_{2} (X)] = E [g_{1} (X)] + E [g_{2} (X)]$

方差

方差的定义依然是： $V a r (X) = E [(X - E (X))^{2}]$

累积分布函数

连续随机变量 $X$ 的概率密度函数为 $p (x)$ ，则： $F (x) = P (X \leq x) = \int_{- \infty}^{x} p (t) d t$ 称为 $X$ 的累积分布函数。

正态分布

如果连续随机变量 $X$ 的概率密度函数为： $p (x) = \frac{1}{σ \sqrt{2 π}} e^{- \frac{(x - μ)^{2}}{2 σ^{2}}}, - \infty < x < + \infty$

则称 $X$ 服从正态分布（normal distribution），也称作高斯分布（Gaussian distribution），记作 $X \sim N (μ, σ^{2})$ ，其累积分布函数为： $F (x) = \frac{1}{σ \sqrt{2 π}} \int_{- \infty}^{x} e^{- \frac{(t - μ)^{2}}{2 σ^{2}}} d t$

我们称 $μ = 0 、 σ = 1$ 时的正态分布 $N (0, 1)$ 为标准正态分布。

期望与方差

正态分布 $X \sim N (μ, σ^{2})$ 的期望和方差为： $E (X) = μ, V a r (X) = σ^{2}$

指数分布

若随机变量 $X$ 的概率密度函数为： $p (x) = {\begin{cases} λ e^{- λ x}, & x \geq 0 \\ 0, & x < 0 \end{cases}$

其中 $λ > 0$ ，称 $X$ 服从指数分布，也可以记为： $X \sim E x p (λ)$

累积分布函数为： $F (x) = {\begin{cases} 1 - e^{- λ x}, & x \geq 0 \\ 0, & x < 0 \end{cases}$

指数分布 $X \sim E x p (λ)$ 的期望和方差为： $E (X) = \frac{1}{λ}, V a r (X) = \frac{1}{λ^{2}}$

总结

首先是一维离散随机变量的概率分布：

然后是一维连续随机变量的概率分布：

$\begin{array}{cc} 均匀分布、 q u a d & 古典派中的几何概型 \\ 正态分布、 q u a d & 二项分布的另外一种极限 \\ 指数分布、 q u a d & 泊松分布的间隔，连续的几何分布 \end{array}$

多维随机变量及其分布

联合概率质量函数

如果二维随机向量 $(X, Y)$ 所有可能的取值为 $(x_{i}, y_{j}), i, j = 1, 2, \dots$ ，这两个随机变量同时发生的概率可以用函数表示如下： $p_{i j} = P (X = x_{i}, Y = y_{j}) = P (X = x_{i} 且 Y = y_{j}), i, j = 1, 2, \dots$

且此函数满足如下性质（即概率的三大公理）：

非负性： $p_{i j} \geq 0$
规范性和可加性： $\sum_{i = 1}^{\infty} \sum_{j = 1}^{\infty} p_{i j} = 1$

则称此函数为 $(X, Y)$ 的联合概率质量函数（Joint Probability Mass Function），或者称为联合分布列，此定义可以推广到多维离散随机变量上去。

联合概率密度函数

对于某二维随机变量 $(X, Y)$ 存在二元函数 $p (x, y)$ 满足：

非负性： $p (x, y) \geq 0$
规范性和可加性（连续的都通过积分来相加）： $\int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} p (x, y) d x d y = 1$

则称此函数为 $(X, Y)$ 的联合概率密度函数（Joint Probability Density Function），此定义可以推广到多维连续随机变量上去。

联合累积分布函数

设 $(X, Y)$ 是二维随机变量，对于任意实数 $x 、 y$ ，可以定义一个二元函数来表示两个事件同时发生的概率： $F (x, y) = P ({X \leq x} 且 {Y \leq y}) = P (X \leq x, Y \leq y)$

称为二维随机变量 $(X, Y)$ 的联合累积分布函数（Joint Cumulative Distribution Function），如果混合偏导存在的话，那么：

$\frac{\partial F (x, y)}{\partial x \partial y} = p (x, y)$

得到 $p (x, y)$ 就是此分布的概率密度函数。此定义和性质可以推广到多维随机变量。

多维均匀分布

设 $D$ 为 $R^{n}$ 中的一个有界区域，其度量（直线为长度，平面为面积，空间为体积等）为 $S_{D}$ ，如果多维随机变量 $(X_{1}, X_{2}, \dots, X_{n})$ 的联合概率密度函数为： $p (x_{1}, x_{2}, \dots, x_{n}) = {\begin{cases} \frac{1}{S_{D}}, & (x_{1}, x_{2}, \dots, x_{n}) \in D \\ 0, & 其它 \end{cases}$ 则称 $(X_{1}, X_{2}, \dots, X_{n})$ 服从 $D$ 上的多维均匀分布，记作：

$(X_{1}, X_{2}, \dots, X_{n}) \sim U (D)$

边缘分布与随机变量的独立性

边缘概率质量函数

如果二维离散随机变量 $(X, Y)$ 的联合概率质量函数为： $P (X = x_{i}, Y = y_{j}), i, j = 1, 2, \dots$

对 $j$ 求和所得的函数：

$\sum_{j = 1}^{\infty} P (X = x_{i}, Y = y_{j}) = P (X = x_{i})$

称为 $X$ 的边缘概率质量函数（Marginal Probability Mass Function），或者称为边缘分布列。类似的对 i 求和所得的函数： $\sum_{i = 1}^{\infty} P (X = x_{i}, Y = y_{j}) = P (Y = y_{j})$

称为 $Y$ 的边缘概率质量函数。

边缘概率密度函数

如果二维连续随机变量 $(X, Y)$ 的联合概率密度函数为 $p (x, y)$ ，则： $p_{X} (x) = \int_{- \infty}^{+ \infty} p (x, y) d y$

称为 $X$ 的边缘概率密度函数（Marginal Probability Density Function）。类似的： $p_{Y} (y) = \int_{- \infty}^{+ \infty} p (x, y) d x$

称为 Y 的边缘概率密度函数。

边缘累积分布函数

如果二维连续随机变量 $(X, Y)$ 的联合累积分布函数为 $F (x, y)$ ，如下可以得到 $X$ 的累积分布函数： $F_{X} (x) = lim_{y \to + \infty} F (x, y) = P (X \leq x, Y < + \infty) = P (X \leq x)$

称为 $X$ 的边缘累积分布函数（Marginal Cumulative Distribution Function）。可记作： $F_{X} (x) = F (x, + \infty)$

同理可以得到 Y 的边缘累积分布函数： $F_{Y} (y) = F (+ \infty, y)$

条件分布

离散的条件分布

设 $(X, Y)$ 是二维离散型随机变量，对于固定的 $j$ ，若 $P (Y = y_{j}) \geq 0$ ，则称： $P (X = x_{i} | Y = y_{j}) = \frac{P (X = x_{i}, Y = y_{j})}{P (Y = y_{j})}, i = 1, 2, \dots$

为 $Y = y_{j}$ 条件下的随机变量 $X$ 的条件概率质量函数。同样的对于固定的 $i$ ，若 $P (X = x_{i}) \geq 0$ ，则称： $P (Y = y_{j} | X = x_{i}) = \frac{P (X = x_{i}, Y = y_{j})}{P (X = x_{i})}, j = 1, 2, \dots$

为 $X = x_{i}$ 条件下的随机变量 $Y$ 的条件概率质量函数。

条件分布和条件概率没有什么区别，一样可以用于全概率公式、贝叶斯公式。

连续的条件分布

设二维连续型随机变量 $(X, Y)$ 的概率密度函数为 $p (x, y)$ ，若对于固定的 $y$ 有边缘概率密度函数 $p_{Y} (y) > 0$ ，则： $p_{X | Y} (x | y) = \frac{p (x, y)}{p_{Y} (y)}$ 为 $Y = y$ 条件下的随机变量 $X$ 的条件概率密度函数。对应的条件累积分布函数为： $F_{X | Y} (x | y) = \int_{- \infty}^{x} \frac{p (u, y)}{p_{Y} (y)} d u$

同样的道理，以 $X = x$ 为条件有： $p_{Y | X} (y | x) = \frac{p (x, y)}{p_{X} (x)}$ F_{Y|X}(y | x)=_{-}^{y}u $$

连续的全概率和贝叶斯

全概率： $p_{Y} (y) = \int_{- \infty}^{+ \infty} p (y | x) p_{X} (x) d x$ p_{X}(x)={-}^{+} p(x | y) p{Y}(y) y $$
贝叶斯： $\begin{aligned} p (x | y) & = \frac{p (y | x) p_{X} (x)}{p_{Y} (y)} \\ = \frac{p (y | x) p_{X} (x)}{\int_{- \infty}^{+ \infty} p (y | x) p_{X} (x) d x} \end{aligned}$

多维随机变量函数的分布

随机变量的和

离散：设 X、Y 为两个相互独立的离散随机变量，取值范围为 $0 ， 1 ， 2 ， \dots$ ，则其和的概率质量函数为： $P (X + Y = k) = \sum_{i = 0}^{k} P (X = i) P (Y = k - i)$ 这个概率等式称为离散场合下的卷积公式。
连续：设 $(X, Y)$ 为二维连续型随机变量，概率密度函数为 $p (x, y)$ ，则 $Z = X + Y$ 仍为连续型随机变量，其概率密度为： $p_{X + Y} (z) = \int_{- \infty}^{+ \infty} p (z - y, y) d y = \int_{- \infty}^{+ \infty} p (x, z - x) d x$ 若 $X 、 Y$ 为相互独立，其边缘密度函数分别为 $p_{X} (x)$ 和 $p_{Y} (y)$ ，则其和 $Z = X + Y$ 的概率密度函数为： $p_{Z} (z) = \int_{- \infty}^{+ \infty} p_{X} (z - y) p_{Y} (y) d y = \int_{- \infty}^{+ \infty} p_{X} (x) p_{Y} (z - x) d x$ 上面两个概率等式称为连续场合下的卷积公式。

随机变量的数字特征

数学期望

数学期望的定义

离散随机变量的数学期望定义为： $E (X) = \sum_{i = 1}^{\infty} x_{i} p (x_{i})$

连续随机变量的数学期望定义为： $E (X) = \int_{- \infty}^{+ \infty} x p (x) d x$

函数的数学期望

一维随机变量：设 $Y$ 是随机变量 $X$ 的函数 $Y = g (X)$ (g 是连续函数）。
- 若 $X$ 为离散随机变量，则（设下式中的级数绝对收敛）： $E (Y) = E [g (X)] = \sum_{i} g (x_{i}) p (x_{i})$
- 若 $X$ 为连续随机变量，则（设下式中的积分绝对收敛）： $E (Y) = E [g (X)] = \int_{- \infty}^{+ \infty} g (x) p (x) d x$
多维随机变量：设 $Z$ 是随机变量 $(X, Y)$ 的函数 $Z = g (X, Y)$ (g 是连续函数）。
- 若 $(X, Y)$ 为离散随机变量，则（设下式中的级数绝对收敛）： $E (Z) = E [g (X, Y)] = \sum_{j} \sum_{i} g (x_{i}, y_{j}) p (x_{i}, y_{j})$
- 若 $(X, Y)$ 为连续随机变量，则（设下式中的积分绝对收敛）： $E (Z) = E [g (X, Y)] = \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} g (x, y) p (x, y) d x d y$

线性的数学期望

数学期望满足：

齐次性，对于任意常数 a 有： $E (a X) = a E (X)$
可加性，对于任意两个函数 $g_{1} (X) 、 g_{2} (X)$ 有： $E [g_{1} (X) + g_{2} (X)] = E [g_{1} (X)] + E [g_{2} (X)]$

对于多维也成立： $E (X + Y) = E (X) + E (Y)$ E(X_1+X_2++X_n)=E(X_1)+E(X_2)++E(X_n) $$

施瓦茨不等式

对任意随机变量 $X$ 与 $Y$ 都有： $[E (X Y)]^{2} \leq E (X^{2}) E (Y^{2})$

独立的数学期望

设 $(X, Y)$ 为二维独立随机变量，则有： $E (X Y) = E (X) E (Y)$ 这个结论可以推广到 n 维独立随机变量： $E (X_{1} X_{2} \dots X_{n}) = E (X_{1}) E (X_{2}) \dots E (X_{n})$

方差与标准差

方差与标准差的定义

方差定义为（因为直接通过数学期望定义的，所以没有区分离散和连续）： $V a r (X) = E [(X - E (X))^{2}]$

为了写的简单一点，也常常令 $E (X) = μ$ ，那么上式可以改写为： $V a r (X) = E [(X - μ)^{2}]$

之前也介绍过，由于方差里面含有平方，在实际应用中需要开平方才能保持单位一致，这就是标准差：

$σ (X) = \sqrt{V a r (X)}$

线性的方差

若 $a 、 b$ 为常数，则： $V a r (a X + b) = a^{2} V a r (X)$

独立的方差

设 $(X, Y)$ 为二维独立随机变量，则有： $V a r (X \pm Y) = V a r (X) + V a r (Y)$

这个结论可以推广到 n 维独立随机变量：

$V a r (X_{1} \pm X_{2} \pm \dots \pm X_{n}) = V a r (X_{1}) + V a r (X_{2}) + \dots + V a r (X_{n})$

协方差

协方差的定义

设 $(X, Y)$ 是一个二维随机变量，若 $E [(X - μ_{X}) (Y - μ_{Y})]$ 存在，则称此数学期望为 $X$ 与 $Y$ 的协方差（Covariance），记作： $C o v (X, Y) = E [(X - μ_{X}) (Y - μ_{Y})]$

特别地有 $C o v (X, X) = V a r (X)$ 。

很显然会有：

$C o v (X, Y) > 0$ 时， $X 、 Y$ 正相关，即两者有同时增加或者减少的倾向。
$C o v (X, Y) < 0$ 时， $X 、 Y$ 负相关，即两者有反向增加或者减少的倾向。
$C o v (X, Y) = 0$ 时， $X 、 Y$ 不相关，不过和独立还是有区别的，这点我们后面再论述。

协方差的性质

化简：可以通过下式来化简运算： $C o v (X, Y) = E (X Y) - E (X) E (Y)$ 据此马上可以得到一个推论： $C o v (X, Y) = C o v (Y, X)$
方差：对于任意的二维随机变量 $(X, Y)$ 有： $V a r (X + Y) = V a r (X) + V a r (Y) + 2 C o v (X, Y)$ Var(X-Y)=Var(X)+Var(Y)-2Cov(X,Y) $所以当 $ (X, Y) $ 为二维不相关随机变量时，有：$ Var(XY)=Var(X)+Var(Y) $$
分配律： $C o v (X_{1} + X_{2}, Y) = C o v (X_{1}, Y) + C o v (X_{2}, Y)$
数乘： $C o v (a X + c, b Y + d) = a b C o v (X, Y)$

独立与不相关

独立必不相关：根据刚才的性质： $C o v (X, Y) = E (X Y) - E (X) E (Y)$ 如果 X、Y 独立，则有： $E (X Y) = E (X) E (Y) ⟹ C o v (X, Y) = 0$ 所以： $独立、 i m p l i e s 不相关$
不相关不能推出独立：不相关只能说明 X、Y 之间没有正相关规律，也没有负相关规律，但可能还有很多别的规律，所以： $不相关、 / ⟹ 独立$

二维正态分布

如果二维随机变量 $(X, Y)$ 的联合概率密度函数为： $\begin{aligned} p (x, y) = & \frac{1}{2 π σ_{1} σ_{2} \sqrt{1 - ρ^{2}}} \exp {- \frac{1}{2 (1 - ρ^{2})} [\frac{{(x - μ_{1})}^{2}}{σ_{1}^{2}} \\ - \frac{2 ρ (x - μ_{1}) (y - μ_{2})}{σ_{1} σ_{2}} + \frac{{(y - μ_{2})}^{2}}{σ_{2}^{2}}]} \end{aligned}$

则称 $(X, Y)$ 服从二维正态分布，记作： $(X, Y) \sim N (μ_{1}, μ_{2}, σ_{1}^{2}, σ_{2}^{2}, ρ)$

它含有五个参数 $μ_{1} ， μ_{2} ， σ_{1}^{2} ， σ_{2}^{2}$ 和 $ρ$ ，取值范围分别为： $- \infty < μ_{1} < \infty, - \infty < μ_{2} < \infty, σ_{1} > 0, σ_{2} > 0, - 1 ⩽ ρ ⩽ 1$ 并且 $μ_{1} ， μ_{2}$ 分别是 $X 、 Y$ 的期望； $σ_{1}^{2} ， σ_{2}^{2}$ 分别是 $X 、 Y$ 的方差； $ρ$ 是 $X 、 Y$ 的相关系数。

大数定律及中心极限定理

大数定律

伯努利大数定律

整个概率论的得以存在的基础是，其所研究的随机现象虽然结果不确定，但又有规律可循。这个基础在概率论中被称为大数定律（Law of large numbers）。大数定律是一系列的定律，先来介绍伯努利大数定律：

设 $n_{A}$ 是 $n$ 次重复独立实验中事件 $A$ 发生的次数， $p$ 是事件 $A$ 在每次实验中发生的概率，则对于任意正数 $ϵ > 0$ ，有： $lim_{n \to \infty} P (| \frac{n_{A}}{n} - p | < ϵ) = 1$

或： $lim_{n \to \infty} P (| \frac{n_{A}}{n} - p | \geq ϵ) = 0$

这里需要注意不能直接用： $lim_{n \to \infty} \frac{n_{H}}{n} = p$ 而必须在外面套上一个概率函数， $\frac{n_{H}}{n}$ 并不是一个数列，而是随机变量。因此它不具备进行极限运算的前提。

依概率收敛

因为 $\frac{n_{H}}{n}$ 是随机变量，所以要表示它和 $p$ 接近，只能表示为事件： $“ 频率 P_{n} 越来越接近概率 p ” = {| \frac{n_{H}}{n} - p | < ϵ}$ 然后套上概率函数 $P$ ，对该函数求 $n$ 趋于无穷时的极限： $lim_{n \to \infty} P (| \frac{n_{H}}{n} - p | < ϵ) = 1$

这个极限同样表达了“随着 $n$ 的增大，频率 $P_{n}$ 会越来越接近概率 $p$ ”的意思，但是因为套上了概率函数，所以也称为 $P_{n}$ 依概率收敛于 $p$ ，记作： $\frac{n_{H}}{n} \overset{P}{\to} p, n \to \infty$

辛钦大数定律

伯努利大数定律局限于伯努利分布，下面介绍辛钦大数定律就没有这个限制，只是要求遵循相同的分布：设有随机变量： $X_{1}, X_{2}, \dots, X_{n}$ 这些随机变量相互独立，服从同一分布，且具有相同的数学期望： $E (X_{i}) = μ, i = 1, 2, \dots, n$ 令： $\overset{―}{X} = \frac{X_{1} + X_{2} + \dots + X_{n}}{n}$ 则对于任意 $ϵ > 0$ 有： $lim_{n \to \infty} P (| \overset{―}{X} - μ | < ϵ) = 1$ 或： $lim_{n \to \infty} P (| \overset{―}{X} - μ | \geq ϵ) = 0$ 也可以表述为： $\overset{―}{X} \overset{P}{\to} μ, n \to \infty$

切比雪夫大数定律

相同的分布也算比较严格的限制，下面介绍切比雪夫大数定律对于分布就更加宽松，只要各自的方差有共同上界即可：设有随机变量： $X_{1}, X_{2}, \dots, X_{n}$ 这些随机变量两两不相关，若每个随机变量 $X_{i}$ 的方差存在，且有共同的上界，即： $V a r (X_{i}) \leq c, i = 1, 2, \dots, n$ 令： $\overset{―}{X} = \frac{X_{1} + X_{2} + \dots + X_{n}}{n}, μ = E (\overset{―}{X})$ 则对于任意 $ϵ > 0$ 有： $lim_{n \to \infty} P (| \overset{―}{X} - μ | < ϵ) = 1$ 或： $lim_{n \to \infty} P (| \overset{―}{X} - μ | \geq ϵ) = 0$ 也可以表述为： $\overset{―}{X} \overset{P}{\to} μ, n \to \infty$

总结

这里总共介绍了三个大数定律，主要区别如下： $\begin{array}{cc} 分布、 q u a d & 独立性、 q u a d & 方差、 q u a d \\ 伯努利大数、 q u a d & 伯努利分布、 q u a d & 独立、 q u a d & 无要求、 q u a d \\ 辛钦大数 & 同分布 & 独立 & 无要求 \\ 切比雪夫大数 & 无要求 & 不相关 & 同上界、 \end{array}$

强大数定律

前面介绍的大数定律又称为弱大数定律（Weak Law of large numbers），有弱就自然就有强，下面就来介绍强大数定律（Strong Law of large numbers）：设有随机变量： $X_{1}, X_{2}, \dots, X_{n}$ 这些随机变量相互独立，服从同一分布，且具有相同的数学期望： $E (X_{i}) = μ, i = 1, 2, \dots, n$ 令： $\overset{―}{X} = \frac{X_{1} + X_{2} + \dots + X_{n}}{n}$ 则对于任意 $ϵ > 0$ 有： $P (lim_{n \to \infty} | \overset{―}{X} - μ | < ϵ) = 1$ 或： $P (lim_{n \to \infty} | \overset{―}{X} - μ | \geq ϵ) = 0$

这个强大数定律和之前的辛钦大数定律非常接近：

弱大数定律（辛钦大数定律），极限符号在 P 函数外面： $lim_{n \to \infty} P (| \overset{―}{X} - μ | < ϵ) = 1$
强大数定律，极限符号在 P 函数里面： $P (lim_{n \to \infty} | \overset{―}{X} - μ | < ϵ) = 1$ 仔细体会这两则之间的区别^ _ ^。

中心极限定理

棣莫弗-拉普拉斯定理

设随机变量 $X \sim b (n, p)$ ，则对任意 x 有： $lim_{n \to \infty} P (\frac{X - n p}{\sqrt{n p (1 - p)}} \leq x) = Φ (x) = \frac{1}{\sqrt{2 π}} \int_{- \infty}^{x} e^{- \frac{t^{2}}{2}} d t$

林德伯格-莱维定理

设随机变量： $X_{i}, i = 1, 2, \dots, n$ 相互独立，服从同一分布，且有相同的数学期望和方差： $E (X_{i}) = μ, V a r (X_{i}) = σ^{2}$ 则随机变量： $Y = \frac{X_{1} + X_{2} + \dots + X_{n} - n μ}{σ \sqrt{n}}$ 对于任意实数 $y$ 有： $lim_{n \to \infty} F_{Y} (y) = lim_{n \to \infty} P (Y \leq y) = Φ (y) = \frac{1}{\sqrt{2 π}} \int_{- \infty}^{y} e^{- \frac{t^{2}}{2}} d t$

参考文献

《马同学的概率论与数理统计》
感兴趣的可以购买他的课程，写的很好（强烈推荐）！！！