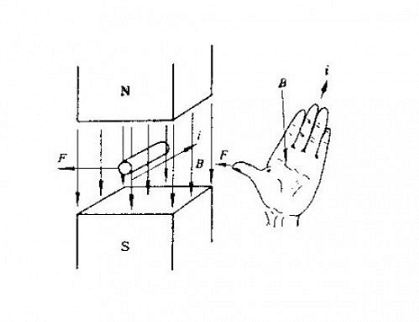
将左手的食指,中指和拇指伸直,使其在空间内相互垂直。食指方向代表磁场的方向(从 N 级到 S 级),中指代表电流的方向(从正极到负极),那拇指所指的方向就是受力的方向。可用于判断安培力(运动导体所受到的力)和洛伦兹力(运动电荷所受的力)。
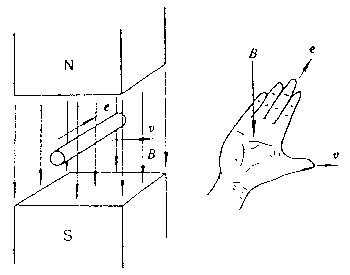
伸开右手,使拇指与其余四个手指垂直,并且都与手掌在同一平面内;让磁感线垂直于手心进入,并使拇指指向导线运动方向,这时四指所指的方向就是感应电流的方向。用于判断导体在做切割磁场时产生的电流方向。
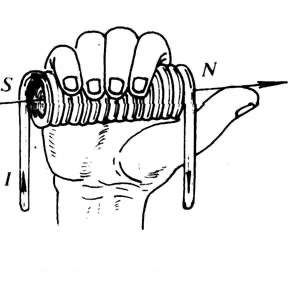
电直导线中的安培定则(安培定则一):用右手握住通电直导线,让大拇指指向直导线中电流方向,那么四指指向就是通电导线周围磁场的方向;
安培力: 以电流强度为 I 的长度为 L 的直导线,置于磁感应强度为 B 的均匀外磁场中,则导线受到的安培力的大小为:
F = I B L s i n α F = IBLsin\alpha
F = I B L s i n α
式中α为导线中的电流方向与 B 方向之间的夹角。f m f_m f m
f m = μ 0 I 1 I 2 2 π r f_m = \frac{\mu_0 I_1 I_2 }{2\pi r}
f m = 2 π r μ 0 I 1 I 2
其中,μ 0 \mu_{0} μ 0 I 1 , I 2 I_1,I_2 I 1 , I 2 μ 0 \mu_{0} μ 0
μ 0 = 4 π × 1 0 − 7 \mu _{0} = 4\pi \times 10^{-7}
μ 0 = 4 π × 1 0 − 7
长直载流导线周围的磁感应强度大小与距离成反比、与电流成正比。
d B = μ 0 4 π I d l s i n θ r 2 dB = \frac{\mu _0}{4\pi} \frac{Idl sin\theta }{r^2}
d B = 4 π μ 0 r 2 I d l s i n θ
真空磁导率:
μ 0 = 4 π × 1 0 − 7 N ⋅ A − 2 \mu _0 = 4 \pi \times 10^{-7} N \cdot A^{-2}
μ 0 = 4 π × 1 0 − 7 N ⋅ A − 2
载流直导线、圆形载流导线、载流密绕直螺线管的磁场都是通过该公式求取。具体细节可参考 毕奥─萨伐尔定律
在电动力学里,若考虑一带电粒子在电磁场中的受力,可以用以下的劳仑兹力定律表示:
F = q ( E + v × B ) F = q(E + v \times B)
F = q ( E + v × B )
这里 F 是洛伦兹力,q 是是带电粒子的电荷量,E 是电场,v 是带电粒子的速度,B 是磁场。这方程式右边有两项,第一项是电场力F E = q E F_E = qE F E = q E F B = q v × B F_B = qv \times B F B = q v × B
若电枢导体的有效长度为 l,导体切割气隙磁场的线速度为 v,则每根导体中的感应电动势e c e_c e c
e c = b σ l v e_c = b_{\sigma}lv
e c = b σ l v
式中b σ b_{\sigma} b σ Z a Z_a Z a Z a 2 a \frac{Z_a}{2a} 2 a Z a E a E_a E a
E a = ∑ 1 Z a 2 a b δ l v = l v ∑ 1 Z a 2 a b δ ( x i ) E_a = \sum_{1}^{\frac{Z_a}{2a}}b_{\delta }lv = lv\sum_{1}^{\frac{Z_a}{2a}}b_{\delta }(x_i)
E a = 1 ∑ 2 a Z a b δ l v = l v 1 ∑ 2 a Z a b δ ( x i )
式中各点气隙磁通密度b δ ( x i ) b_{\delta }(x_i) b δ ( x i ) B a v B_{av} B a v
B a v ≈ 1 Z a 2 a ∑ 1 Z a 2 a b δ ( x i ) B_{av} \approx \frac{1}{\frac{Z_a}{2a}} \sum_{1}^{\frac{Z_a}{2a}}b_{\delta }(x_i)
B a v ≈ 2 a Z a 1 1 ∑ 2 a Z a b δ ( x i )
则E a E_a E a
E a = l v Z a 2 a B a v E_a = lv\frac{Z_a}{2a}B_{av}
E a = l v 2 a Z a B a v
考虑到线速度v = 2 p τ n 60 v = 2p \tau \frac{n}{60} v = 2 p τ 6 0 n τ \tau τ
E a = 2 p n 60 Z a 2 a ( B a v τ l ) = p Z a 60 a n Φ = C e n Φ E_a = 2\frac{pn}{60}\frac{Z_a}{2a}(B_{av}\tau l) = \frac{pZ_a}{60a}n\Phi = C_e n \Phi
E a = 2 6 0 p n 2 a Z a ( B a v τ l ) = 6 0 a p Z a n Φ = C e n Φ
式中Φ \Phi Φ B a v B_av B a v l τ l\tau l τ C e C_e C e C e = p Z a 60 a C_e = \frac{p Z_a}{60a} C e = 6 0 a p Z a
设导体中电流为i a i_a i a b δ b_{\delta} b δ T c T_c T c
T c = b δ l i a D a 2 T_c = b_{\delta} l i_a \frac{D_a}{2}
T c = b δ l i a 2 D a
D a D_a D a Z a 2 p \frac{Z_a}{2p} 2 p Z a T p T_p T p
T p = l i a D a 2 ∑ 1 Z a 2 p b δ ( x i ) = ( Z a 2 p B a v ) l i a D a 2 T_p = li_a \frac{D_a}{2}\sum_{1}^{\frac{Z_a}{2p}}b_{\delta }(x_i) = (\frac{Z_a}{2p}B_{av})li_a\frac{D_a}{2}
T p = l i a 2 D a 1 ∑ 2 p Z a b δ ( x i ) = ( 2 p Z a B a v ) l i a 2 D a
式中B a v B_{av} B a v T e T_e T e T p T_p T p
T e = 2 p T p = Z a B a v l i a D a 2 T_e = 2pT_p = Z_aB_{av}li_a \frac{D_a}{2}
T e = 2 p T p = Z a B a v l i a 2 D a
考虑到π D a = 2 p τ , Φ = B a v l τ \pi D_a = 2p\tau , \Phi = B_{av}l \tau π D a = 2 p τ , Φ = B a v l τ i a = I a 2 a i_a = \frac{I_a}{2a} i a = 2 a I a I a I_a I a
T e = Z a B a v l ( I a 2 a ) p τ π = p 2 π Z a a Φ I a = C T Φ I a T_e = Z_aB_{av}l(\frac{I_a}{2a}) \frac{p \tau}{\pi} = \frac{p}{2\pi} \frac{Z_a}{a} \Phi I_a = C_T \Phi I_a
T e = Z a B a v l ( 2 a I a ) π p τ = 2 π p a Z a Φ I a = C T Φ I a
式中C T C_T C T
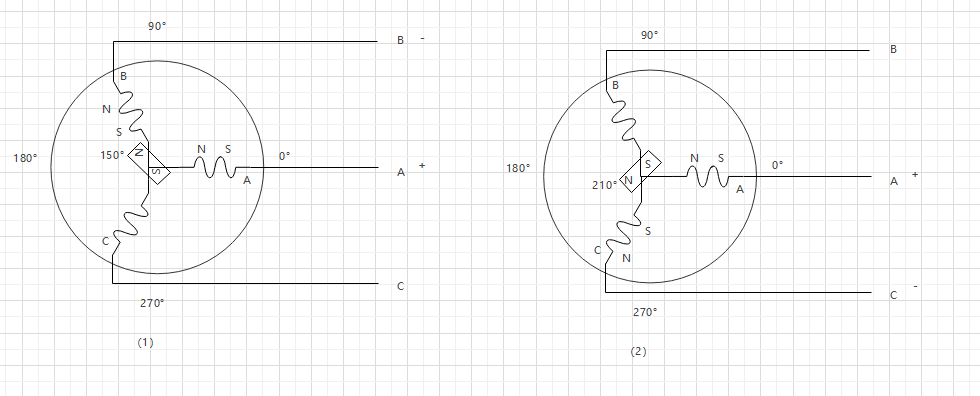
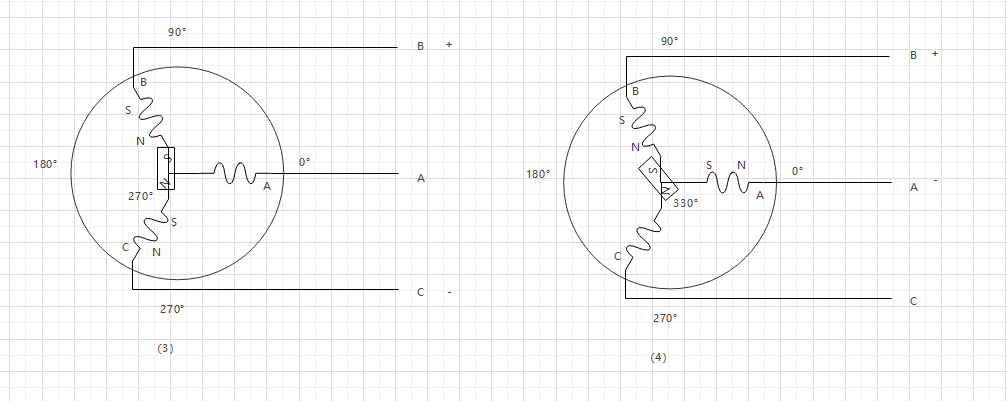
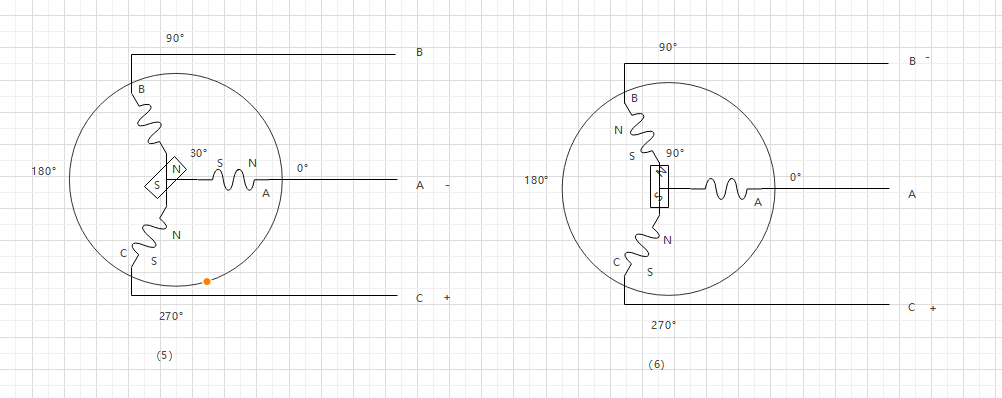
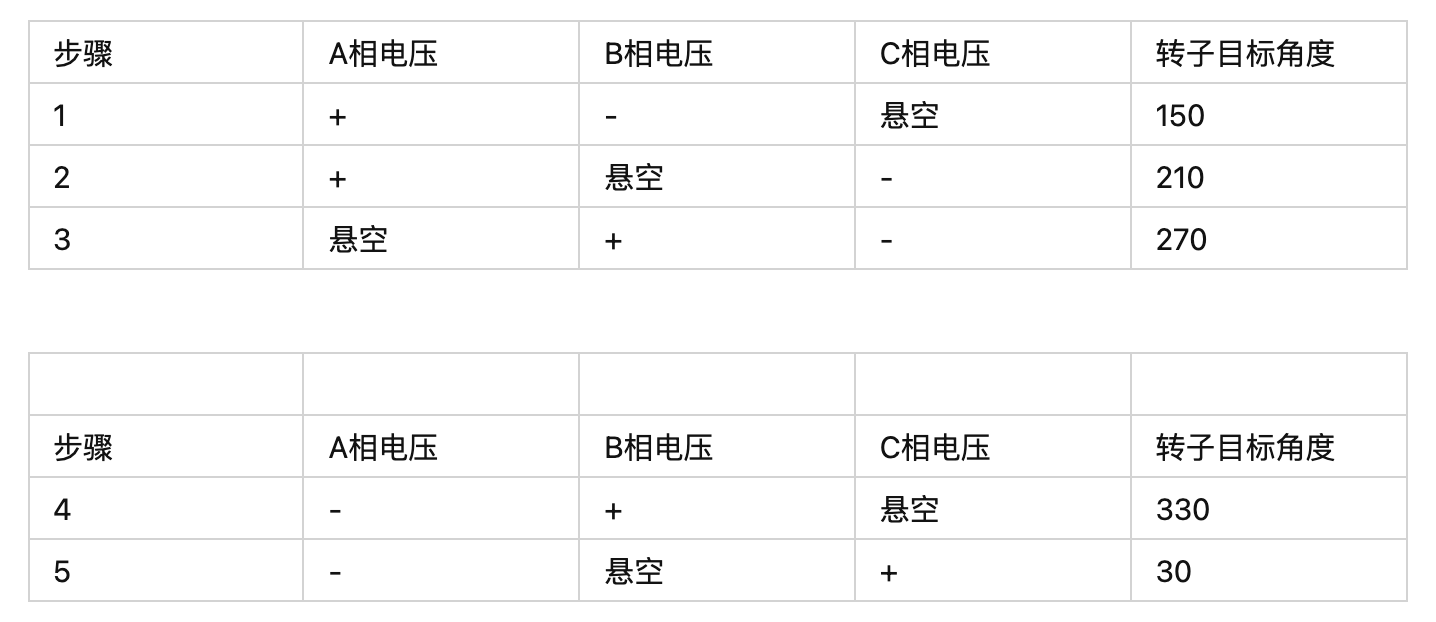
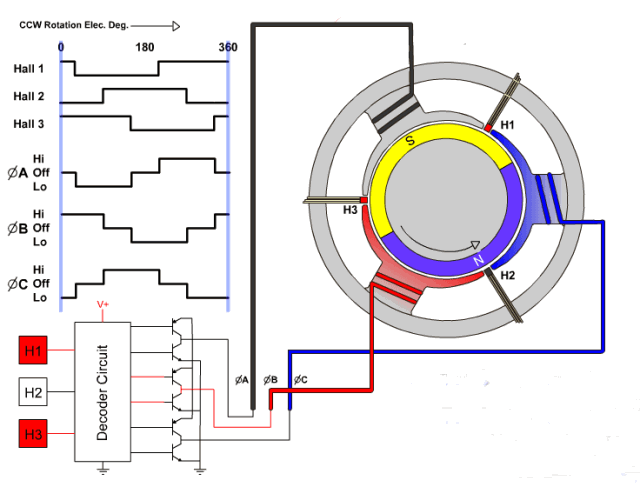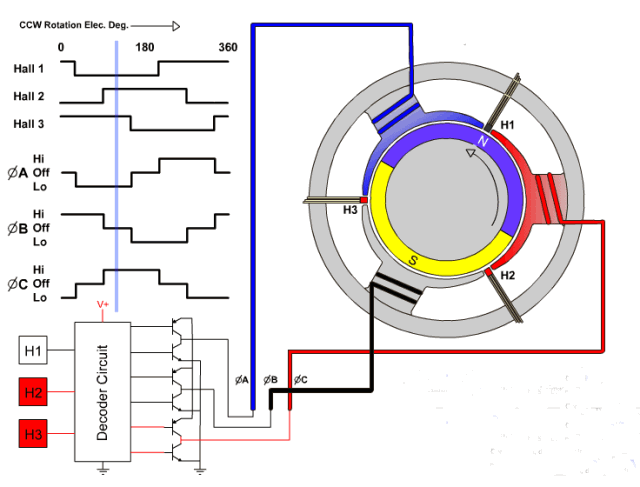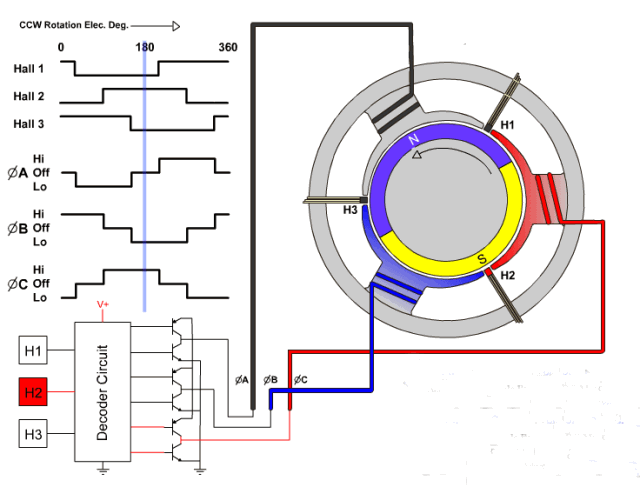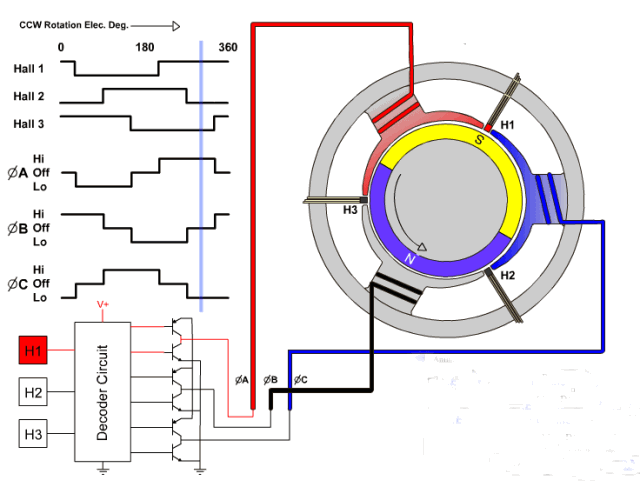
采用动图表示如下:
BLDC 的六步方波控制参考 BLDC 的六步方波控制
BLDC 就是通过三相进行改变线圈的电流方向来改变磁场方向,从而免去使用换向器来提高电机的性能,以上是 bldc 的六步控制法,
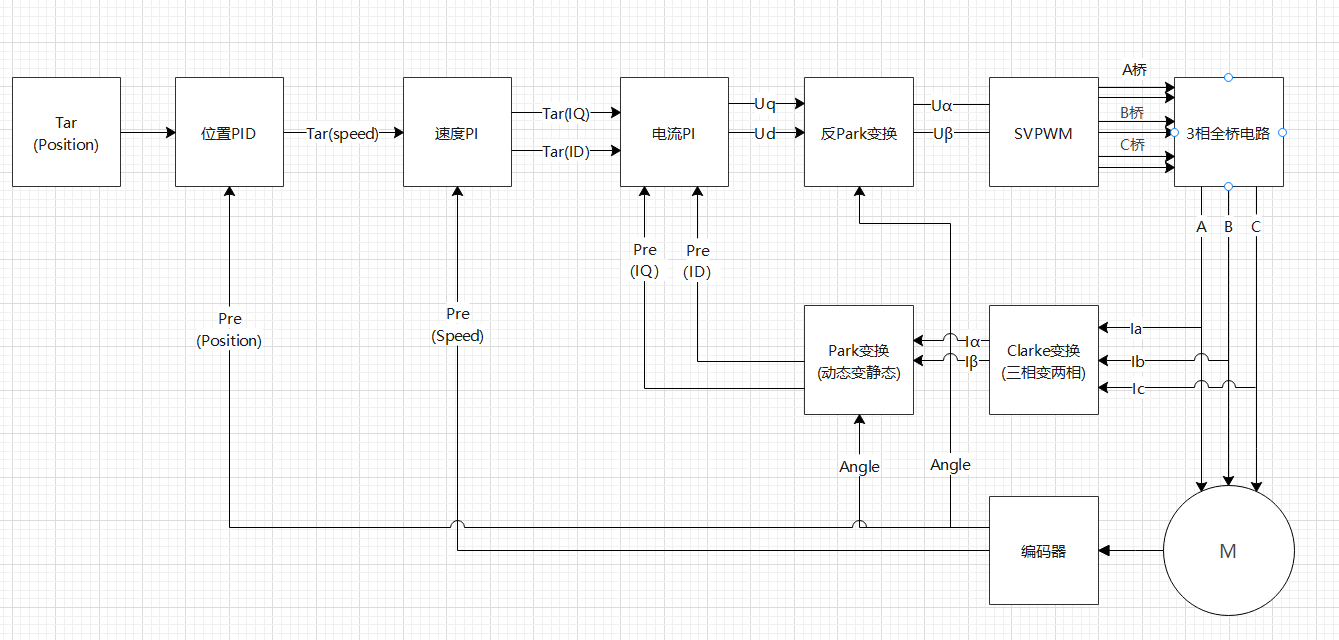
这里先将 FOC 控制框图列出,在下面将会一个模块一个模块当介绍。
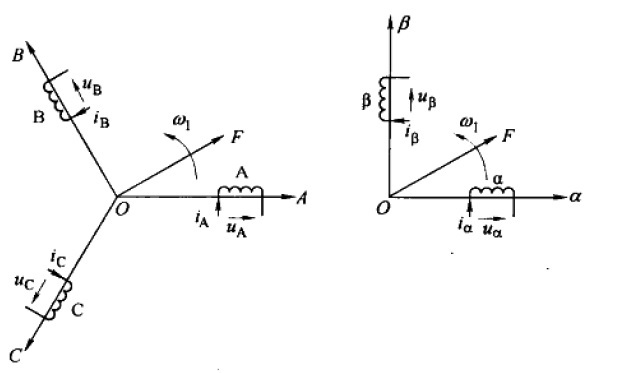
在上图中 clark 变换是将I a I b I c I_a I_b I_c I a I b I c I α I β I_{\alpha} I_{\beta} I α I β
I α = I a − c o s ( π 3 ) I b − c o s ( 2 π 3 ) I c I β = s i n ( π 3 ) I b − s i n ( π 3 ) I c \begin{aligned}
&I_{\alpha } = I_a - cos(\frac{\pi }{3})I_b - cos(\frac{2\pi }{3})I_c \\
&I_{\beta } = sin(\frac{\pi }{3})I_b - sin(\frac{\pi }{3})I_c
\end{aligned}
I α = I a − c o s ( 3 π ) I b − c o s ( 3 2 π ) I c I β = s i n ( 3 π ) I b − s i n ( 3 π ) I c
写成矩阵形式如下:
[ I α I β ] = [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] [ I a I b I c ] \begin{bmatrix} I_{\alpha }\\ I_{\beta } \end{bmatrix} = \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} I_a\\
I_b\\ I_c\end{bmatrix}
[ I α I β ] = [ 1 0 − 2 1 2 3 − 2 1 − 2 3 ] ⎣ ⎢ ⎡ I a I b I c ⎦ ⎥ ⎤
但是到这里还没完,我们在实际使用过程中使用的公司并不是这个而是有一个系数 k 来调整为等幅变换或等功率变换,实际使用的公式如下:
[ I α I β ] = k ∗ [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] [ I a I b I c ] \begin{bmatrix} I_{\alpha }\\ I_{\beta } \end{bmatrix} = k * \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} I_a\\
I_b\\ I_c\end{bmatrix}
[ I α I β ] = k ∗ [ 1 0 − 2 1 2 3 − 2 1 − 2 3 ] ⎣ ⎢ ⎡ I a I b I c ⎦ ⎥ ⎤
在等幅值变换中k = 2 3 k = \frac{2}{3} k = 3 2
以相电压来作为推导而不是相电流,设V m V_m V m
U a = V m ∗ c o s ( θ ) U b = V m ∗ c o s ( θ − 2 π 3 ) U c = V m ∗ c o s ( θ + 2 π 3 ) U a + U b + U c = 0 \begin{aligned}
&U_a = V_m * cos(\theta) \\
&U_b = V_m * cos(\theta - \frac{2\pi }{3}) \\
&U_c = V_m * cos(\theta + \frac{2\pi }{3}) \\
&U_a + U_b + U_c = 0
\end{aligned}
U a = V m ∗ c o s ( θ ) U b = V m ∗ c o s ( θ − 3 2 π ) U c = V m ∗ c o s ( θ + 3 2 π ) U a + U b + U c = 0
这里θ = 2 π f t \theta = 2\pi ft θ = 2 π f t U t U_t U t
U t = U a + U b ∗ e 2 π j 3 + U c ∗ e 4 π j 3 = 3 2 V m ∗ e j θ U_t = U_a + U_b * e^{\frac{2 \pi j}{3}} + U_c * e^{\frac{4 \pi j}{3}} = \frac{3}{2}V_m * e^{j\theta }
U t = U a + U b ∗ e 3 2 π j + U c ∗ e 3 4 π j = 2 3 V m ∗ e j θ
由此可以看出合成的电压矢量是原来的3 2 \frac{3}{2} 2 3 k = 2 3 k = \frac{2}{3} k = 3 2 k = 2 3 k = \frac{2}{3} k = 3 2
U α = U a U β = 1 3 ( U a + 2 U b ) \begin{aligned}
&U_{\alpha } = U_a \\
&U_{\beta } = \frac{1}{\sqrt{3}}(U_a + 2U_b)
\end{aligned}
U α = U a U β = 3 1 ( U a + 2 U b )
另一种变换是等功率变换,当k = 2 3 k = \sqrt{\frac{2}{3}} k = 3 2 Clark 变换及比例系数 2/3 推导过程
关于电流采样参考 [[FOCCurrentSampling]]
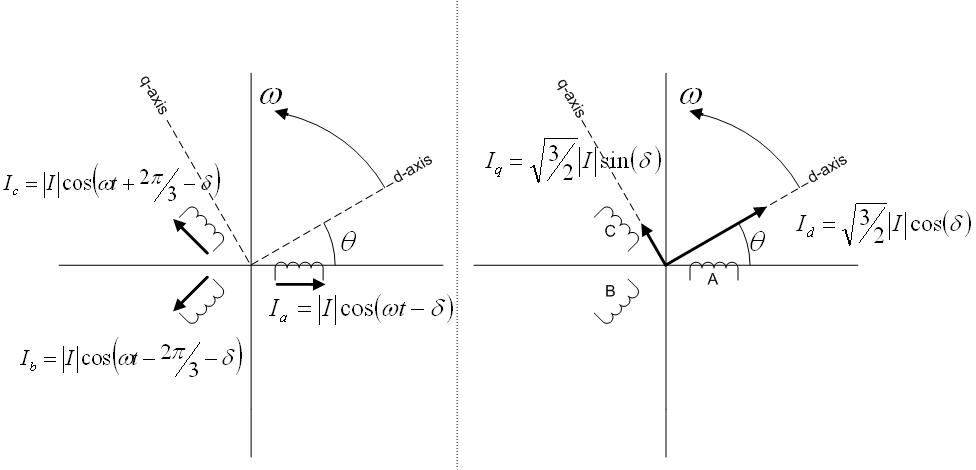
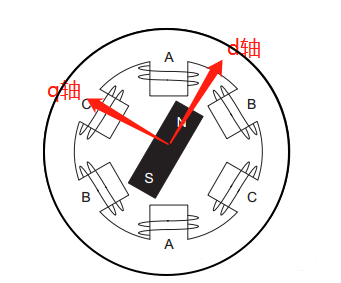
dq 坐标系是建立在转子上的直角坐标系,其中:
d 轴方向与转子磁链方向重合,又叫直轴;
d 轴和𝑞轴 q 轴如下图所示;
相对与定子来说是旋转的坐标系,在 dq 坐标系下i d i q i_d i_q i d i q
i d = i α ∗ c o s ( θ ) + i β ∗ s i n ( θ ) i q = − i α ∗ s i n ( θ ) + i β ∗ c o s ( θ ) \begin{aligned}
&i_d = i_{\alpha} * cos(\theta) + i_{\beta} * sin(\theta) \\
&i_q = -i_{\alpha} * sin(\theta) + i_{\beta} * cos(\theta)
\end{aligned}
i d = i α ∗ c o s ( θ ) + i β ∗ s i n ( θ ) i q = − i α ∗ s i n ( θ ) + i β ∗ c o s ( θ )
写成矩阵式为:
[ i d i q ] = [ c o s ( θ ) s i n ( θ ) − s i n ( θ ) c o s ( θ ) ] [ i α i β ] \begin{bmatrix}i_d\\ i_q\end{bmatrix} = \begin{bmatrix}cos(\theta ) & sin(\theta )\\ -sin(\theta ) & cos(\theta )\end{bmatrix}\begin{bmatrix}i_{\alpha }\\ i_{\beta }\end{bmatrix}
[ i d i q ] = [ c o s ( θ ) − s i n ( θ ) s i n ( θ ) c o s ( θ ) ] [ i α i β ]
通过 park 变换后将交流信号转变为直流信号,这样就方便进行信号调节,像使用 pid 控制器对电机信号进行控制。
Park 反变换又叫直交变换,由 dq 轴的直流量,最终变换到αβ的交流量,其公式如下:
i α = i d ∗ c o s ( θ ) − i q ∗ s i n ( θ ) i α = i d ∗ s i n ( θ ) + i q ∗ c o s ( θ ) \begin{aligned}
&i_{\alpha} = i_d * cos(\theta) - i_q * sin(\theta) \\
&i_{\alpha} = i_d * sin(\theta) + i_q * cos(\theta)
\end{aligned}
i α = i d ∗ c o s ( θ ) − i q ∗ s i n ( θ ) i α = i d ∗ s i n ( θ ) + i q ∗ c o s ( θ )
写成矩阵形式如下:
[ i α i β ] = [ c o s ( θ ) − s i n ( θ ) s i n ( θ ) c o s ( θ ) ] [ i d i q ] \begin{bmatrix}i_{\alpha }\\ i_{\beta }\end{bmatrix} = \begin{bmatrix}cos(\theta ) & -sin(\theta )\\ sin(\theta ) & cos(\theta )\end{bmatrix}\begin{bmatrix}i_d\\ i_q\end{bmatrix}
[ i α i β ] = [ c o s ( θ ) s i n ( θ ) − s i n ( θ ) c o s ( θ ) ] [ i d i q ]
因为 svpwm 使用的坐标系还是αβ坐标系,在经过 park 变换后进行调控例如使用 pid 控制器对其中的参数进行调控后需要再经过反 park 变换回去输入到 svpwn 模块中去。
这里需要注意 park 变换是需要电角度信息的,因此这里涉及无感和有感两种 foc,由于本人也没有研究过无感 foc 因此这里只讲下有感 foc。所谓有感就是有传感器,通过传感器获得电机转子的位置,传感器种类很多有光电式和霍尔传感器式,按照获取角度类型可以分为绝对式编码器和相对式编码器,但无论哪种传感器最终都是获得电机转子的位置,然后在 park 变换的时候用于将α β \alpha \beta α β
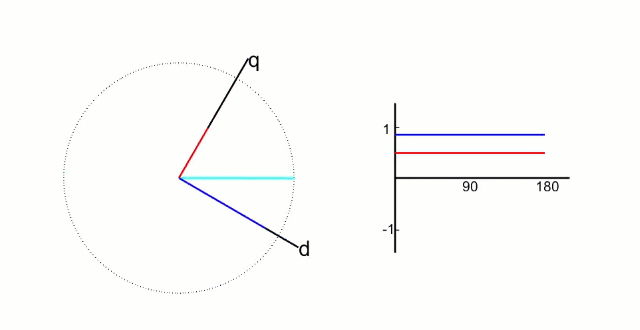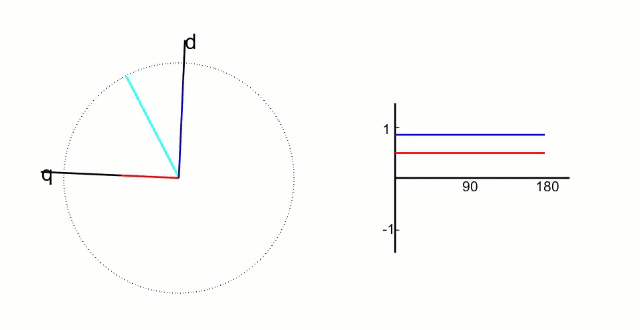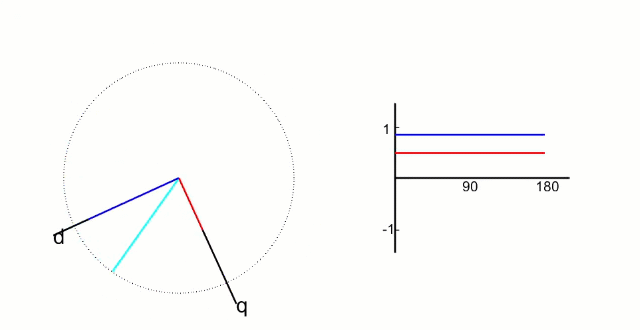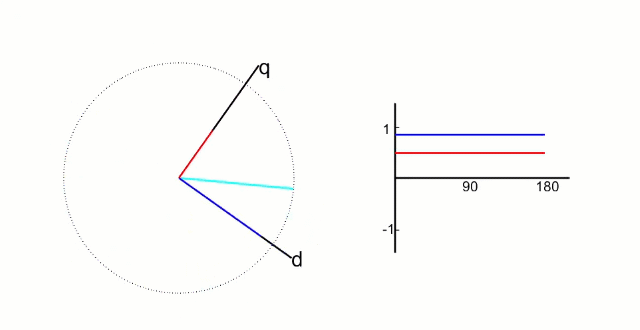
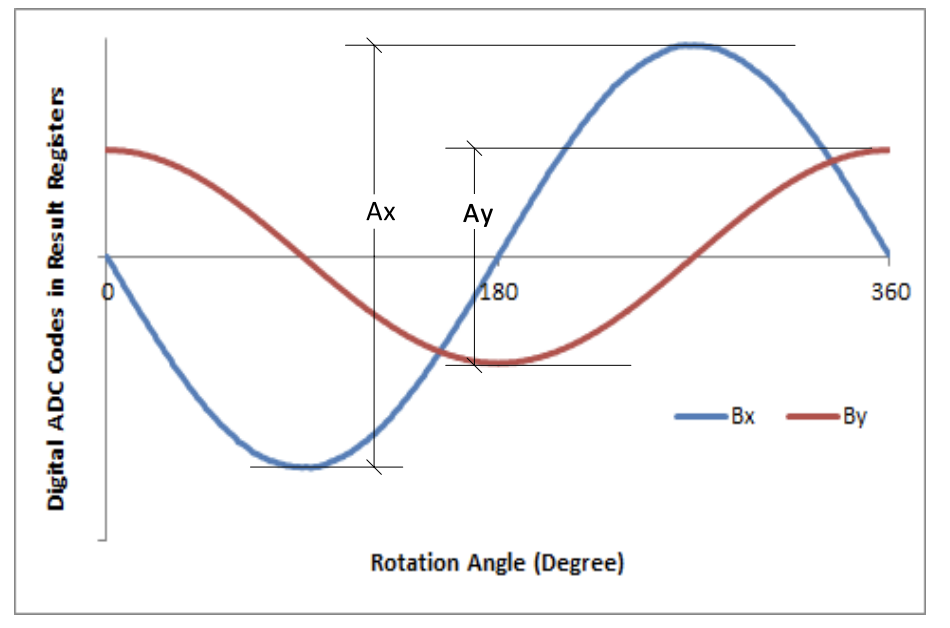
两个呈 90 摆放的 drv5055 传感器在电机转子旋转一周输出的波形如上图所示,这里主要说明两点:
使用呈 90 度摆放的两个传感器的好处:单个传感器以上图B x B_x B x
关于传感器校准,从上图可以看到两个传感器的幅值不同,一般情况下都是不同的,两个传感器不可能做的完全一样而且安装也会又偏差,因此需要对传感器进行校准,校准方法就是对两个传感器进行归一化处理,分别找到两个传感器对极值进而就确定了中值(理想情况下中值为 0 但实际上往往存在偏差)将其归一化到 [-1, 1] 这个值域内就完成了对传感器对校准。
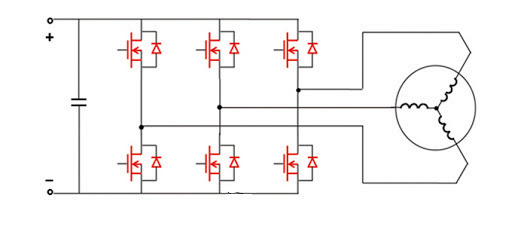
SVPWM 是近年发展的一种比较新颖的控制方法,是由三相功率逆变器的六个功率开关元件组成的特定开关模式产生的脉宽调制波,能够使输出电流波形尽 可能接近于理想的正弦波形。空间电压矢量 PWM 与传统的正弦 PWM 不同,它是从三相输出电压的整体效果出发,着眼于如何使电机获得理想圆形磁链轨迹。 SVPWM 技术与 SPWM 相比较,绕组电流波形的谐波
SVPWM 的理论基础是平均值等效原理,即在一个开关周期内通过对基本电压矢量加以组合,使其平均值与给定电压矢量相等。在某个时刻,电压矢量旋转到某个区域中,可由组成这个区域的两个相邻的非零矢量和零矢量在时间上的不同组合来得到。两个矢量的作用时间在一个采样周期内分多次施加,从而控制各个电压矢量的作用时间,使电压空间矢量接近按圆轨迹旋转,通过逆变器的不同开关状态所产生的实际磁通去逼近理想磁通圆,并由两者的比较结果来决定逆变器的开关状态,从而形成 PWM 波形。
S x = { 1 (上桥臂导通) 0 (下桥臂导通) S_x = \left\{\begin{matrix}
1(上桥臂导通)\\
0(下桥臂导通)
\end{matrix}\right.
S x = { 1 ( 上 桥 臂 导 通 ) 0 ( 下 桥 臂 导 通 )
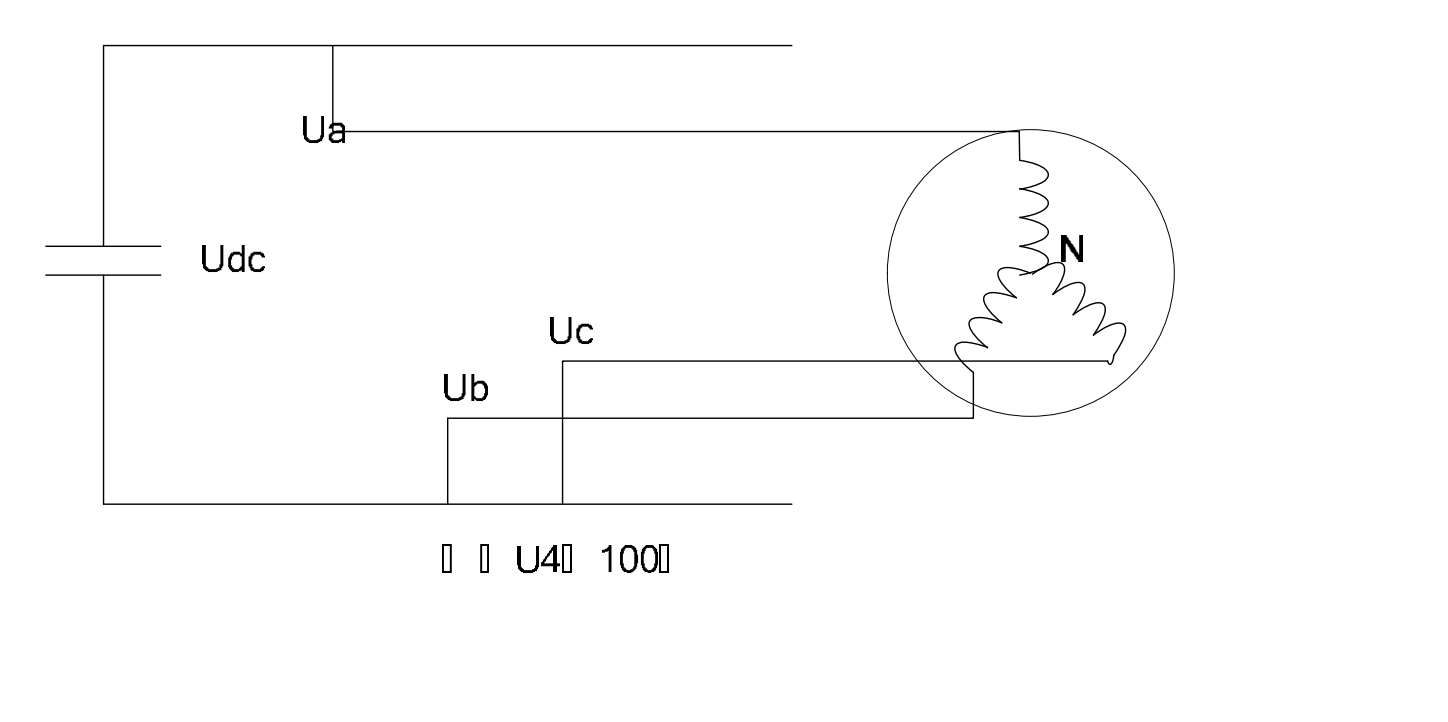
(Sa、Sb、Sc) 的全部可能组合共有八个,包括 6 个非零矢量 Ul(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)、和两个零矢量 U0(000)、U7(111),下面以其中一 种开关组合为例分析,假设 Sx ( x= a、b、c)= (100), 此时:
U a b = U d c , U b c = 0 , U c a = − U d c U a N − U b N = U d c , U a N − U c N = U d c U a N + U b N + U c N = 0 \begin{aligned}
&U_{ab} = U_{dc}, U_{bc} = 0, U_{ca} = -U_{dc} \\
&U_{aN} - U_{bN} = U_{dc},U_{aN} - U_{cN} = U_{dc} \\
&U_{aN} + U_{bN} + U_{cN} = 0
\end{aligned}
U a b = U d c , U b c = 0 , U c a = − U d c U a N − U b N = U d c , U a N − U c N = U d c U a N + U b N + U c N = 0
求解上述方程可得:
U a N = 2 U d 3 U b N = − U d 3 U c N = − U d 3 \begin{aligned}
&U_{aN} = \frac{2U_d}{3} \\
&U_{bN} = - \frac{U_d}{3} \\
&U_{cN} = - \frac{U_d}{3}
\end{aligned}
U a N = 3 2 U d U b N = − 3 U d U c N = − 3 U d
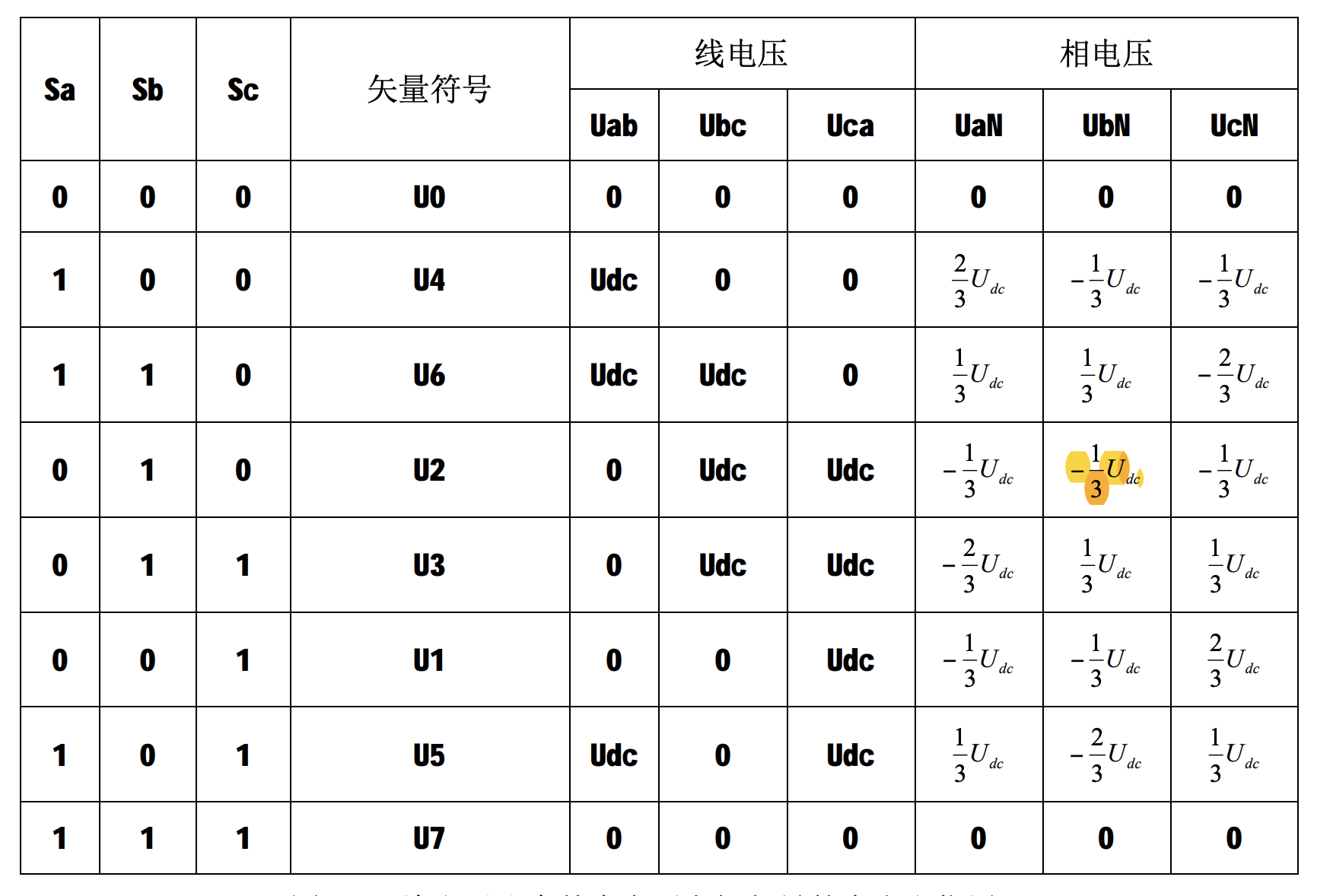
同理可计算出其它各种组合下的空间电压矢量,列表如下:
其中非零矢量的幅值相同(模长为 2 U d c 3 \frac{2U_{dc}}{3} 3 2 U d c
∫ 0 T U r e f d t = ∫ 0 T x U x d t + ∫ T x T x + T y U y d t + ∫ T x + T y T U 0 d t \int_{0}^{T}U_{ref} dt = \int_{0}^{T_x}U_x dt + \int_{T_x}^{T_x + T_y}U_y dt + \int_{T_x + T_y}^{T}U_0 dt
∫ 0 T U r e f d t = ∫ 0 T x U x d t + ∫ T x T x + T y U y d t + ∫ T x + T y T U 0 d t
等效与下式:
U r e f ∗ T = U x ∗ T x + U y ∗ T y + U 0 ∗ T 0 U_{ref} * T = U_x * T_x + U_y * T_y + U_0 * T_0
U r e f ∗ T = U x ∗ T x + U y ∗ T y + U 0 ∗ T 0
其中,U r e f U_{ref} U r e f T x 、 T y 、 T 0 T_x、T_y、T_0 T x 、 T y 、 T 0 U x 、 U y U_x、U_y U x 、 U y U 0 U_0 U 0 U 0 U_0 U 0 U 0 U_0 U 0 U 7 U_7 U 7 U r e f U_{ref} U r e f U x 、 U y 、 U 0 U_x、U_y、U_0 U x 、 U y 、 U 0 T x 、 T y 、 T 0 T_x、T_y、T_0 T x 、 T y 、 T 0
三相电压给定所合成的电压向量旋转角速度为ω=2πf,旋转一周所需的时间为 T =1/f ;若载波频率是 fs,则频率比为 R = fs / f。这样将电压旋转平面等切割成 R 个小增量,亦 即设定电压向量每次增量的角度是 :
γ = 2 R = 2 π f f s = 2 T s T \gamma = \frac{2}{R} = \frac{2 \pi f}{fs} = \frac{2Ts}{T}
γ = R 2 = f s 2 π f = T 2 T s
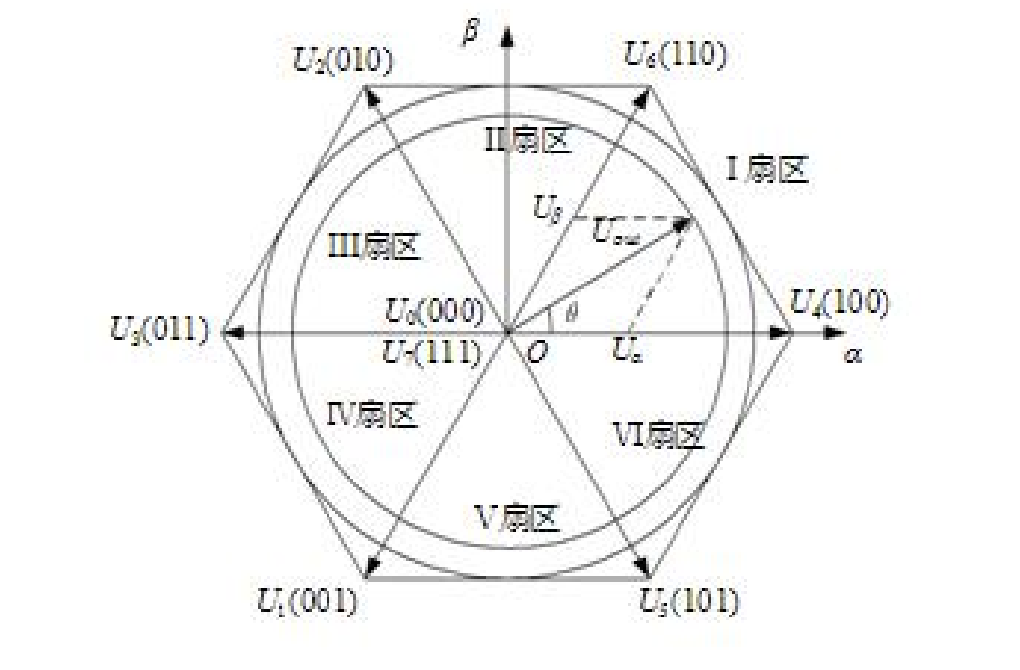
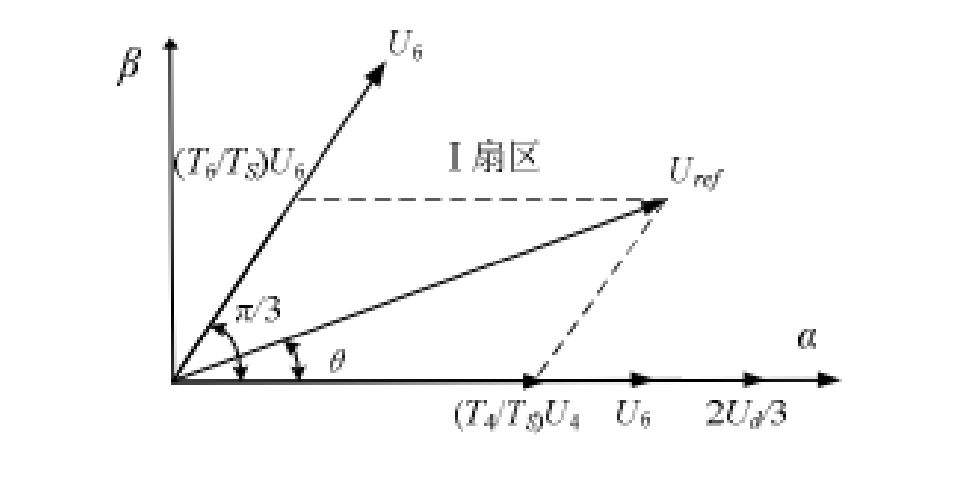
假设欲合成的电压向量 U r e f U_{ref} U r e f U r e f ∗ T z = U 4 ∗ T 4 + U 6 ∗ T 6 U_ref * Tz =U4 * T4 +U6 * T6 U r e f ∗ T z = U 4 ∗ T 4 + U 6 ∗ T 6
在两相静止参考坐标系(α,β)中,令U r e f U_{ref} U r e f
∣ U r e f ∣ c o s ( θ ) = T 4 T s ∣ U 4 ∣ + T 6 T s ∣ U 6 ∣ c o s ( π 3 ) ∣ U r e f ∣ s i n ( θ ) = T 6 T s ∣ U 6 ∣ s i n ( π 3 ) \left | U_{ref} \right | cos(\theta ) = \frac{T_4}{T_s}\left | U_4 \right | + \frac{T_6}{T_s} \left | U_6 \right | cos(\frac{\pi }{3})\\
\left | U_{ref} \right | sin(\theta ) = \frac{T_6}{T_s} \left | U_6 \right | sin(\frac{\pi }{3})
∣ U r e f ∣ c o s ( θ ) = T s T 4 ∣ U 4 ∣ + T s T 6 ∣ U 6 ∣ c o s ( 3 π ) ∣ U r e f ∣ s i n ( θ ) = T s T 6 ∣ U 6 ∣ s i n ( 3 π )
因为 |U4 |=|U6|=2Udc/3 ,所以可以得到各矢量的状态保持时间为:
T 4 = m T s s i n ( π 3 − θ ) T 6 = m T s s i n ( θ ) \begin{aligned}
&T_4 = mT_s sin(\frac{\pi }{3} - \theta ) \\
&T_6 = mT_s sin(\theta )
\end{aligned}
T 4 = m T s s i n ( 3 π − θ ) T 6 = m T s s i n ( θ )
式中 m 为 SVPWM 调制系数(调制比), m = 3 ∣ U r e f ∣ U d c m= \frac{\sqrt{3}\left | U_{ref} \right |}{U_{dc}} m = U d c 3 ∣ U r e f ∣
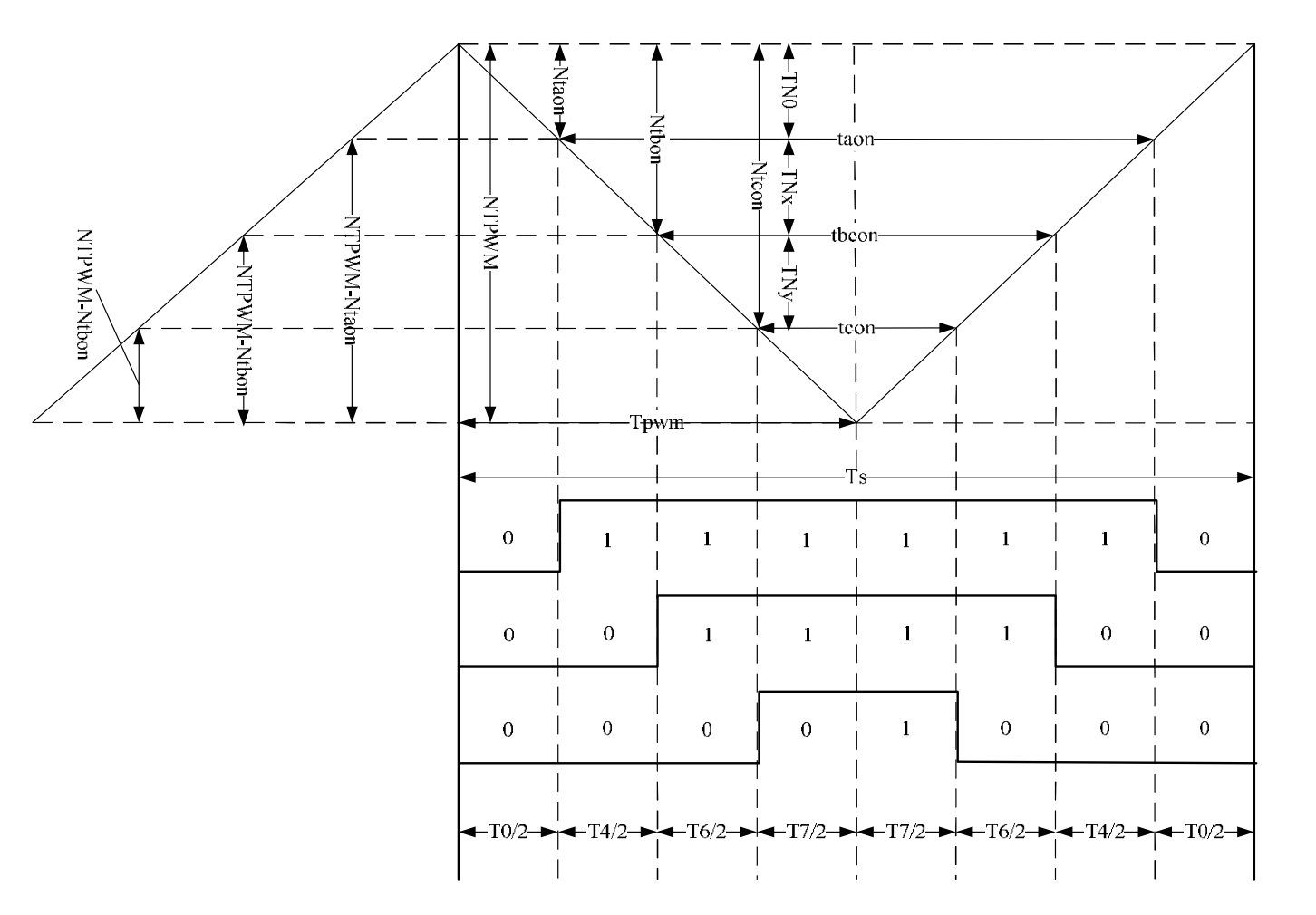
我们以减少开关次数为目标,将基本矢量作用顺序的分配原则选定为:在每次开关状态转换时,只改变其中一相的 开关状态。并且对零矢量在时间上进行了平均分配,以使产生的 PWM 对称,从而有效地降低 PWM 的谐波分量。当 U4(100) 切换至 U0(000) 时,只需改变 A 相上下一对切换开关,若由 U4(100) 切换至 U7(111) 则需改变 B、C 相上下两对切换开关,增加了一倍的切换损失。因此要改变电压向量 U4(100)、U2(010)、 U1(001) 的大小,需配合零电压向量 U0(000),而要改变 U6(110)、U3(011)、U5(100), 需配合零电压向量 U7(111)。这样通过在不同区间内安排不同的开关切换顺序, 就可以获得对称的输出波形,其它各扇区的开关切换顺序如下表所示:
现的先后顺序为 U0、U4、U6、U7、U6、U4、U0,各电压向量的三相波形则与上表中的开关表示符号相对应。再下一个 TS 时段,Uref 的角度增加一个γ,利用式上式可以重新计算新的 T0、T4、T6 及 T7 值;这样每一个载波周期 Ts 就会合成一个新的矢量,随着θ的逐渐增大,U r e f U_ref U r e f
U r e f U_ref U r e f 空间矢量调制的第一步是判断由 Uα和 Uβ所决定的空间电压矢量所处的扇区。假定合成的电压矢量落在第 I 扇区,可知其等价条件如下:0º < arctan(Uβ/Uα) < 60 º 以上等价条件再结合矢量图几何关系分析,可以判断出合成电压矢量U r e f U_ref U r e f
若进一步分析以上的条件,有可看出参考电压矢量U r e f U_ref U r e f U β , 3 U α − U β , − 3 U α − U β U_{\beta }, \sqrt{3}U_{\alpha } - U_{\beta }, -\sqrt{3}U_{\alpha } - U_{\beta } U β , 3 U α − U β , − 3 U α − U β
U 1 = U β U 2 = 3 U α − U β U 3 = − 3 U α − U β \begin{aligned}
&U_1 = U_{\beta} \\
&U_2 = \sqrt{3}U_{\alpha } - U_{\beta } \\
&U_3 = -\sqrt{3}U_{\alpha } - U_{\beta }
\end{aligned}
U 1 = U β U 2 = 3 U α − U β U 3 = − 3 U α − U β
再定义,若 U1>0 ,则 A=1,否则 A=0; 若 U 2>0 ,则 B=1,否则 B=0;若 U3>0 ,则 C=1,否则 C=0。可以看出 A,B,C 之间共有八种组合,但由判断扇区的公式可知 A,B,C 不会同时为 1 或同时为 0,所以实际的组合是六种,A,B,C 组合取不同的值对 应着不同的扇区,并且是一一对应的,因此完全可以由 A,B,C 的组合判断所在的扇区。为区别六种状态,令 N=4 * C + 2 * B + A,则可以通过下表计算参考电压 矢量 Uref 所在的扇区。
采用上述方法,只需经过简单的加减及逻辑运算即可确定所在的扇区,对于提高系统的响应速度和进行仿真都是很有意义的。
在传统 SVPWM 算法中用到了空间角度及三角函数,使得直接计算基本电压矢量作用时间变得十分困难。实际上只要充分利用 Uα 和 Uβ 就可以使计算大为简化。以 Uref 处在第Ⅰ扇区时进行分析有:
[ U α U β ] = U r e f [ c o s ( θ ) s i n ( θ ) ] T s = 2 3 U d c ( [ 1 0 ] T 4 + [ c o s ( π 3 ) s i n ( π 3 ) ] T 6 ) \begin{bmatrix}U_{\alpha }\\ U_{\beta }\end{bmatrix} = U_{ref}\begin{bmatrix}cos(\theta )\\ sin(\theta )\end{bmatrix} T_s = \frac{2}{3}U_{dc}\left ( \begin{bmatrix}1\\ 0\end{bmatrix} T_4 + \begin{bmatrix}cos(\frac{\pi }{3})\\ sin(\frac{\pi }{3})\end{bmatrix}
T_6\right )
[ U α U β ] = U r e f [ c o s ( θ ) s i n ( θ ) ] T s = 3 2 U d c ( [ 1 0 ] T 4 + [ c o s ( 3 π ) s i n ( 3 π ) ] T 6 )
经过整理后得出:
U α T s = 2 3 U d c ( T 4 + 1 2 T 6 ) U β T s = 2 3 U d c ( 3 2 T 6 ) \begin{aligned}
&U_{\alpha } T_s = \frac{2}{3}U_{dc}(T_4 + \frac{1}{2}T_6) \\
&U_{\beta } T_s = \frac{2}{3}U_{dc}(\frac{\sqrt{3}}{2}T_6)
\end{aligned}
U α T s = 3 2 U d c ( T 4 + 2 1 T 6 ) U β T s = 3 2 U d c ( 2 3 T 6 )
T 4 = 2 U α T 2 U d c − 1 2 T 6 = 2 U α T s 2 U d c − 3 2 U β T s U d c = 3 T s U d c U 2 T 6 = 3 U β T s U d c = 3 T s U d c U 1 T 7 = T 0 = T s − T 4 − T 6 2 \begin{aligned}
&T_4 = \frac{2U_{\alpha } T}{2U_{dc}} - \frac{1}{2}T_6 = \frac{2U_{\alpha } T_s}{2U_{dc}} - \frac{\sqrt{3}}{2}\frac{U_{\beta }T_s}{U_{dc}} = \frac{\sqrt{3}T_s}{U_{dc}}U_2 \\
&T_6 = \frac{\sqrt{3} U_{\beta }T_s}{U_{dc}} = \frac{\sqrt{3}T_s}{U_{dc}}U_1 \\
&T_7 = T_0 = \frac{T_s - T_4 - T_6}{2}
\end{aligned}
T 4 = 2 U d c 2 U α T − 2 1 T 6 = 2 U d c 2 U α T s − 2 3 U d c U β T s = U d c 3 T s U 2 T 6 = U d c 3 U β T s = U d c 3 T s U 1 T 7 = T 0 = 2 T s − T 4 − T 6
同理可求得U r e f U_ref U r e f
将 I 扇区的时间图画出来如下:
SVPWM 实质是一种对在三相正弦波中注入了零序分量的调制波进行规则采样的一种变形 SPWM。但 SVPWM 的调制过程是在空间中实现的,而 SPWM 是在 ABC 坐标系下分相实现的;SPWM 的相电压调制波是正弦波,而 SVPWM 没有明确的相电压调制波,是隐含的。为了揭示 SVPWM 与 SPWM 的内在联系,需求出 SVPWM 在 ABC 坐标系上的等效调制波方程,也就是将 SVPWM 的隐含调制波显化。
[ T k t k + 1 ] = [ s i n ( k π 3 ) − c o s ( k π 3 ) s i n ( ( k − 1 ) π 3 ) − c o s ( ( k − 1 ) π 3 ) ] [ c o s ( θ ) s i n ( θ ) ] \begin{bmatrix}T_k\\ t_{k+1}\end{bmatrix} = \begin{bmatrix}
sin(\frac{k\pi }{3}) & -cos(\frac{k\pi }{3})\\
sin(\frac{(k -1) \pi }{3}) & -cos(\frac{(k-1)\pi }{3})
\end{bmatrix}\begin{bmatrix}
cos(\theta )\\
sin(\theta )
\end{bmatrix}
[ T k t k + 1 ] = [ s i n ( 3 k π ) s i n ( 3 ( k − 1 ) π ) − c o s ( 3 k π ) − c o s ( 3 ( k − 1 ) π ) ] [ c o s ( θ ) s i n ( θ ) ]
式中 m 仍为 SVPWM 调制系数,利用以上各式就可得到在第Ⅰ扇区的各相电压平均值:
U a ( θ ) = U d c T s ( − T 0 2 + T 4 2 + T 6 2 + T 7 2 + T 7 2 + T 6 2 + T 4 2 − T 0 2 ) = 3 2 ∣ U r e f ∣ c o s ( θ − π 6 ) U b ( θ ) = U d c T s ( − T 0 2 + T 4 2 + T 6 2 + T 7 2 + T 7 2 + T 6 2 + T 4 2 − T 0 2 ) = 3 2 ∣ U r e f ∣ s i n ( θ − π 6 ) U c ( θ ) = U d c T s ( − T 0 2 + T 4 2 + T 6 2 + T 7 2 + T 7 2 + T 6 2 + T 4 2 − T 0 2 ) = − 3 2 ∣ U r e f ∣ c o s ( θ − π 6 ) \begin{aligned}
&U_a(\theta ) = \frac{U_{dc}}{T_s}(-\frac{T_0}{2} + \frac{T_4}{2} + \frac{T_6}{2} + \frac{T_7}{2} + \frac{T_7}{2} + \frac{T_6}{2} + \frac{T_4}{2} - \frac{T_0}{2} ) = \frac{\sqrt{3}}{2}\left | U_{ref} \right | cos(\theta - \frac{\pi }{6}) \\
&U_b(\theta ) = \frac{U_{dc}}{T_s}(-\frac{T_0}{2} + \frac{T_4}{2} + \frac{T_6}{2} + \frac{T_7}{2} + \frac{T_7}{2} + \frac{T_6}{2} + \frac{T_4}{2} - \frac{T_0}{2} ) = \frac{\sqrt{3}}{2}\left | U_{ref} \right | sin(\theta - \frac{\pi }{6}) \\
&U_c(\theta ) = \frac{U_{dc}}{T_s}(-\frac{T_0}{2} + \frac{T_4}{2} + \frac{T_6}{2} + \frac{T_7}{2} + \frac{T_7}{2} + \frac{T_6}{2} + \frac{T_4}{2} - \frac{T_0}{2} ) = -\frac{\sqrt{3}}{2}\left | U_{ref} \right | cos(\theta - \frac{\pi }{6})
\end{aligned}
U a ( θ ) = T s U d c ( − 2 T 0 + 2 T 4 + 2 T 6 + 2 T 7 + 2 T 7 + 2 T 6 + 2 T 4 − 2 T 0 ) = 2 3 ∣ U r e f ∣ c o s ( θ − 6 π ) U b ( θ ) = T s U d c ( − 2 T 0 + 2 T 4 + 2 T 6 + 2 T 7 + 2 T 7 + 2 T 6 + 2 T 4 − 2 T 0 ) = 2 3 ∣ U r e f ∣ s i n ( θ − 6 π ) U c ( θ ) = T s U d c ( − 2 T 0 + 2 T 4 + 2 T 6 + 2 T 7 + 2 T 7 + 2 T 6 + 2 T 4 − 2 T 0 ) = − 2 3 ∣ U r e f ∣ c o s ( θ − 6 π )
同样可以推导出其它扇区的调制波函数,其相电压调制函数如下:
U a ( θ ) = { 3 2 ∣ U r e f ∣ c o s ( θ − π 6 ) − − − ( 0 ⩽ θ < π 3 , π ⩽ θ < 4 π 3 ) 3 2 ∣ U r e f ∣ c o s ( θ ) − − − ( π 3 ⩽ θ < 2 π 3 , 4 π 3 ⩽ θ < 5 π 3 ) 3 2 ∣ U r e f ∣ c o s ( θ + π 6 ) − − − ( 2 π 3 ⩽ θ < π , 5 π 3 ⩽ θ < 2 π ) U b ( θ ) = U a ( θ − 2 π 3 ) U c ( θ ) = U a ( θ − 4 π 3 ) U_a(\theta ) = \left\{\begin{matrix}
\frac{\sqrt{3}}{2}\left | U_{ref} \right | cos(\theta - \frac{\pi }{6}) ---(0 \leqslant \theta < \frac{\pi }{3}, \pi \leqslant \theta < \frac{4\pi }{3})\\
\frac{\sqrt{3}}{2}\left | U_{ref} \right | cos(\theta ) ---(\frac{\pi }{3}\leqslant \theta < \frac{2\pi }{3}, \frac{4\pi }{3} \leqslant \theta < \frac{5\pi }{3})\\
\frac{\sqrt{3}}{2}\left | U_{ref} \right | cos(\theta + \frac{\pi }{6}) ---(\frac{2\pi }{3} \leqslant \theta < \pi , \frac{5\pi }{3} \leqslant \theta < 2\pi )
\end{matrix}\right. \\
U_b(\theta ) = U_a(\theta - \frac{2\pi }{3}) \\
U_c(\theta ) = U_a(\theta - \frac{4\pi }{3})
U a ( θ ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 2 3 ∣ U r e f ∣ c o s ( θ − 6 π ) − − − ( 0 ⩽ θ < 3 π , π ⩽ θ < 3 4 π ) 2 3 ∣ U r e f ∣ c o s ( θ ) − − − ( 3 π ⩽ θ < 3 2 π , 3 4 π ⩽ θ < 3 5 π ) 2 3 ∣ U r e f ∣ c o s ( θ + 6 π ) − − − ( 3 2 π ⩽ θ < π , 3 5 π ⩽ θ < 2 π ) U b ( θ ) = U a ( θ − 3 2 π ) U c ( θ ) = U a ( θ − 3 4 π )
其线电压的调制波函数为:
U a b ( θ ) = U a ( θ ) − U b ( θ ) = 3 ∣ U r e f ∣ s i n ( θ + π 3 ) U b c ( θ ) = U a b ( θ − 2 π 3 ) U c a ( θ ) = U a ( θ − 4 π 3 ) \begin{aligned}
&U_{ab}(\theta) = U_a(\theta) - U_b(\theta) = \sqrt{3 } \left| U_{ref} \right |sin(\theta + \frac{\pi }{3}) \\
&U_{bc}(\theta ) = U_{ab}(\theta - \frac{2\pi }{3}) \\
&U_{ca}(\theta ) = U_{a}(\theta - \frac{4\pi }{3})
\end{aligned}
U a b ( θ ) = U a ( θ ) − U b ( θ ) = 3 ∣ U r e f ∣ s i n ( θ + 3 π ) U b c ( θ ) = U a b ( θ − 3 2 π ) U c a ( θ ) = U a ( θ − 3 4 π )
从相电压调制波函数来看,输出的是不规则的分段函数,为马鞍波形。当调制波为正弦波时为 spwm,调制波为在理想正弦波基础上加入三次谐波注入就是 svpwm。比单纯正弦调制波输出的 SPWM,SVPWM 的优点:
谐波优化程度高,转矩脉动小
通过共模分量注入,等效基波增大,电压利用率提高
对于一个完整当 FOC 控制器是需要电流采样的,只有在有电流采样的情况下才可以进行 clark 变换,而在实际的使用过程中有时我们并不需要进行电流闭环控制,可以采用开环控制算法,那么在没有电流反馈的情况下该如何进行开环控制呢?这里可以将 clark 变换和 park 变换省略掉,直接对 dq 轴变量进行调控,然后直接进行反 park 变换回去,再经过 svpwm 模块输出最终的信号给到电机。这里的开环控制跟有感还是无感是没有关系的,这里让然可以采用有感的开环控制,只是这里就没有办法做电流闭环控制,只能做力矩,速度和位置闭环控制。
回到一开始的 FOC 控制总体框图,整个 FOC 流程是通过电流采样获得三相电流值,对三相电流值进行 clark 变换到α β \alpha \beta α β
二相导通星形三相六状态无刷直流永磁电动机工作原理 Clark 变换与 Park 变换 如何深入理解 SVPWM? 三相对称电流通过向 dq 坐标轴上投影得到的 Id、Iq 与通过 park 变换得到的 Id、Iq 有什么区别和联系么? 深入浅出讲解 FOC 算法与 SVPWM 技术 永磁同步电机 (PMSM) 的 FOC 闭环控制详解 克拉克 (Clark) 变换中等幅值 (2/3) 和等功率 (sqrt(2/3)) 变换的公式推导 SVPWM 技术








)


