MTPA
为什么要用 MTPA
当电机采用 id=0 的控制策略,这种控制方法忽略了磁阻转矩的作用,电磁转钜方程如下:
τe=23p[ke⋅iq+(Ld−Lq)⋅id⋅iq]
转矩分为永磁转矩 Tr 和磁阻转矩 Tm,而 id=0 只剩下 Tr。这会导致电流的利用率不高,系统的效率降低。所以 id=0 的控制比较适用于隐极式电机(Ld=Lq),而对于凸极式电机并不最优,所以需要重新考虑控制策略。
推导过程
电动机电压方程:
Ud=rId−LqIqωeUq=rIq+kEωe+LdIdωe
那么电动机消耗对有功功率为:
P=23(UdId+UqIq)
将电动机方程代入功率方程得:
P=23r(Id2+Iq2)+[kEIq+(Ld−Lq)IdIq]ωe
电动机的有功功率一部分消耗在绕阻电阻上发热,另一部分用于输出机械功率:

电动机的机械功率为:
Pmech=τeωmech
机械转速与电频率之间的关系为:
ωe=pωmech
所以:
τeωmech=23r(Id2+Iq2)+[kEIq+(Ld−Lq)IdIq]pωmech
得到电磁转钜公式:
τe=23p[ke⋅iq+(Ld−Lq)⋅id⋅iq]
如果绕阻中电流峰值是 I_s
Is2=Id2+Iq2
当输出电磁转钜一定时:
Iq=23p[(kE)+(Ld−Lq)Id]τe
联立上两式得:
Is2=Id2+(23p[(kE)+(Ld−Lq)Id]τe)2
上式可以看作是一个关于Id的函数,上式有最小值,当电磁转钜一定时,有一个最小峰值电流Is,取Is最小时有:
∂Id∂Is2=2Id+2Iq23pτe[kE+(Ld−Lq)Id]2−(Ld−Lq)=2Id+2Iq23p[kE+(Ld−Lq)Id]τe[kE+(Ld−Lq)Id]−(Ld−Lq)=2Id+2Iq2[kE+(Ld−Lq)Id]−(Ld−Lq)=0
整理得:
(Ld−Lq)Id2+kEId−(Ld−Lq)Iq2=0
求解Id得到:
Id=−2(Ld−Lq)kE±(2(Ld−Lq)kE)2+Iq2
如果Ld<Lq时当电磁转钜一定时电流峰值Is最小:
Id=−2(Ld−Lq)kE−(2(Ld−Lq)kE)2+Iq2
弱磁控制
简介
弱磁控制的这个思想源还是来自他励直流电动机的调磁控制。当他励直流电动机端电压达到最大电压时,只能通过调节电机的励磁电流,进而改变励磁磁通,在保证输出电压最大值不变的条件下,使电机能恒功率运行于更高的转速。也就是说,他励直流电动机可以通过降低励磁电流达到弱磁扩速的目的。对于 PMSM 而言,励磁磁动势因永磁体产生而无法调节,只能通过调节定子电流,即增加定子直轴去磁电流分量来维持高速运行时电压的平衡。达到弱磁扩速的目的。
推导
很多应用需要马达工作在高于额定速度的范围内,这里就需要弱磁控制来实现,电流的电压约束条件如下:
(LqIq)2+(kE+LdId)2⩽ωe2U1−limit2
电流幅值约束条件:
Id2+Iq2⩽Is−limit2
MTPA 下有Id:
MTPA:Id=⎩⎪⎨⎪⎧−2(Ld−Lq)kE+sign(Ld−Lq)(2(Ld−Lq)kE)2+Iq2,Ld=Lq0,Ld=Lq
其中:
sign(x)=⎩⎪⎨⎪⎧1,x>00,x=0−1,x<0
弱磁情况下有Id:
Id=⎩⎪⎨⎪⎧−LdkE+Ld(ωeU1−limit)2−(LqIq)2,ωeU1−limit≥LqIqn/a,ωeU1−limit<LqIq
电流前馈
前馈理论
前馈控制是按照扰动量进行补偿都开环控制,当系统出现扰动时,按照扰动量当大小直接产生矫正作用。
前馈控制结构图如下:
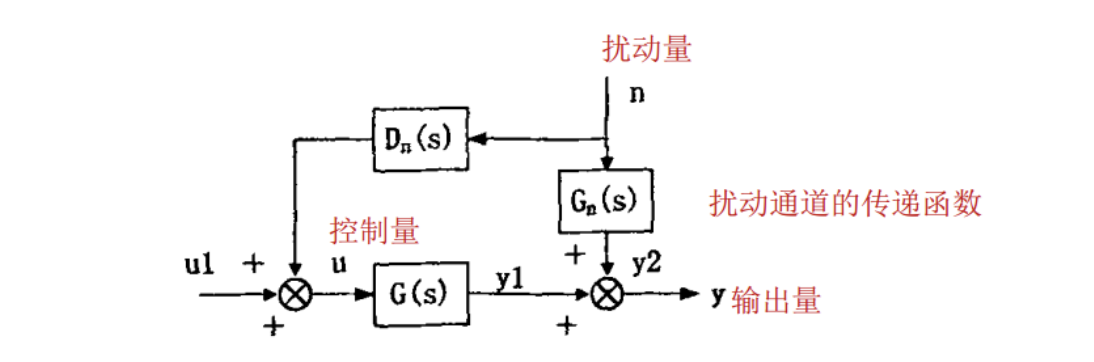
图中Gn(s)是被控对象扰动通道的传递函数,Dn(s)是前馈控制器的传递函数,G(s)为被控对象控制通道传递函数,n、u、y 分别为扰动量、控制量和输出量
假定输入量 u1=0,则有:
Y(s)=Y1(s)+Y2(s)=[Dn(s)G(s)+Gn(s)]N(s)
若使前馈控制作用完全补偿扰动作用,则应使Y(s)=0即:
Dn(s)G(s)+Gn(s)=0
所以前馈控制器的传递函数为:
Dn(s)=−G(s)Gn(s)
在实际应用中。因为前馈控制为一个开环系统。因此常常采用反馈+前馈的复合控制方式。
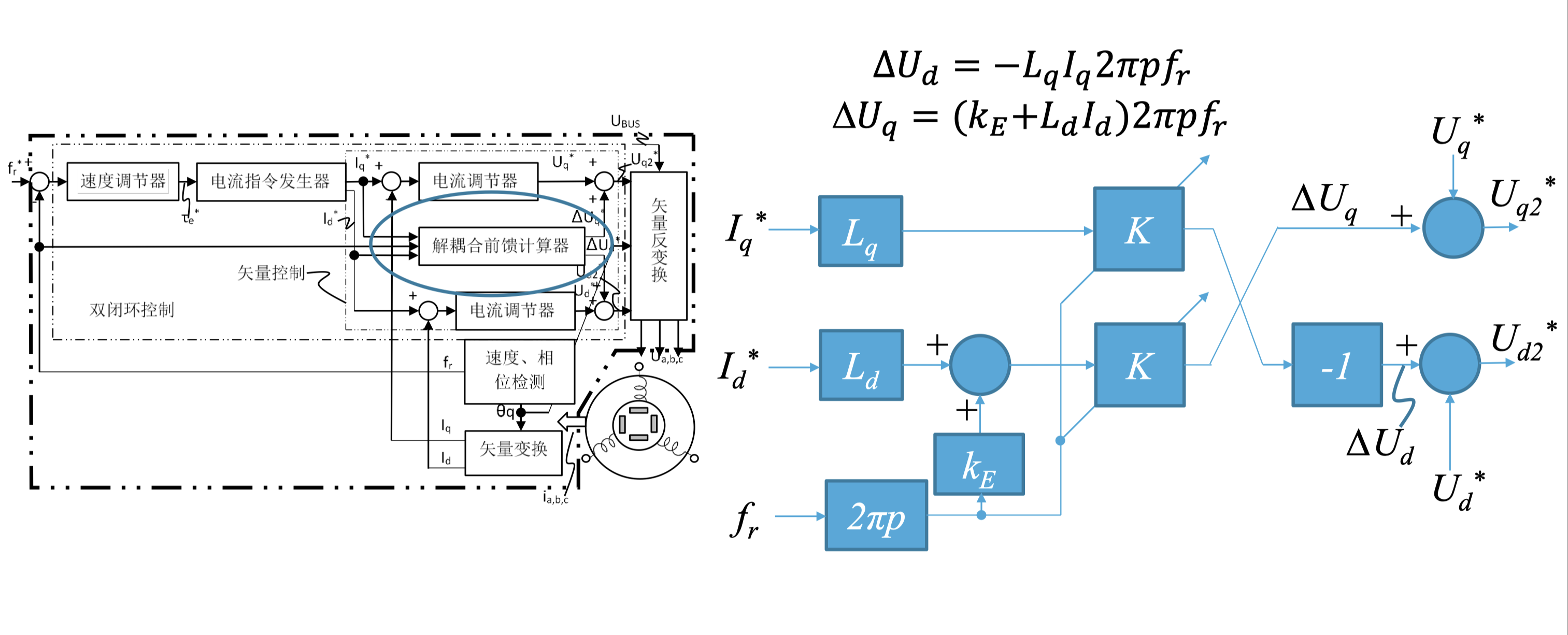
电机控制中的前馈控制
在电机控制中加入前馈控制,其结构框图如下:
参考文献
《2.ST MC SDK 5.x 矢量控制理论基础》
永磁同步电机也能弱磁调速
永磁同步电机弱磁控制
永磁同步电机-弱磁
[[focPrinciple]]
[[FOCCurrentSampling]]






)


