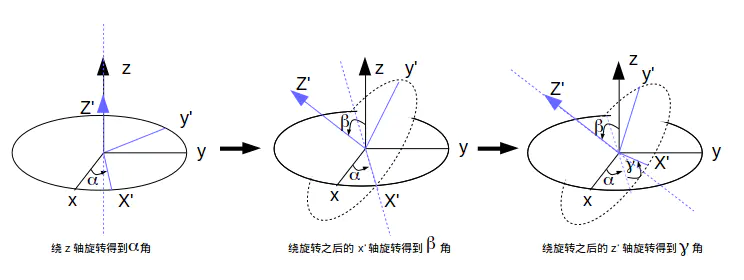
通过三角函数可以将加速度计三个轴的角速度解算为姿态角,其中 α \alpha α β \beta β γ \gamma γ γ \gamma γ
β = a r c s i n ( a x g ) γ = a r c s i n ( a y g ) \begin{aligned}
&\beta = arcsin(\frac{a_x}{g}) \\
&\gamma = arcsin(\frac{a_y}{g})
\end{aligned}
β = a r c s i n ( g a x ) γ = a r c s i n ( g a y )
其中重力加速度 $ g $ 的取值使用三轴角速度的矢量和即:
g = a x 2 + a y 2 + a z 2 g = \sqrt{a_x^{2} + a_y^{2} + a_z^{2}}
g = a x 2 + a y 2 + a z 2
将 g 的值带入上式可以得到:
β = a r c t a n ( a x a y 2 + a z 2 ) γ = a r c t a n ( a y a x 2 + a z 2 ) \begin{aligned}
&\beta = arctan(\frac{a_x}{\sqrt{a_y^{2} + a_z^{2}}}) \\
&\gamma = arctan(\frac{a_y}{\sqrt{a_x^{2} + a_z^{2}}})
\end{aligned}
β = a r c t a n ( a y 2 + a z 2 a x ) γ = a r c t a n ( a x 2 + a z 2 a y )
其中 α 为俯仰角 pitch,β 为滚转角 roll,其中航向角 yaw 是没有办法通过加速度计来计算的。
陀螺仪积分最直接的就是将陀螺仪输出的角速度与时间相乘做累加实现对角速度的积分得到角度,数据精度较高但是漂移很严重。在积分算法上常用龙格库塔法计算积分。
角速度计和陀螺仪都可以解算得到姿态角,如下:
z 1 = x + u z 2 = x + v \begin{aligned}
&z_1 = x + u \\
&z_2 = x + v
\end{aligned}
z 1 = x + u z 2 = x + v
其中 z 1 z_1 z 1 z 2 z_2 z 2 x x x u u u v v v u u u x x x
x ^ = k 1 × z 1 + k 2 × z 2 k 1 + k 2 = 1 \begin{aligned}
&\hat{x} = k_1 \times z_1 + k_2 \times z_2 \\
&k_1 + k_2 = 1
\end{aligned}
x ^ = k 1 × z 1 + k 2 × z 2 k 1 + k 2 = 1
将 k1、k2 用一阶滤波传递函数表示:
k 1 ( s ) = 1 f s + 1 k 2 ( s ) = f s f s + 1 \begin{aligned}
&k_1(s) = \frac{1}{fs + 1} \\
&k_2(s) = \frac{fs}{fs + 1}
\end{aligned}
k 1 ( s ) = f s + 1 1 k 2 ( s ) = f s + 1 f s
其中 s 是拉普拉斯变换的 s 域即频域,1 f \frac{1}{f} f 1
x ^ ( s ) = k 1 ( s ) z 1 ( s ) + k 2 ( s ) z 2 ( s ) = 1 f s + 1 z 1 ( s ) + f s f s + 1 z 2 ( s ) \hat{x}(s) = k_1(s)z_1(s) + k_2(s)z_2(s) = \frac{1}{fs+1}z_1(s) + \frac{fs}{fs+1}z_2(s)
x ^ ( s ) = k 1 ( s ) z 1 ( s ) + k 2 ( s ) z 2 ( s ) = f s + 1 1 z 1 ( s ) + f s + 1 f s z 2 ( s )
根据拉普拉斯变换微分定理变换公式:
L [ d n f ( t ) d t n ] = s n F ( s ) L[\frac{d^{n}f(t)}{dt^{n}}] = s^{n} F(s)
L [ d t n d n f ( t ) ] = s n F ( s )
用拉普拉斯反变换回去得到:
f x ^ ˙ ( t ) + x ^ ( t ) = z 1 ( t ) + f z 2 ^ ˙ ( t ) f\dot{\hat{x}}(t) + \hat{x}(t) = z_1(t) + f\dot{\hat{z_2}}(t)
f x ^ ˙ ( t ) + x ^ ( t ) = z 1 ( t ) + f z 2 ^ ˙ ( t )
离散化后得到:
f x ^ ( k ) − x ^ ( k − 1 ) d t + x ^ k = z 1 ( k ) + f z 2 ^ ( k ) − z 2 ^ ( k − 1 ) d t f\frac{\hat{x}(k) - \hat{x}(k-1)}{dt} + \hat{x}_k = z_1(k) + f\frac{\hat{z_2}(k) - \hat{z_2}(k-1)}{dt}
f d t x ^ ( k ) − x ^ ( k − 1 ) + x ^ k = z 1 ( k ) + f d t z 2 ^ ( k ) − z 2 ^ ( k − 1 )
化简整理后得:
x ^ ( k ) = f f + d t [ x ^ ( k − 1 ) + z 2 ( k ) − z 2 ( k − 1 ) ] + d t f + d t z 1 ( k ) \hat{x}(k) = \frac{f}{f+dt}[\hat{x}(k-1) + z_2(k) - z_2(k-1)] + \frac{dt}{f+dt}z_1(k)
x ^ ( k ) = f + d t f [ x ^ ( k − 1 ) + z 2 ( k ) − z 2 ( k − 1 ) ] + f + d t d t z 1 ( k )
取
K = d t f + d t K=\frac{dt}{f+dt}
K = f + d t d t
得到:
x ^ ( k ) = ( 1 − K ) [ x ^ ( k − 1 ) + z 2 ( k ) − z 2 ( k − 1 ) ] + K z 1 ( k ) \hat{x}(k) = (1-K)[\hat{x}(k-1) + z_2(k) - z_2(k-1)] + K z_1(k)
x ^ ( k ) = ( 1 − K ) [ x ^ ( k − 1 ) + z 2 ( k ) − z 2 ( k − 1 ) ] + K z 1 ( k )
这就是一阶互补滤波的最终公式。
将上面推导出的公式写成代码如下:
1 2 3 4 5 6 7 8 9 10 11 /** * @brief 一阶互补滤波器单轴 * @param acc_angle 通过三角函数计算加速度计的值得到的角度值 * @param gyro_rate 陀螺仪输出的角速度值 * @param K1 滤波器系数,远小于 1 * @return 返回融合后角度值 */ static void firstOrderComplementaryFiltering(float acc_angle, float gyro_rate, float * angle) { *angle = K * acc_angle + (1 - K) * (*angle + gyro_rate * dt); }
陀螺仪采样率是 1kHZ,dt 为 0.001 则算法涉及的参数只有一个就是 K 参数,假如取截止频率为 100 的话:
K = d t f + d t = 0.001 1 100 + 0.001 ≐ 0.1 K = \frac{dt}{f + dt} = \frac{0.001}{\frac{1}{100} + 0.001} \doteq 0.1
K = f + d t d t = 1 0 0 1 + 0 . 0 0 1 0 . 0 0 1 ≐ 0 . 1
卡尔曼滤波包括预测和更新两个过程,下面是两个过程的详细推导:
预测阶段主要是根据陀螺仪数据预测角度值,系统状态量是角度值和角速度偏差,而不是角度值和角速度值:
x ^ ( k ∣ k − 1 ) = x ^ ( k − 1 ∣ k − 1 ) + ( θ ˊ − θ ˊ b ) △ t + w θ θ ˊ b ( k ∣ k − 1 ) = θ ˊ b ( k − 1 ∣ k − 1 ) + w θ ˊ b w ( k ) = [ w θ w θ ˊ b ] \begin{aligned}
&\hat{x}(k|k-1) = \hat{x}(k-1|k-1) + (\acute{\theta} - \acute{\theta }_b) \bigtriangleup t + w_\theta \\
&\acute{\theta }_b(k|k-1) = \acute{\theta }_b(k-1|k-1) + w_{\acute{\theta }_b} \\
&w(k) = \begin{bmatrix}w_{\theta } &w_{\acute{\theta}_b}\end{bmatrix}
\end{aligned}
x ^ ( k ∣ k − 1 ) = x ^ ( k − 1 ∣ k − 1 ) + ( θ ˊ − θ ˊ b ) △ t + w θ θ ˊ b ( k ∣ k − 1 ) = θ ˊ b ( k − 1 ∣ k − 1 ) + w θ ˊ b w ( k ) = [ w θ w θ ˊ b ]
其中 θ ˊ b \acute{\theta}_b θ ˊ b θ ˊ \acute{\theta } θ ˊ w ( k ) w(k) w ( k )
x ^ ( k ∣ k − 1 ) = F x ^ ( k − 1 ∣ k − 1 ) + B θ ˊ ( k ) + W ( K ) F = [ 1 − △ t 0 1 ] B = [ △ T 0 ] (1) \hat{x}(k|k-1) = F\hat{x}(k-1|k-1) + B\acute{\theta }(k) +W(K) \tag{1} \\
F = \begin{bmatrix}1 & - \bigtriangleup t\\ 0&1 \end{bmatrix} \\
B=\begin{bmatrix}\bigtriangleup T \\ 0\end{bmatrix}
x ^ ( k ∣ k − 1 ) = F x ^ ( k − 1 ∣ k − 1 ) + B θ ˊ ( k ) + W ( K ) F = [ 1 0 − △ t 1 ] B = [ △ T 0 ] ( 1 )
将矩阵写成展开形式:
[ θ k θ ˊ b ] = [ 1 − △ t 0 1 ] [ θ k − 1 θ ˊ k − 1 ] + [ △ t 0 ] θ ˊ k + w k \begin{bmatrix}\theta_k\\ \acute{\theta }_b\end{bmatrix} = \begin{bmatrix}1 & -\bigtriangleup t\\ 0&1 \end{bmatrix}\begin{bmatrix}\theta_{k-1}\\ \acute{\theta }_{k-1}\end{bmatrix} + \begin{bmatrix}\bigtriangleup t\\ 0\end{bmatrix}\acute{\theta }_k + w_k
[ θ k θ ˊ b ] = [ 1 0 − △ t 1 ] [ θ k − 1 θ ˊ k − 1 ] + [ △ t 0 ] θ ˊ k + w k
1 2 3 4 5 6 7 /* * kalman 公式一、角度的先验状态估计 x(k|k-1) = F * x(k-1|k-1) + B* u * x 为角度和角速度的列向量 F=([1,-dt], * [0, 1]) */ gyro_rate-=q_bias; *angle+=gyro_rate * dt;
协方差矩阵的更新如下:
C o v ( x ) = Σ c o v ( A x ) = A Σ A T c o v ( A x ) = E [ ( A x − E [ A x ] ) ( A x − E [ A x ] ) T ] = E [ A x − A E [ x ] ( A x − A E [ x ] ) T ] = E ( A ( x − E [ x ] ) ( x − E [ x ] ) T A T ) = A E [ ( X − E [ x ] ) ( X − E [ x ] ) T ] A T = A Σ A T \begin{aligned}
&Cov(x) = \Sigma \\
&cov(Ax) = A\Sigma A^{T} \\
cov(Ax)& = E[(Ax - E[Ax])(Ax - E[Ax])^{T}] \\
&= E[Ax -AE[x](Ax - AE[x])^{T}] \\
&= E(A(x-E[x])(x-E[x])^{T}A^{T}) \\
&= AE[(X-E[x])(X-E[x])^{T}]A^{T} \\
&= A\Sigma A^{T}
\end{aligned}
c o v ( A x ) C o v ( x ) = Σ c o v ( A x ) = A Σ A T = E [ ( A x − E [ A x ] ) ( A x − E [ A x ] ) T ] = E [ A x − A E [ x ] ( A x − A E [ x ] ) T ] = E ( A ( x − E [ x ] ) ( x − E [ x ] ) T A T ) = A E [ ( X − E [ x ] ) ( X − E [ x ] ) T ] A T = A Σ A T
故协方差方程为:
P e x p e c t ( K ∣ K − 1 ) = F P ( K − 1 ∣ K − 1 ) F T + Q k (2) P_{expect}(K|K-1) = FP(K-1|K-1)F^{T} + Q_k \tag{2}
P e x p e c t ( K ∣ K − 1 ) = F P ( K − 1 ∣ K − 1 ) F T + Q k ( 2 )
这个方程表达的是新的协方差由上一次的协方差通过矩阵变换而来且再加上外部干扰,而协方差矩阵表征的是一个误差范围也就是不确定性,每次的不确定性由上一次的不确定性通过矩阵变换加上新的不确定性而来。将矩阵写为展开形式并化简得到:
[ P 00 P 01 P 10 P 11 ] k ∣ k − 1 = [ 1 − △ t 0 1 ] [ P 00 P 01 P 10 P 11 ] k − 1 ∣ k − 1 [ 1 0 − △ t 1 ] + [ Q θ 0 0 Q θ ˊ ] △ t = [ P 00 − △ t P 10 P 01 − △ t P 11 P 10 P 11 ] k − 1 ∣ k − 1 [ 1 0 − △ t 1 ] + [ Q θ 0 0 Q θ ˊ ] △ t = [ P 00 − △ t P 10 − △ t ( P 01 − △ t P 11 ) P 01 − △ t P 11 P 10 − △ t P 11 P 11 ] k − 1 ∣ k − 1 + [ Q θ 0 0 Q θ ˊ ] △ t = [ P 00 − △ t P 10 − △ t ( P 01 − △ t P 11 ) + Q θ △ t P 01 − △ t P 11 P 10 − △ t P 11 P 11 + Q θ ˊ △ t ] = [ P 00 − △ t ( △ t P 11 − P 10 − P 01 + Q θ ) P 01 − △ t P 11 P 10 − △ t P 11 P 11 + Q θ ˊ △ t ] \begin{aligned}
\begin{bmatrix}P_{00} &P_{01} \\ P_{10}& P_{11}\end{bmatrix}_{k|k-1} &= \begin{bmatrix}1 & -\bigtriangleup t\\ 0&1 \end{bmatrix}\begin{bmatrix}P_{00} &P_{01} \\ P_{10}& P_{11}\end{bmatrix}_{k-1|k-1}\begin{bmatrix}1 & 0\\ -\bigtriangleup t&1 \end{bmatrix} + \begin{bmatrix}Q_\theta & 0\\ 0&Q_{\acute{\theta }} \end{bmatrix}\bigtriangleup t \\
&=\begin{bmatrix}P_{00}-\bigtriangleup tP_{10} &P_{01}-\bigtriangleup tP_{11} \\ P_{10}&P_{11} \end{bmatrix}_{k-1|k-1}\begin{bmatrix}1 & \\ 0-\bigtriangleup t & 1\end{bmatrix} + \begin{bmatrix}Q_\theta & 0\\ 0&Q_{\acute{\theta }} \end{bmatrix}\bigtriangleup t \\
&=\begin{bmatrix}P_{00}-\bigtriangleup tP_{10}-\bigtriangleup t(P_{01}-\bigtriangleup tP_{11}) &P_{01}-\bigtriangleup tP_{11} \\ P_{10}-\bigtriangleup tP_{11}&P_{11} \end{bmatrix}_{k-1|k-1} + \begin{bmatrix}Q_\theta & 0\\ 0&Q_{\acute{\theta }} \end{bmatrix}\bigtriangleup t \\
&=\begin{bmatrix}P_{00}-\bigtriangleup tP_{10}-\bigtriangleup t(P_{01}-\bigtriangleup tP_{11}) +Q_\theta \bigtriangleup t&P_{01}-\bigtriangleup tP_{11} \\ P_{10}-\bigtriangleup tP_{11}&P_{11}+Q_{\acute{\theta }}\bigtriangleup t \end{bmatrix} \\
&=\begin{bmatrix}P_{00}-\bigtriangleup t(\bigtriangleup tP_{11}-P_{10}-P_{01} +Q_\theta )&P_{01}-\bigtriangleup tP_{11} \\ P_{10}-\bigtriangleup tP_{11}&P_{11}+Q_{\acute{\theta }}\bigtriangleup t \end{bmatrix}
\end{aligned}
[ P 0 0 P 1 0 P 0 1 P 1 1 ] k ∣ k − 1 = [ 1 0 − △ t 1 ] [ P 0 0 P 1 0 P 0 1 P 1 1 ] k − 1 ∣ k − 1 [ 1 − △ t 0 1 ] + [ Q θ 0 0 Q θ ˊ ] △ t = [ P 0 0 − △ t P 1 0 P 1 0 P 0 1 − △ t P 1 1 P 1 1 ] k − 1 ∣ k − 1 [ 1 0 − △ t 1 ] + [ Q θ 0 0 Q θ ˊ ] △ t = [ P 0 0 − △ t P 1 0 − △ t ( P 0 1 − △ t P 1 1 ) P 1 0 − △ t P 1 1 P 0 1 − △ t P 1 1 P 1 1 ] k − 1 ∣ k − 1 + [ Q θ 0 0 Q θ ˊ ] △ t = [ P 0 0 − △ t P 1 0 − △ t ( P 0 1 − △ t P 1 1 ) + Q θ △ t P 1 0 − △ t P 1 1 P 0 1 − △ t P 1 1 P 1 1 + Q θ ˊ △ t ] = [ P 0 0 − △ t ( △ t P 1 1 − P 1 0 − P 0 1 + Q θ ) P 1 0 − △ t P 1 1 P 0 1 − △ t P 1 1 P 1 1 + Q θ ˊ △ t ]
Q k Q_k Q k △ t \bigtriangleup t △ t
Q k = [ Q θ 0 0 Q θ ˊ b ] △ t Q_k = \begin{bmatrix}Q_\theta & 0\\ 0& Q_{\acute{\theta }_b}\end{bmatrix}\bigtriangleup t \\
Q k = [ Q θ 0 0 Q θ ˊ b ] △ t
其中 Q θ ˊ b Q_{\acute{\theta }_b} Q θ ˊ b Q θ Q_\theta Q θ
1 2 3 4 5 6 7 /* * kalman 公式二、预测协方差矩阵 P(k|k-1) = F * P(k-1|k-1) * F' + Q(k) */ P[0][0] += (Q_angle - P[0][1] - P[1][0] + P[1][1] * dt) * dt; P[0][1] += (-P[1][1]) * dt; P[1][0] += (-P[1][1]) * dt; P[1][1] += Q_gyro * dt;
观测值 z k z_k z k
z k = H ∗ x k + v k z_k = H * x_k + v_k
z k = H ∗ x k + v k
这里 z k z_k z k H H H H = [ [ 1 0 ] ] H=[\begin{bmatrix}1 &0 \end{bmatrix}] H = [ [ 1 0 ] ] H H H v k v_k v k
z k ∼ N ( 0 , R ) z_k \sim N(0,R)
z k ∼ N ( 0 , R )
本系统中测量值只有一个角速度值,因此R R R v k = v v_k = v v k = v
P m e a s u r e ( k ∣ k ) = H ∗ P ( k ∣ k − 1 ) H T + R P_{measure}(k|k) = H*P(k|k-1)H^{T} + R
P m e a s u r e ( k ∣ k ) = H ∗ P ( k ∣ k − 1 ) H T + R
将其写成矩阵展开形式并化简得到如下:
P m e a s u r e ( k ∣ k ) = [ 1 0 ] ∗ [ P 00 P 01 P 10 P 11 ] k ∣ k − 1 ∗ [ 1 0 ] + R = P 00 k ∣ k − 1 + R P_{measure}(k|k) =\begin{bmatrix}1 &0 \end{bmatrix} * \begin{bmatrix}P_{00} &P_{01} \\ P_{10} &P_{11} \end{bmatrix}_{k|k-1} *
\begin{bmatrix}1\\ 0\end{bmatrix} + R
= P_{00 k|k-1} +R
P m e a s u r e ( k ∣ k ) = [ 1 0 ] ∗ [ P 0 0 P 1 0 P 0 1 P 1 1 ] k ∣ k − 1 ∗ [ 1 0 ] + R = P 0 0 k ∣ k − 1 + R
1 2 3 4 5 6 /* * 中间变量 E = H * P(k|k-1) H' + R */ PCt_0 = C_0 * P[0][0]; PCt_1 = C_0 * P[1][0]; E = R_angle + C_0 * PCt_0;
测量过程的协方差结果就是一个数值(看到这应该很庆幸不用对矩阵进行求逆,这个参数其实就是卡尔曼增益里面求逆矩阵那一项),其实就是方差值。到这里有两个协方差,一个是预测过程的协方差另一个是测量过程的协方差,两个协方差代表了两个数据源的噪声,哪个值大代表哪个过程的噪声越大,对其信任度就会降低。
K = H k ∗ P k ∗ H k T ( H k ∗ P k ∗ H k T + R ) − 1 K = H_k*P_k*H^{T}_k (H_k*P_k*H^{T}_k + R)^{-1}
K = H k ∗ P k ∗ H k T ( H k ∗ P k ∗ H k T + R ) − 1
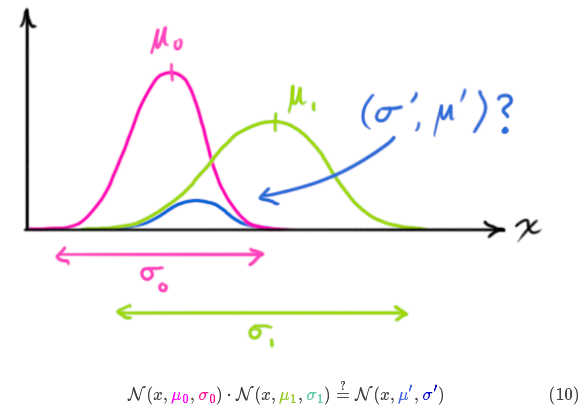
这个公式看起来非常不友好,其实卡尔曼系数是将上面通过预测和测量得到的两个高斯方程相乘而得到的。具体可以参考以下链接,其中之一是中文翻译版:How a Kalman filter works, in pictures 详解卡尔曼滤波原理
这张图是原作者的图但是有些不准确,蓝色的融合后的曲线应该是更高的曲线才对。将红色和绿色两个高斯方程相乘可以得到蓝色曲线代表的高斯方程,这就是估计的最优值。先看一维数据下的高斯方程相乘的结果如下:
μ ′ = μ 0 + σ 0 2 ( μ 1 − μ 0 ) σ 0 2 + σ 1 2 σ ′ 2 = σ 0 2 − σ 0 4 σ 0 2 + σ 1 2 \begin{aligned}
&{\mu }' = \mu_0 + \frac{\sigma_0 ^{2} (\mu_1 - \mu_0)}{\sigma_0 ^{2} + \sigma_1 ^{2}} \\
&{\sigma}'^{2} = \sigma_0^{2} - \frac{\sigma_0^{4}}{\sigma_0 ^{2} + \sigma_1 ^{2}}
\end{aligned}
μ ′ = μ 0 + σ 0 2 + σ 1 2 σ 0 2 ( μ 1 − μ 0 ) σ ′ 2 = σ 0 2 − σ 0 2 + σ 1 2 σ 0 4
取
k = σ 0 2 σ 0 2 + σ 1 2 k = \frac{\sigma_0^{2}}{\sigma_0 ^{2} + \sigma_1 ^{2}}
k = σ 0 2 + σ 1 2 σ 0 2
得到:
μ ′ = μ 0 + k ( μ 1 − μ 0 ) σ ′ 2 = σ 0 2 − k σ 0 2 \begin{aligned}
&{\mu }' = \mu_0 + k(\mu_1 - \mu_0) \\
&{\sigma}'^{2} = \sigma_0 ^{2} - k \sigma_0 ^{2}
\end{aligned}
μ ′ = μ 0 + k ( μ 1 − μ 0 ) σ ′ 2 = σ 0 2 − k σ 0 2
用 Σ \Sigma Σ
K = Σ 0 ( Σ 0 + Σ 1 ) − 1 μ ′ ⃗ = μ 0 ⃗ + K ( μ 1 ⃗ − μ 0 ⃗ ) Σ ′ = Σ 0 − K Σ 0 \begin{aligned}
&K = \Sigma_0 (\Sigma_0 + \Sigma_1)^{-1} \\
&\vec{\mu'} = \vec{\mu_0} + K (\vec{\mu_1} - \vec{\mu_0}) \\
&{\Sigma}' = \Sigma_0 - K \Sigma_0
\end{aligned}
K = Σ 0 ( Σ 0 + Σ 1 ) − 1 μ ′ = μ 0 + K ( μ 1 − μ 0 ) Σ ′ = Σ 0 − K Σ 0
将我们前面推导的预测和测量带入到上面的公式就得到下面卡尔曼滤波的后三个公式如下:
K = H k ∗ P k ∗ H k T ( H k ∗ P k ∗ H k T + R ) − 1 H k ∗ x ^ k ∣ k = H k ∗ x ^ k ∣ k − 1 + K ( z k − H k ∗ x ^ k ∣ k − 1 ) H k ∗ P k ∣ k ′ ∗ H k T = H k ∗ P k ∣ k ∗ H k T − K ∗ ( H k ∗ P k ∣ k ∗ H k T ) \begin{aligned}
&K = H_k * P_k * H^{T}_k (H_k * P_k * H^{T}_k + R)^{-1} \\
&H_k * \hat{x}_{k|k} = H_k * \hat{x}_{k|k-1} + K (z_k - H_k * \hat{x}_{k|k-1}) \\
&H_k * {P}'_{k|k} * H^{T}_k = H_k * P_{k|k} * H^{T}_k - K * (H_k * P_{k|k} * H^{T}_k)
\end{aligned}
K = H k ∗ P k ∗ H k T ( H k ∗ P k ∗ H k T + R ) − 1 H k ∗ x ^ k ∣ k = H k ∗ x ^ k ∣ k − 1 + K ( z k − H k ∗ x ^ k ∣ k − 1 ) H k ∗ P k ∣ k ′ ∗ H k T = H k ∗ P k ∣ k ∗ H k T − K ∗ ( H k ∗ P k ∣ k ∗ H k T )
将这三个方程联系起来做运算得到如下更新方程:
K k = P k ∣ k − 1 ∗ H T ∗ P m e a s u r e − 1 ( k ∣ k ) (3) K_k = P_{k|k-1} * H^T * P^{-1}_{measure}(k|k) \tag{3}
K k = P k ∣ k − 1 ∗ H T ∗ P m e a s u r e − 1 ( k ∣ k ) ( 3 )
将其写为矩阵展开形式并化简得到:
[ K 0 K 1 ] k = [ P 00 P 01 P 10 P 11 ] k ∣ k − 1 ∗ [ 1 0 ] ∗ P m e a s u r e − 1 ( k ∣ k ) = [ P 00 P 10 ] k ∣ k − 1 ∗ P m e a s u r e − 1 ( k ∣ k ) \begin{aligned}
\begin{bmatrix}K_0\\ K_1\end{bmatrix}_k &= \begin{bmatrix}P_{00} &P_{01} \\ P_{10}&P_{11} \end{bmatrix}_{k|k-1} * \begin{bmatrix}1\\ 0\end{bmatrix} * P^{-1}_{measure}(k|k) \\
&=\begin{bmatrix}P_{00}\\ P_{10}\end{bmatrix}_{k|k-1} * P^{-1}_{measure}(k|k)
\end{aligned}
[ K 0 K 1 ] k = [ P 0 0 P 1 0 P 0 1 P 1 1 ] k ∣ k − 1 ∗ [ 1 0 ] ∗ P m e a s u r e − 1 ( k ∣ k ) = [ P 0 0 P 1 0 ] k ∣ k − 1 ∗ P m e a s u r e − 1 ( k ∣ k )
1 2 3 4 5 /* * kalman 公式三、K = P(k|k-1) * H' / (H * P(k|k-1) H' + R) */ K_0 = PCt_0 / E; K_1 = PCt_1 / E;
协方差的更新:
P k ∣ k = ( I − K k ∗ H k ) P k ∣ k − 1 (4) P_{k|k} = (I - K_k* H_k)P_{k|k-1} \tag{4}
P k ∣ k = ( I − K k ∗ H k ) P k ∣ k − 1 ( 4 )
将矩阵写为展开形式并化简得到如下:
[ P 00 P 01 P 10 P 11 ] k = ( [ 1 0 0 1 ] − [ K 0 K 1 ] k ∗ [ 1 0 ] ) ∗ [ P 00 P 01 P 10 P 11 ] k − 1 = ( [ 1 0 0 1 ] − [ K 0 0 K 1 0 ] k ) ∗ [ P 00 P 01 P 10 P 11 ] k − 1 = [ P 00 P 01 P 10 P 11 ] k − 1 − [ K 0 P 00 K 0 P 01 K 1 P 00 K 1 P 01 ] \begin{aligned}
\begin{bmatrix}P_{00} & P_{01} \\ P_{10} & P_{11}\end{bmatrix}_k &= (\begin{bmatrix}1 & 0\\ 0 & 1\end{bmatrix} -\begin{bmatrix}K_0\\ K_1\end{bmatrix}_k * \begin{bmatrix}1 & 0 \end{bmatrix}) * \begin{bmatrix}P_{00} & P_{01} \\ P_{10} & P_{11}\end{bmatrix}_{k-1} \\
&=(\begin{bmatrix}1 & 0\\ 0 & 1\end{bmatrix} -\begin{bmatrix}K_0 &0 \\ K_1 &0 \end{bmatrix}_k) * \begin{bmatrix}P_{00} & P_{01} \\ P_{10} & P_{11}\end{bmatrix}_{k-1} \\
&=\begin{bmatrix}P_{00} & P_{01} \\ P_{10} & P_{11}\end{bmatrix}_{k-1} - \begin{bmatrix}K_0P_{00} &K_0P_{01} \\ K_1P_{00} &K_1P_{01} \end{bmatrix}
\end{aligned}
[ P 0 0 P 1 0 P 0 1 P 1 1 ] k = ( [ 1 0 0 1 ] − [ K 0 K 1 ] k ∗ [ 1 0 ] ) ∗ [ P 0 0 P 1 0 P 0 1 P 1 1 ] k − 1 = ( [ 1 0 0 1 ] − [ K 0 K 1 0 0 ] k ) ∗ [ P 0 0 P 1 0 P 0 1 P 1 1 ] k − 1 = [ P 0 0 P 1 0 P 0 1 P 1 1 ] k − 1 − [ K 0 P 0 0 K 1 P 0 0 K 0 P 0 1 K 1 P 0 1 ]
1 2 3 4 5 6 7 8 9 /* * kalman 公式四、P(k|k) = (I - K * H) * P(k|k-1) */ t_0 = PCt_0; t_1 = C_0 * P[0][1]; P[0][0] -= K_0 * t_0; P[0][1] -= K_0 * t_1; P[1][0] -= K_1 * t_0; P[1][1] -= K_1 * t_1;
下面是最优估计值
x ^ k ∣ k = x ^ k ∣ k − 1 + K ∗ ( z k − H k ∗ x ^ k ∣ k − 1 ) (5) \hat{x}_{k|k} = \hat{x}_{k|k-1} + K * (z_k - H_k * \hat{x}_{k|k-1}) \tag{5}
x ^ k ∣ k = x ^ k ∣ k − 1 + K ∗ ( z k − H k ∗ x ^ k ∣ k − 1 ) ( 5 )
写成矩阵的展开形式并化简如下:
[ θ θ b ˊ ] k ∣ k = [ θ θ b ˊ ] k ∣ k − 1 + [ K 0 K 1 ] k ∗ ( z k − θ k ∣ k − 1 ) \begin{bmatrix}\theta \\ \acute{\theta_b}\end{bmatrix}_{k|k} = \begin{bmatrix}\theta \\ \acute{\theta_b}\end{bmatrix}_{k|k-1} + \begin{bmatrix}K_0\\ K_1\end{bmatrix}_k * (z_k - \theta_{k|k-1})
[ θ θ b ˊ ] k ∣ k = [ θ θ b ˊ ] k ∣ k − 1 + [ K 0 K 1 ] k ∗ ( z k − θ k ∣ k − 1 )
1 2 3 4 5 6 7 8 9 10 11 /* * 中间变量 角度残差 z(k) - H * x(k) * H = ([1,0]) */ angle_err = acc_angle - *angle; /* * kalman 公式五、x(k|k) = x(k|k-1) + K * (z(k) - H * x(k)) */ *angle += K_0 * angle_err; q_bias += K_1 * angle_err;
以上就是卡尔曼滤波的预测和更新过程。但是我们前面在说卡尔曼系数的时候是将两个卡尔曼方程相乘得到了最优解,这里有个问题就是这种方式得到的值是不是合理,或者说卡尔曼滤波是不是无偏估计的,这里贴出网上的一个推导,自行查看。https://www.zhihu.com/question/331568328/answer/735287556
卡尔曼系数K K K
x ^ k ∣ k = x ^ k ∣ k − 1 + K ∗ ( z k − H k ∗ x ^ k ∣ k − 1 ) \hat{x}_{k|k} = \hat{x}_{k|k-1} + K * (z_k - H_k * \hat{x}_{k|k-1})
x ^ k ∣ k = x ^ k ∣ k − 1 + K ∗ ( z k − H k ∗ x ^ k ∣ k − 1 )
这个式子中 H k H_k H k K K K 0 0 0 K K K z k z_k z k K K K K K K K K K Q Q Q R R R Q Q Q Q θ Q_{\theta } Q θ Q θ ˊ Q_{\acute{\theta }} Q θ ˊ R R R 100 u g / h z 100ug/\sqrt{hz} 1 0 0 u g / h z 100 u g ∗ 1000 100ug * \sqrt{1000} 1 0 0 u g ∗ 1 0 0 0 R R R R R R R R R Q Q Q R R R
ω = ω ^ + b g + n g \omega = \hat{\omega} + b_g + n_g
ω = ω ^ + b g + n g
这里, ω \omega ω ω ^ \hat{\omega} ω ^ b g b_g b g n g n_g n g
a = R T ( a ^ − g ) + b a + n a a = R^{T}(\hat{a} - g) + b_a + n_a
a = R T ( a ^ − g ) + b a + n a
这里a a a a ^ \hat{a} a ^ R R R g g g b a b_a b a n a n_a n a
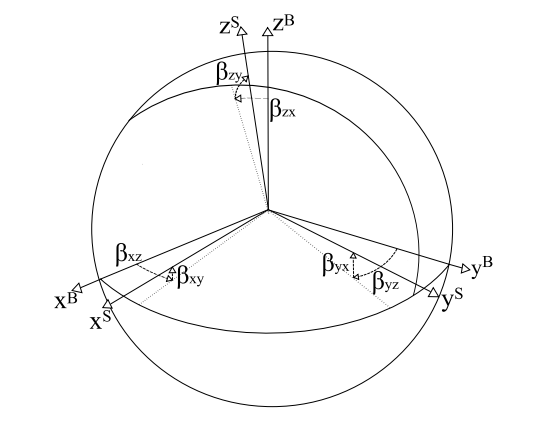
在开始讨论 mahony 滤波器公式之前,让我们正式定义将要使用的坐标轴。让 I , W , B I,W,B I , W , B B B B I I I
从传感器获取陀螺仪和 acc 测量值。让 I w t I_{w_t} I w t I a t I_{a_t} I a t I a ^ t I_{\hat{a}_t} I a ^ t
1 2 3 4 recipNorm = invSqrt(ax * ax + ay * ay + az * az); ax *= recipNorm; ay *= recipNorm; az *= recipNorm;
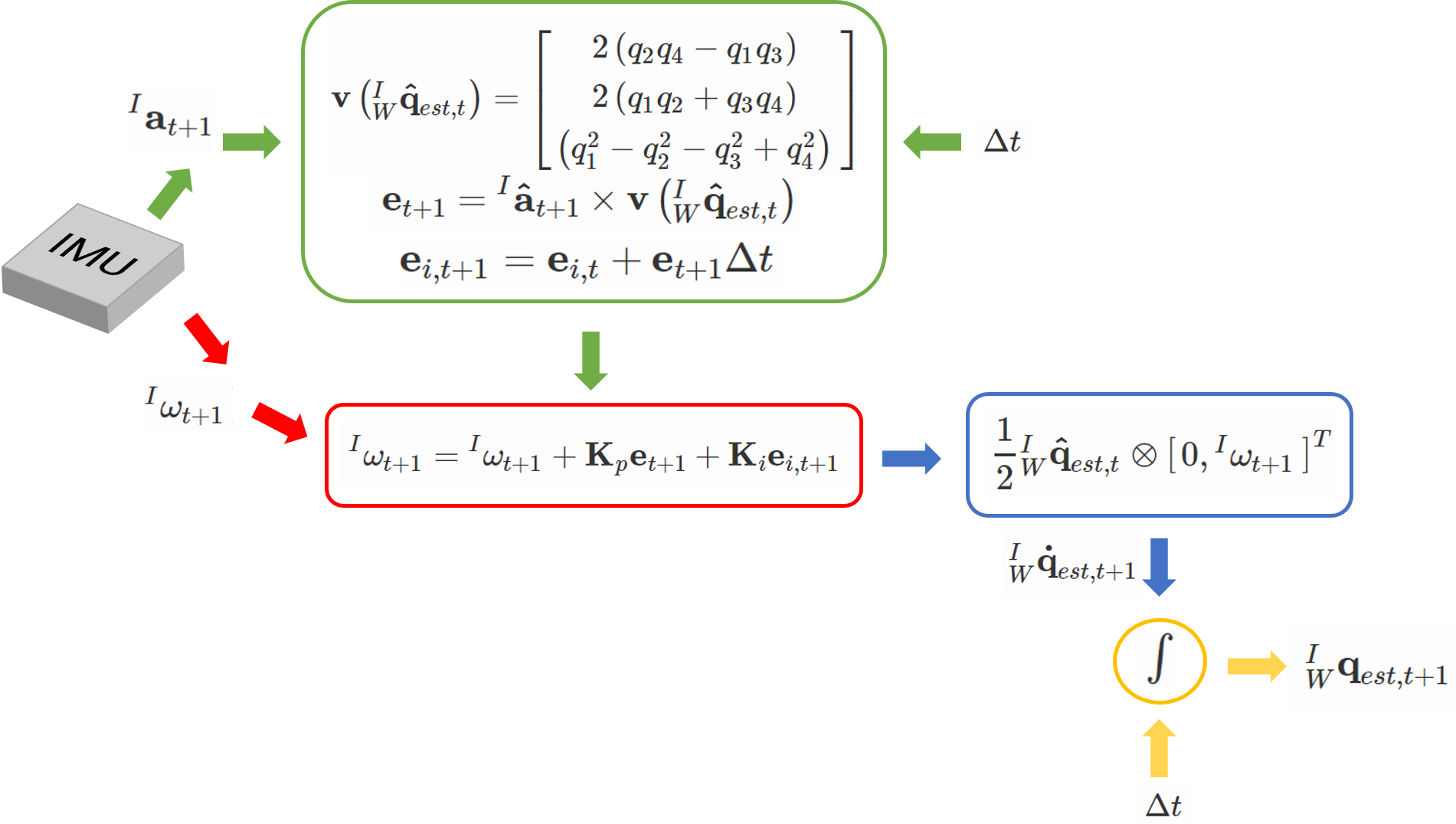
根据先验估计值利用 acc 计算误差:
v ( I W q e s t ^ , t ) = [ 2 ( q 2 q 4 − q 1 q 3 ) 2 ( q 1 q 2 + q 3 q 4 ) ( q 1 2 − q 2 2 − q 3 2 + q 4 2 ) ] e t + 1 = I a t + 1 ^ × v ( I W q e s t ^ , t ) e i , t + 1 = e i , t + e t + 1 Δ t \begin{aligned}
&v(\hat{_{I}^{W}\textrm{}q_{est}},t) = \begin{bmatrix}2(q_2q_4-q_1q_3)\\ 2(q_1q_2+q_3q_4)\\ (q_1^{2} - q_2^{2} - q_3^{2} + q_4^{2})\end{bmatrix} \\
&e_{t+1} = I_{\hat{a_{t+1}}} \times v(\hat{_{I}^{W}\textrm{}q_{est}},t) \\
&e_{i,t+1} = e_{i,t} + e_{t+1}\Delta t
\end{aligned}
v ( I W q e s t ^ , t ) = ⎣ ⎢ ⎡ 2 ( q 2 q 4 − q 1 q 3 ) 2 ( q 1 q 2 + q 3 q 4 ) ( q 1 2 − q 2 2 − q 3 2 + q 4 2 ) ⎦ ⎥ ⎤ e t + 1 = I a t + 1 ^ × v ( I W q e s t ^ , t ) e i , t + 1 = e i , t + e t + 1 Δ t
Δ t \Delta t Δ t
如果有一个复数 z = a + b i z = a + bi z = a + b i z z z c c c c c c θ = a t a n 2 ( b , a ) θ = atan2(b, a) θ = a t a n 2 ( b , a ) ∣ z ∣ = a 2 + b 2 |z| = \sqrt{a^{2} + b^{2}} ∣ z ∣ = a 2 + b 2 ∣ z ∣ = 1 |z| =1 ∣ z ∣ = 1 z z z
z = [ c o s ( θ ) − s i n ( θ ) s i n ( θ ) c o s ( θ ) ] z = \begin{bmatrix}cos(\theta ) &-sin(\theta) \\ sin(\theta)& cos(\theta)\end{bmatrix}
z = [ c o s ( θ ) s i n ( θ ) − s i n ( θ ) c o s ( θ ) ]
则对应的旋转公式(矩阵型)如下:
v ′ = [ c o s ( θ ) − s i n ( θ ) s i n ( θ ) c o s ( θ ) ] v {v}' = \begin{bmatrix}cos(\theta ) &-sin(\theta) \\ sin(\theta)& cos(\theta)\end{bmatrix} v
v ′ = [ c o s ( θ ) s i n ( θ ) − s i n ( θ ) c o s ( θ ) ] v
其中 z 可以用复数形式来表示即z = x + y i z = x + yi z = x + y i z = c o s ( θ ) + s i n ( θ ) i z = cos(\theta) + sin(\theta)i z = c o s ( θ ) + s i n ( θ ) i
v ′ = z v = ( c o s ( θ ) + i s i n ( θ ) ) v {v}' = zv = (cos(\theta) + i sin(\theta))v
v ′ = z v = ( c o s ( θ ) + i s i n ( θ ) ) v
这是二维的情况,推广到 3D 空间中任意一个 v v v u u u θ θ θ
v ′ = c o s ( θ ) v + ( 1 − c o s ( θ ) ) ( u ⋅ v ) u + s i n ( θ ) ( u × v ) v′ = cos(θ)v + (1 − cos(θ))(u · v)u + sin(θ)(u × v)
v ′ = c o s ( θ ) v + ( 1 − c o s ( θ ) ) ( u ⋅ v ) u + s i n ( θ ) ( u × v )
接着给出四元数旋转公式任意向量 v v v u u u θ θ θ v ′ v′ v ′ v = [ 0 , v ] , q = [ c o s ( 1 2 θ ) , s i n ( 1 2 θ ) u ] v = [0, v],q = \begin{bmatrix}cos(\frac{1}{2}\theta ), sin(\frac{1}{2}\theta )u \end{bmatrix} v = [ 0 , v ] , q = [ c o s ( 2 1 θ ) , s i n ( 2 1 θ ) u ]
v ′ = q v q ∗ = q v q − 1 {v}' = qvq^{*} = qvq^{-1}
v ′ = q v q ∗ = q v q − 1
换句话说,如果我们有 q = [ c o s ( θ ) , s i n ( θ ) u ] q = [cos(θ), sin(θ)u] q = [ c o s ( θ ) , s i n ( θ ) u ] v ′ = q v q ∗ v′ = qvq^{*} v ′ = q v q ∗ v v v u u u 2 θ 2θ 2 θ v v v u u u θ θ θ v ′ v′ v ′ a = c o s ( 1 2 θ ) , b = s i n ( 1 2 θ ) u x , c = s i n ( 1 2 θ ) u y , d = s i n ( 1 2 θ ) u z a =cos(\frac{1}{2}\theta ), b = sin(\frac{1}{2}\theta )u_x, c = sin(\frac{1}{2}\theta )u_y, d = sin(\frac{1}{2}\theta )u_z a = c o s ( 2 1 θ ) , b = s i n ( 2 1 θ ) u x , c = s i n ( 2 1 θ ) u y , d = s i n ( 2 1 θ ) u z
v ′ = [ 1 − 2 c 2 − 2 d 2 2 b c − 2 a d 2 a c + 2 b d 2 b c + 2 a d 1 − 2 b 2 − 2 d 2 2 c d − 2 a b 2 b d − 2 a c 2 a d + 2 c d 1 − 2 b 2 − 2 c 2 ] v {v}' = \begin{bmatrix}1-2c^2-2d^2 & 2bc - 2ad & 2ac+2bd \\ 2bc+2ad & 1-2b^2-2d^2 &2cd - 2ab \\ 2bd-2ac & 2ad+2cd & 1-2b^2-2c^2 \end{bmatrix}v
v ′ = ⎣ ⎢ ⎡ 1 − 2 c 2 − 2 d 2 2 b c + 2 a d 2 b d − 2 a c 2 b c − 2 a d 1 − 2 b 2 − 2 d 2 2 a d + 2 c d 2 a c + 2 b d 2 c d − 2 a b 1 − 2 b 2 − 2 c 2 ⎦ ⎥ ⎤ v
其中这里的四元数是归一化四元数即1 = q 1 2 + q 2 2 + q 3 2 + q 4 2 1 = q_1^2 + q_2^2 + q_3^2 + q_4^2 1 = q 1 2 + q 2 2 + q 3 2 + q 4 2
v = [ q 1 2 + q 2 2 − q 3 2 − q 4 2 2 ( q 2 q 3 − q 1 q 4 ) 2 ( q 2 q 4 + q 1 q 3 ) 2 ( q 2 q 3 + q 1 q 4 ) q 1 2 − q 2 2 + q 3 2 − q 4 2 2 ( q 3 q 4 − q 1 q 2 ) 2 ( q 2 q 4 − q 1 q 3 ) 2 ( q 3 q 4 + q 1 q 2 ) q 1 2 − q 2 2 − q 3 2 + q 4 2 ] v v = \begin{bmatrix}q_1^2 + q_2^2 -q_3^2 -q_4^2 &2(q_2q_3 - q_1q_4) &2(q_2q_4 + q_1q_3) \\ 2(q_2q_3 + q_1q_4) & q_1^2 - q_2^2 + q_3^2 -q_4^2 & 2(q_3q_4 - q_1q_2) \\ 2(q_2q_4 - q_1q_3)& 2(q_3q_4 + q_1q_2) & q_1^2 - q_2^2 -q_3^2 +q_4^2 \end{bmatrix}v
v = ⎣ ⎢ ⎡ q 1 2 + q 2 2 − q 3 2 − q 4 2 2 ( q 2 q 3 + q 1 q 4 ) 2 ( q 2 q 4 − q 1 q 3 ) 2 ( q 2 q 3 − q 1 q 4 ) q 1 2 − q 2 2 + q 3 2 − q 4 2 2 ( q 3 q 4 + q 1 q 2 ) 2 ( q 2 q 4 + q 1 q 3 ) 2 ( q 3 q 4 − q 1 q 2 ) q 1 2 − q 2 2 − q 3 2 + q 4 2 ⎦ ⎥ ⎤ v
这里其实是省略了相关推导,其中的详细推导过程我会在下面给出链接,这里我们直接使用这些已知的结论,不然东西太多,看着太累(其实是写起来太累)。到这里其实只是列出了四元数的旋转公式,好回到前面第二步中我们那个公式是怎么来的呢,下面看机体坐标系下的重力表示,将机体坐标系的三轴分量通过旋转矩阵的旋转后就是地理坐标系下的重力分量表示。而我们这里的旋转矩阵是正交矩阵即 M ∗ M T = I M*M^T = I M ∗ M T = I g = M ∗ g ^ g = M*\hat{g} g = M ∗ g ^ g ^ = M T ∗ g \hat{g} = M^T * g g ^ = M T ∗ g
g ^ = [ q 1 2 + q 2 2 − q 3 2 − q 4 2 2 ( q 2 q 3 − q 1 q 4 ) 2 ( q 2 q 4 + q 1 q 3 ) 2 ( q 2 q 3 + q 1 q 4 ) q 1 2 − q 2 2 + q 3 2 − q 4 2 2 ( q 3 q 4 − q 1 q 2 ) 2 ( q 2 q 4 − q 1 q 3 ) 2 ( q 3 q 4 + q 1 q 2 ) q 1 2 − q 2 2 − q 3 2 + q 4 2 ] ′ ∗ [ 0 0 1 ] = [ 2 ( q 2 q 4 − q 1 q 3 ) 2 ( q 3 q 4 + q 1 q 2 ) q 1 2 − q 2 2 − q 3 2 + q 4 2 ] \begin{aligned}
\hat{g} &= \begin{bmatrix}q_1^2 + q_2^2 -q_3^2 -q_4^2 &2(q_2q_3 - q_1q_4) &2(q_2q_4 + q_1q_3) \\ 2(q_2q_3 + q_1q_4) & q_1^2 - q_2^2 + q_3^2 -q_4^2 & 2(q_3q_4 - q_1q_2) \\ 2(q_2q_4 - q_1q_3)&2(q_3q_4 + q_1q_2) & q_1^2 - q_2^2 -q_3^2 +q_4^2 \end{bmatrix}' * \begin{bmatrix}0\\ 0\\ 1\end{bmatrix} \\
&=\begin{bmatrix}2(q_2q_4 - q_1q_3)\\ 2(q_3q_4 + q_1q_2)\\ q_1^2 - q_2^2 -q_3^2 +q_4^2\end{bmatrix}
\end{aligned}
g ^ = ⎣ ⎢ ⎡ q 1 2 + q 2 2 − q 3 2 − q 4 2 2 ( q 2 q 3 + q 1 q 4 ) 2 ( q 2 q 4 − q 1 q 3 ) 2 ( q 2 q 3 − q 1 q 4 ) q 1 2 − q 2 2 + q 3 2 − q 4 2 2 ( q 3 q 4 + q 1 q 2 ) 2 ( q 2 q 4 + q 1 q 3 ) 2 ( q 3 q 4 − q 1 q 2 ) q 1 2 − q 2 2 − q 3 2 + q 4 2 ⎦ ⎥ ⎤ ′ ∗ ⎣ ⎢ ⎡ 0 0 1 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 2 ( q 2 q 4 − q 1 q 3 ) 2 ( q 3 q 4 + q 1 q 2 ) q 1 2 − q 2 2 − q 3 2 + q 4 2 ⎦ ⎥ ⎤
这就是上面我们第二步中的公式,在自然坐标系下的机体三轴表示。写成代码就是如下:
1 2 3 4 5 // Estimated direction of gravity and vector perpendicular to magnetic flux halfvx = imu->q1 * imu->q3 - imu->q0 * imu->q2; halfvy = imu->q0 * imu->q1 + imu->q2 * imu->q3; //halfvz = imu->q0 * imu->q0 - 0.5f + imu->q3 * imu->q3; halfvz = imu->q0 * imu->q0 - imu->q1 * imu->q1 - imu->q2 * imu->q2 + imu->q3 * imu->q3;
这第二步还没完,后面还两个公式呢,先看第一个公式
e t + 1 = I a t + 1 ^ × v ( I W q e s t ^ , t ) e_{t+1} = I_{\hat{a_{t+1}}} \times v(\hat{_{I}^{W}\textrm{}q_{est}},t)
e t + 1 = I a t + 1 ^ × v ( I W q e s t ^ , t )
这一步将加速度计获取的数据与陀螺仪准确来讲是预测值进行叉乘,来表示陀螺仪与加速度计的误差,这里为什么可以通过叉乘得到误差呢,其实是存疑的,向量的叉乘结果跟两个向量的夹角和模长相关,这里 acc 与 gyro 的数据如果是相同的那么他们之间的夹角为 0 则 s i n ( θ ) = 0 sin(\theta) = 0 s i n ( θ ) = 0 z 1 = a + b i z 2 = c + d i z_1 = a + bi z_2 = c + di z 1 = a + b i z 2 = c + d i
z 1 × z 2 = [ a − b b a ] × [ c − d d c ] = [ a c − b d − ( b c + a d ) b c + a d a c − b d ] \begin{aligned}
z_1\times z_2 &= \begin{bmatrix}a &-b \\ b & a\end{bmatrix} \times \begin{bmatrix}c &-d \\ d & c\end{bmatrix} \\
&= \begin{bmatrix}ac-bd &-(bc + ad) \\ bc + ad & ac-bd\end{bmatrix}
\end{aligned}
z 1 × z 2 = [ a b − b a ] × [ c d − d c ] = [ a c − b d b c + a d − ( b c + a d ) a c − b d ]
写为代码就是下面:
1 2 3 4 // Error is sum of cross product between estimated and measured direction of gravity halfex = (ay * halfvz - az * halfvy); halfey = (az * halfvx - ax * halfvz); halfez = (ax * halfvy - ay * halfvx);
第三个公式就比较简单了对误差进行累计,这里代码跟下面第三步放到一起。第二步完。…
I w t + 1 = I w t + 1 + K p ∗ e t + 1 K i ∗ e i , t + 1 I{w_{t+1}} = I{w_{t+1}} + K_p * e_{t+1} K_i * e_{i,t+1}
I w t + 1 = I w t + 1 + K p ∗ e t + 1 K i ∗ e i , t + 1
这个公式对于比较熟悉 pid 算法的人来讲应该是轻而易举的事了吧,关于 pid 调节这里也不是一两句话可以说的清楚的,后面专门再写一篇关于 pid 调节的文章吧,后续一定会用到的,这里先偷下懒,通俗点将这里就是对误差进行一个比例扩大或缩小即误差的积分累计运算,这个量会用于调节陀螺仪的数据,以纠正陀螺仪的累计误差让陀螺仪的数据最终收敛于加速度计数据。照例贴下代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 // Compute and apply integral feedback if enabled if (twoKi > 0.0f) { imu->integralFBx += twoKi * halfex * (1.0f / sampleFreq); // integral error scaled by Ki imu->integralFBy += twoKi * halfey * (1.0f / sampleFreq); imu->integralFBz += twoKi * halfez * (1.0f / sampleFreq); gx += imu->integralFBx; // apply integral feedback gy += imu->integralFBy; gz += imu->integralFBz; } else { imu->integralFBx = 0.0f; // prevent integral windup imu->integralFBy = 0.0f; imu->integralFBz = 0.0f; } // Apply proportional feedback gx += twoKp * halfex; gy += twoKp * halfey; gz += twoKp * halfez;
前面我们对姿态角的变化量加速度进行 pi 调节器的调节后(使其收敛于加速度计计算的重力向量)就可以进行积分了,其积分就涉及到微分方程的求解和运算,下面会给出推导步骤如下:
四元数微分方程n n n b b b n n n b b b
Q = c o s ( 1 2 θ ) + s i n ( 1 2 θ ) u n Q = cos( \frac{1}{2}\theta ) + sin(\frac{1}{2}\theta )u^n
Q = c o s ( 2 1 θ ) + s i n ( 2 1 θ ) u n
其中u n u^n u n Q = c o s ( 1 2 θ ) + s i n ( 1 2 θ ) u Q = cos(\frac{1}{2}\theta ) + sin(\frac{1}{2}\theta )u Q = c o s ( 2 1 θ ) + s i n ( 2 1 θ ) u
Q = c o s ( 1 2 θ ) + s i n ( 1 2 θ ) u n d Q d t = − 1 2 s i n ( 1 2 θ ) ⋅ d θ d t + d u n d t ⋅ s i n ( 1 2 θ ) + u n ⋅ 1 2 c o s ( 1 2 θ ) ⋅ d θ d t Q = cos(\frac{1}{2}\theta ) + sin(\frac{1}{2}\theta )u^n \\
\frac{dQ}{dt} = -\frac{1}{2}sin(\frac{1}{2}\theta )\cdot \frac{d\theta }{dt} + \frac{du^n}{dt}\cdot sin(\frac{1}{2}\theta ) + u^n \cdot \frac{1}{2}cos(\frac{1}{2}\theta )\cdot \frac{d\theta }{dt}
Q = c o s ( 2 1 θ ) + s i n ( 2 1 θ ) u n d t d Q = − 2 1 s i n ( 2 1 θ ) ⋅ d t d θ + d t d u n ⋅ s i n ( 2 1 θ ) + u n ⋅ 2 1 c o s ( 2 1 θ ) ⋅ d t d θ
其中这是一个旋转四元数,其旋转轴是固定不变的,变化的是旋转角度,因此 d u n d t = 0 \frac{du^n}{dt} = 0 d t d u n = 0
d Q d t = − 1 2 s i n ( 1 2 θ ) ⋅ d θ d t + u n ⋅ 1 2 c o s ( 1 2 θ ) ⋅ d θ d t \frac{dQ}{dt} = -\frac{1}{2}sin(\frac{1}{2}\theta ) \cdot \frac{d\theta }{dt} + u^n \cdot \frac{1}{2}cos(\frac{1}{2}\theta )\cdot \frac{d\theta }{dt}
d t d Q = − 2 1 s i n ( 2 1 θ ) ⋅ d t d θ + u n ⋅ 2 1 c o s ( 2 1 θ ) ⋅ d t d θ
两边都乘以 1 2 u n d θ d t \frac{1}{2} u^n \frac{d\theta }{dt} 2 1 u n d t d θ
1 2 u n d θ d t ⊗ Q = 1 2 u n d θ d t ∗ ( c o s ( θ 2 ) + s i n ( θ 2 ) u n ) = θ ˙ 2 c o s ( θ 2 ) u n + u n ⊗ u n θ ˙ 2 s i n ( θ 2 ) r \begin{aligned}
\frac{1}{2} u^n \frac{d\theta }{dt} \otimes Q &= \frac{1}{2} u^n \frac{d\theta }{dt} * (cos(\frac{\theta }{2}) + sin(\frac{\theta }{2}) u^n) \\
& = \frac{\dot{\theta }}{2}cos(\frac{\theta }{2})u^n + u^n \otimes u^n \frac{\dot{\theta }}{2}sin(\frac{\theta }{2})r
\end{aligned}
2 1 u n d t d θ ⊗ Q = 2 1 u n d t d θ ∗ ( c o s ( 2 θ ) + s i n ( 2 θ ) u n ) = 2 θ ˙ c o s ( 2 θ ) u n + u n ⊗ u n 2 θ ˙ s i n ( 2 θ ) r
其中 $u^n \otimes u^n = -1 $ 得:
1 2 u n d θ d t ⊗ Q = θ ˙ 2 c o s ( θ 2 ) u n − θ ˙ 2 s i n ( θ 2 ) r \begin{aligned}
\frac{1}{2} u^n \frac{d\theta }{dt} \otimes Q = \frac{\dot{\theta }}{2}cos(\frac{\theta }{2})u^n - \frac{\dot{\theta }}{2}sin(\frac{\theta }{2})r
\end{aligned}
2 1 u n d t d θ ⊗ Q = 2 θ ˙ c o s ( 2 θ ) u n − 2 θ ˙ s i n ( 2 θ ) r
这个结果与上面推导的 d Q d t \frac{dQ}{dt} d t d Q d Q d t \frac{dQ}{dt} d t d Q
d Q d t = 1 2 u n d θ d t ⊗ Q = 1 2 w n b n ⊗ Q \frac{dQ}{dt} = \frac{1}{2} u^n \frac{d\theta }{dt} \otimes Q = \frac{1}{2} w_{nb}^{n}\otimes Q
d t d Q = 2 1 u n d t d θ ⊗ Q = 2 1 w n b n ⊗ Q
式中 w n b n w_{nb}^{n} w n b n
r n = Q ⊗ r b ⊗ Q ∗ r^n = Q \otimes r^b \otimes Q^*
r n = Q ⊗ r b ⊗ Q ∗
带入上式得:
d Q d t = 1 2 Q ⊗ w n b b ⊗ Q ∗ ⊗ Q \frac{dQ}{dt} = \frac{1}{2} Q \otimes w_{nb}^{b} \otimes Q^* \otimes Q
d t d Q = 2 1 Q ⊗ w n b b ⊗ Q ∗ ⊗ Q
对于单位四元数有:Q ∗ ⊗ Q = 1 Q^* \otimes Q = 1 Q ∗ ⊗ Q = 1
d Q d t = 1 2 Q ⊗ w n b b \frac{dQ}{dt} = \frac{1}{2} Q \otimes w_{nb}^b
d t d Q = 2 1 Q ⊗ w n b b
其中 w n b b w_{nb}^{b} w n b b
w n b b = [ 0 w x w y w z ] w_{nb}^{b} = \begin{bmatrix}0\\ w_x\\ w_y\\ w_z\end{bmatrix}
w n b b = ⎣ ⎢ ⎢ ⎢ ⎡ 0 w x w y w z ⎦ ⎥ ⎥ ⎥ ⎤
由四元数乘法公式可以得到:
[ q 0 ˙ q 1 ˙ q 2 ˙ q 3 ˙ ] = 1 2 [ q 0 − q 1 − q 2 − q 3 q 1 q 0 − q 3 q 2 q 2 q 3 q 0 − q 1 q 3 − q 2 q 1 q 0 ] ∗ [ 0 w x w y w z ] \begin{bmatrix}
\dot{q_0}\\ \dot{q_1}\\ \dot{q_2}\\ \dot{q_3}\end{bmatrix} = \frac{1}{2}\begin{bmatrix}
q_0 & -q_1 & -q_2 & -q_3 \\
q_1 & q_0 & -q_3 & q_2 \\
q_2 & q_3 & q_0 & -q_1 \\
q_3 & -q_2 & q_1 & q_0
\end{bmatrix} * \begin{bmatrix}{0}\\ w_x\\ {w_y}\\ {w_z}\end{bmatrix}
⎣ ⎢ ⎢ ⎢ ⎡ q 0 ˙ q 1 ˙ q 2 ˙ q 3 ˙ ⎦ ⎥ ⎥ ⎥ ⎤ = 2 1 ⎣ ⎢ ⎢ ⎢ ⎡ q 0 q 1 q 2 q 3 − q 1 q 0 q 3 − q 2 − q 2 − q 3 q 0 q 1 − q 3 q 2 − q 1 q 0 ⎦ ⎥ ⎥ ⎥ ⎤ ∗ ⎣ ⎢ ⎢ ⎢ ⎡ 0 w x w y w z ⎦ ⎥ ⎥ ⎥ ⎤
或者:
[ q 0 ˙ q 1 ˙ q 2 ˙ q 3 ˙ ] = 1 2 [ 0 − w x − w y − w z w x 0 w z − w y w y − w z 0 w x w z w y − w x 0 ] ∗ [ q 0 q 1 q 2 q 3 ] \begin{bmatrix}\dot{q_0}\\ \dot{q_1}\\ \dot{q_2}\\ \dot{q_3}\end{bmatrix} = \frac{1}{2}\begin{bmatrix}
0 & -w_x & -w_y& -w_z \\
w_x& 0 & w_z& -w_y \\
w_y& -w_z& 0 & w_x \\
w_z& w_y& -w_x& 0
\end{bmatrix} * \begin{bmatrix}{q_0}\\ q_1\\ {q_2}\\ {q_3}\end{bmatrix}
⎣ ⎢ ⎢ ⎢ ⎡ q 0 ˙ q 1 ˙ q 2 ˙ q 3 ˙ ⎦ ⎥ ⎥ ⎥ ⎤ = 2 1 ⎣ ⎢ ⎢ ⎢ ⎡ 0 w x w y w z − w x 0 − w z w y − w y w z 0 − w x − w z − w y w x 0 ⎦ ⎥ ⎥ ⎥ ⎤ ∗ ⎣ ⎢ ⎢ ⎢ ⎡ q 0 q 1 q 2 q 3 ⎦ ⎥ ⎥ ⎥ ⎤
剩下的就是求解四元数微分方程了,求解方法有欧拉方法、毕卡算法,龙格库塔法,其中常用的是龙格库塔法求解,采用一阶龙格库塔法解算过程如下:y n + 1 = y n + h ⋅ y ′ y_{n+1} = y_n + h \cdot y^{'} y n + 1 = y n + h ⋅ y ′
Q ( t + △ t ) = Q ( t ) + △ t d Q d t Q(t+\triangle t) = Q(t) + \triangle t \frac{dQ}{dt}
Q ( t + △ t ) = Q ( t ) + △ t d t d Q
故可以得到:
[ q 0 q 1 q 2 q 3 ] t + △ t = [ q 0 q 1 q 2 q 3 ] t + △ t 2 ∗ [ 0 − w x − w y − w z w x 0 w z − w y w y − w z 0 w x w z w y − w x 0 ] ∗ [ q 0 q 1 q 2 q 3 ] t \begin{bmatrix}{q_0}\\ q_1\\ {q_2}\\ {q_3}\end{bmatrix}_{t+\triangle t } = \begin{bmatrix}{q_0}\\ q_1\\ {q_2}\\ {q_3}\end{bmatrix}_{t } + \frac{\triangle t }{2} * \begin{bmatrix}
0 & -w_x & -w_y& -w_z \\
w_x& 0 & w_z& -w_y \\
w_y& -w_z& 0 & w_x \\
w_z& w_y& -w_x& 0
\end{bmatrix} * \begin{bmatrix}{q_0}\\ q_1\\ {q_2}\\ {q_3}\end{bmatrix}_{t}
⎣ ⎢ ⎢ ⎢ ⎡ q 0 q 1 q 2 q 3 ⎦ ⎥ ⎥ ⎥ ⎤ t + △ t = ⎣ ⎢ ⎢ ⎢ ⎡ q 0 q 1 q 2 q 3 ⎦ ⎥ ⎥ ⎥ ⎤ t + 2 △ t ∗ ⎣ ⎢ ⎢ ⎢ ⎡ 0 w x w y w z − w x 0 − w z w y − w y w z 0 − w x − w z − w y w x 0 ⎦ ⎥ ⎥ ⎥ ⎤ ∗ ⎣ ⎢ ⎢ ⎢ ⎡ q 0 q 1 q 2 q 3 ⎦ ⎥ ⎥ ⎥ ⎤ t
写为代码如下:
1 2 3 4 5 6 7 8 9 10 11 // Integrate rate of change of quaternion gx *= (0.5f * (1.0f / sampleFreq)); // pre-multiply common factors gy *= (0.5f * (1.0f / sampleFreq)); gz *= (0.5f * (1.0f / sampleFreq)); qa = q0; qb = q1; qc = q2; q0 += (-qb * gx - qc * gy - q3 * gz); q1 += (qa * gx + qc * gz - q3 * gy); q2 += (qa * gy - qb * gz + q3 * gx); q3 += (qa * gz + qb * gy - qc * gx);
最后再对四元数进行归一化,如下:
1 2 3 4 5 6 // Normalise quaternion recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3); q0 *= recipNorm; q1 *= recipNorm; q2 *= recipNorm; q3 *= recipNorm;
至此所有理论推导都完成了,剩下的就是不停的循环上面的步骤就得到了四元数,剩下的任务就是将四元数转为欧拉角了,这里转欧拉角里面也是有坑的,需要考虑欧拉角的奇异性,在转化的过程中要注意对欧拉角的奇异性进行考虑就可以了。
http://file.elecfans.com/web1/M00/7F/89/o4YBAFwnoJ2AGdjpACAXh7JE-_I005.pdf https://krasjet.github.io/quaternion/quaternion.pdf https://zhuanlan.zhihu.com/p/103623879 https://zhuanlan.zhihu.com/p/55681807 https://x-io.co.uk/open-source-imu-and-ahrs-algorithms/ https://nitinjsanket.github.io/tutorials/attitudeest/mahony http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/ https://github.com/CarlyleLiu/KalmanFilter



)


