源码

SVM 函数的 alpha 和 beta 的值是经过了标幺化，基准值为 （最大相电压），也就是说 alpha 和 beta 的范围是 [-1,1]。约束：alpha-beta 向量的大小不得大于 $ \frac{\sqrt{3}}{2} $。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
// Compute rising edge timings (0.0 - 1.0) as a function of alpha-beta
// as per the magnitude invariant clarke transform
// The magnitude of the alpha-beta vector may not be larger than sqrt(3)/2
// Returns true on success, and false if the input was out of range
std::tuple<float, float, float, bool> SVM(float alpha, float beta) {
    float tA, tB, tC;
    int Sextant;

    if (beta >= 0.0f) {
        if (alpha >= 0.0f) {
            //quadrant I
            if (one_by_sqrt3 * beta > alpha)
                Sextant = 2; //sextant v2-v3
            else
                Sextant = 1; //sextant v1-v2
        } else {
            //quadrant II
            if (-one_by_sqrt3 * beta > alpha)
                Sextant = 3; //sextant v3-v4
            else
                Sextant = 2; //sextant v2-v3
        }
    } else {
        if (alpha >= 0.0f) {
            //quadrant IV
            if (-one_by_sqrt3 * beta > alpha)
                Sextant = 5; //sextant v5-v6
            else
                Sextant = 6; //sextant v6-v1
        } else {
            //quadrant III
            if (one_by_sqrt3 * beta > alpha)
                Sextant = 4; //sextant v4-v5
            else
                Sextant = 5; //sextant v5-v6
        }
    }

    switch (Sextant) {
        // sextant v1-v2
        case 1: {
            // Vector on-times
            float t1 = alpha - one_by_sqrt3 * beta;
            float t2 = two_by_sqrt3 * beta;

            // PWM timings
            tA = (1.0f - t1 - t2) * 0.5f;
            tB = tA + t1;
            tC = tB + t2;
        } break;

        // sextant v2-v3
        case 2: {
            // Vector on-times
            float t2 = alpha + one_by_sqrt3 * beta;
            float t3 = -alpha + one_by_sqrt3 * beta;

            // PWM timings
            tB = (1.0f - t2 - t3) * 0.5f;
            tA = tB + t3;
            tC = tA + t2;
        } break;

        // sextant v3-v4
        case 3: {
            // Vector on-times
            float t3 = two_by_sqrt3 * beta;
            float t4 = -alpha - one_by_sqrt3 * beta;

            // PWM timings
            tB = (1.0f - t3 - t4) * 0.5f;
            tC = tB + t3;
            tA = tC + t4;
        } break;

        // sextant v4-v5
        case 4: {
            // Vector on-times
            float t4 = -alpha + one_by_sqrt3 * beta;
            float t5 = -two_by_sqrt3 * beta;

            // PWM timings
            tC = (1.0f - t4 - t5) * 0.5f;
            tB = tC + t5;
            tA = tB + t4;
        } break;

        // sextant v5-v6
        case 5: {
            // Vector on-times
            float t5 = -alpha - one_by_sqrt3 * beta;
            float t6 = alpha - one_by_sqrt3 * beta;

            // PWM timings
            tC = (1.0f - t5 - t6) * 0.5f;
            tA = tC + t5;
            tB = tA + t6;
        } break;

        // sextant v6-v1
        case 6: {
            // Vector on-times
            float t6 = -two_by_sqrt3 * beta;
            float t1 = alpha + one_by_sqrt3 * beta;

            // PWM timings
            tA = (1.0f - t6 - t1) * 0.5f;
            tC = tA + t1;
            tB = tC + t6;
        } break;
    }

    bool result_valid =
            tA >= 0.0f && tA <= 1.0f
         && tB >= 0.0f && tB <= 1.0f
         && tC >= 0.0f && tC <= 1.0f;
    return {tA, tB, tC, result_valid};
}

函数主体上可以分为 2 大块，第一大块是个复合的 if 语句，用于判断扇区，第二个则是个 switch 语句，用于计算定时器的比较值，用于产生不同占空比的 PWM。

扇区判断

对于第一部分扇区判断，以第 1 扇区为例说明。

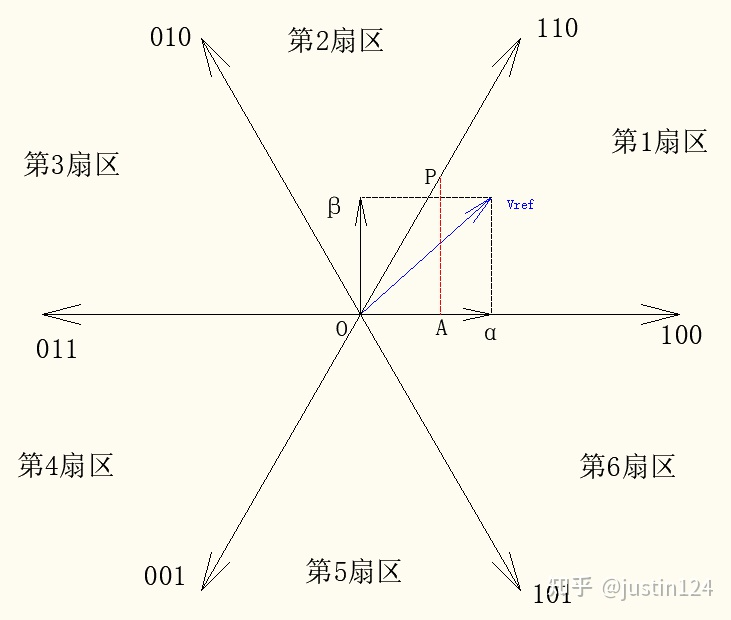
如图 1 所示，给定的$ \alpha \beta 值使得其合向量蓝色的值使得其合向量蓝色的vref位于第1扇区。分析一下位于第1扇区的位于第 1 扇区。分析一下位于第 1 扇区的 \alpha \beta 有什么特点，最明显的就是，但这应该是位于第一象限的特点，还有30°的范围不属于第1扇区，继续分析。每个扇区都是60°，因此可以通过三角函数来确定有什么特点，最明显的就是 ，但这应该是位于第一象限的特点，还有 30°的范围不属于第 1 扇区，继续分析。每个扇区都是 60°，因此可以通过三角函数来确定 \alpha 和和 \beta 的关系。过110轴上任意点P做100轴的垂线PA，则ΔOPA显然为直角三角形，且∠PAO=90°，∠POA=60°，∠OPA=30°，此时，正好是的关系。过 110 轴上任意点 P 做 100 轴的垂线 PA，则ΔOPA 显然为直角三角形，且∠PAO=90°，∠POA=60°，∠OPA=30°，此时，正好是 \alpha \beta 的合向量恰好位于110轴的情形，当的合向量恰好位于 110 轴的情形，当\beta的值略小或的值略小或\alpha$的值略大时，∠POA 都将小于 60°，合向量落入第 1 扇区。从数学上说

∠POA=arctanPAOA=arctanβα<60°\angle POA = arctan \frac{PA}{ OA} = arctan \frac{\beta}{ \alpha} < 60°

即可作为 1 扇区判断条件，坏消息是 arctan 在 MCU 上计算得慢，所以得换换思路。

tan∠POA=βαtan \angle POA = \frac{\beta}{ \alpha}

这是一个显而易见的结论，当合向量恰好位于 110 轴时$ tan60° = \frac{\beta}{ \alpha} $ ，也就是$ \beta = \sqrt{3} \alpha$ ，如果和程序中的表述一致的话，就是α=13β\alpha = \frac{1}{ \sqrt{3}} \beta 。当β\beta减小α\alpha不变或α\alpha增大β\beta不变时，合向量都将从 110 轴转向 1 扇区，反之则转入 2 扇区。

综上所述得到结论，当$\alpha > 0, \beta > 0 $ 且 β>3α\beta > \sqrt{3} \alpha 合向量落在第 1 扇区； 当$\alpha > 0, \beta > 0 $ 且 β<3α\beta < \sqrt{3} \alpha，合向量落在第 2 扇区。

PWM 值计算

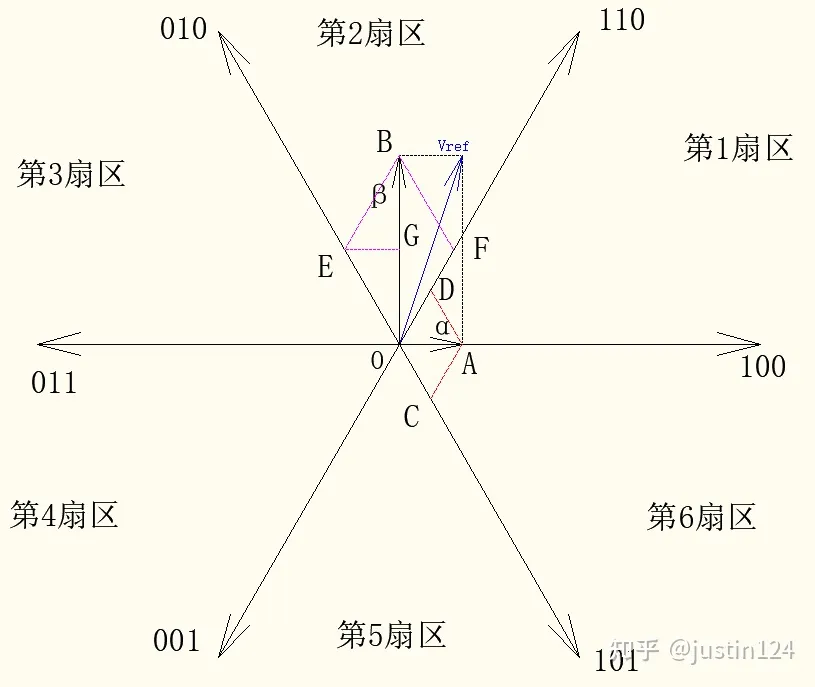
接下来聊一聊 PWM 比较值是如何计算的，这次以第 2 扇区为例，如图 2 所示。

在第 2 扇区的合向量是需要借助 010 和 110 这两个基本向量合成得到，传入 SVM 函数的参数 alpha 和 beta 的合向量是VrefVref。然后考虑将 α\alpha 和β\beta的值都分解到 010 和 110 这两个基本向量上。将α\alpha 在 100 轴的端点称为 A 点，β\beta端点称为 B 点。

先试着分解α\alpha向量，过 A 点作 110（001）轴的平行线交 101 轴于 C 点。过 A 点作 010（101）轴平行线交 110 轴于 D 点。分析易得$ \bigtriangleup OAC \bigtriangleup OAD$ 都是等边三角形。因此，α\alpha向量分解到 110 轴的长度也是α\alpha，分解到 010 轴的长度是−α- \alpha。

然后分解β\beta向量，过 B 点作 110 轴平行线交 010 轴于 E 点，过 B 点作 010 轴平行线交 110 轴于 F 点。易分析得 △OBE、△OBF\bigtriangleup OBE 、 \bigtriangleup OBF 为底角为 30°的等腰三角形，需求 OE 和 OF 长度，且 OE=OF=BF=BE。过 E 点作 OB 垂线交于 G，则 △EGB\bigtriangleup EGB为直角三角形，且∠EBG=30°\angle EBG = 30° 则BE=23BGBE = \frac{2}{\sqrt{3}} BG 而BG=12βBG = \frac{1}{2} \beta 故BE=13βBE = \frac{1}{\sqrt{3}} \beta 为所求。
可以给结论了，110 轴上产生作用力的时间定义为 t2，010 轴上产生作用力的时间定义为 t3。则有：

t3=−α+13βt3 = - \alpha + \frac{1}{\sqrt{3}} \beta

t2=α+13βt2 = \alpha + \frac{1}{\sqrt{3}} \beta

odriver speed [[odriverSpeed]]

参考文献

https://zhuanlan.zhihu.com/p/506240030
[[odriverSpeed]]