相机校准模型

小孔成像模型

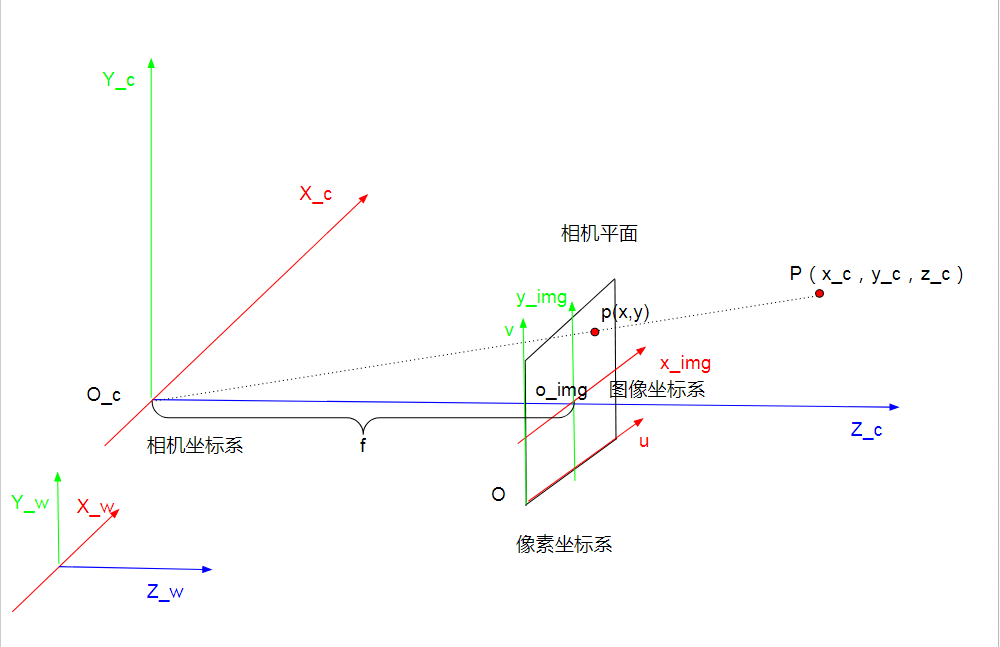
各坐标系定义及相机的内参和外参

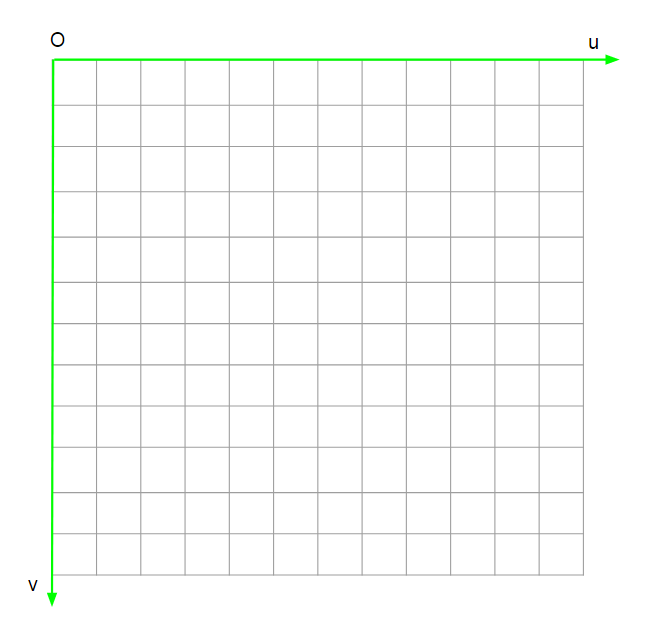
像素坐标系

像素坐标就是像素在图像中的位置。一般像素坐标系的左上角的顶点就是原点，水平向右是 u，垂直向下是 v 轴。

图像坐标系

在像素坐标系中，每个像素的坐标是用像素来表示的，然而，像素的表示方法却不能反应图像中物体的物理尺寸，因此，有必要将像素坐标转换为图像坐标。将像素坐标系的原点平移到图像的中心，就定为图像坐标系的原点，图像坐标系的 x 轴与像素坐标系的 u 轴平行，方向相同，而图像坐标系的 y 轴与像素坐标系的 v 轴平行，方向相同。

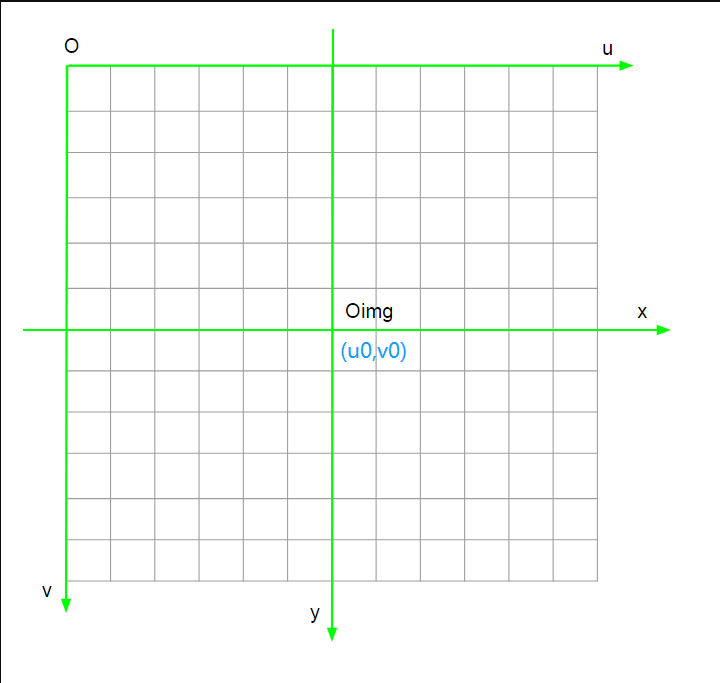
在图中，假设在像素坐标系下图像中心的像素坐标是（u0,v0），相机中感光器件每个像素的物理尺寸是 dx * dy，那么，图像坐标系的坐标（x,y）与像素坐标系的坐标（u,v）之间的关系可以表示为：

$$u = \frac{x}{d_x} + u_0 \\ v = \frac{y}{d_y} + v_0$$

写成矩阵的形式就为：

$$\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} \frac{1}{d_x} & 0 \\ 0 & \frac{1}{d_y} \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} u_0\\ v_0 \end{bmatrix}$$

改写为齐次坐标的形式：

$$\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{d_x}& 0 &0 \\ 0 & \frac{1}{d_y} & 0\\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ 0 \end{bmatrix} + \begin{bmatrix} u_o \\ v_o \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{d_x}& 0 &u_o \\ 0 & \frac{1}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$$

相机坐标系

相机坐标系是以相机的光轴作为 Z 轴，光线在相机光学系统的中心位置就是原点 Oc（实际上就是透镜的中心）, 相机坐标系的水平轴 Xc 与垂直轴 Yc 分别于图像坐标系的 X 轴和 Y 轴平行。在图中，相机坐标系的原点与图像坐标系的原点之间的距离 OcOi 之间的距离为 f（也就是焦距）。

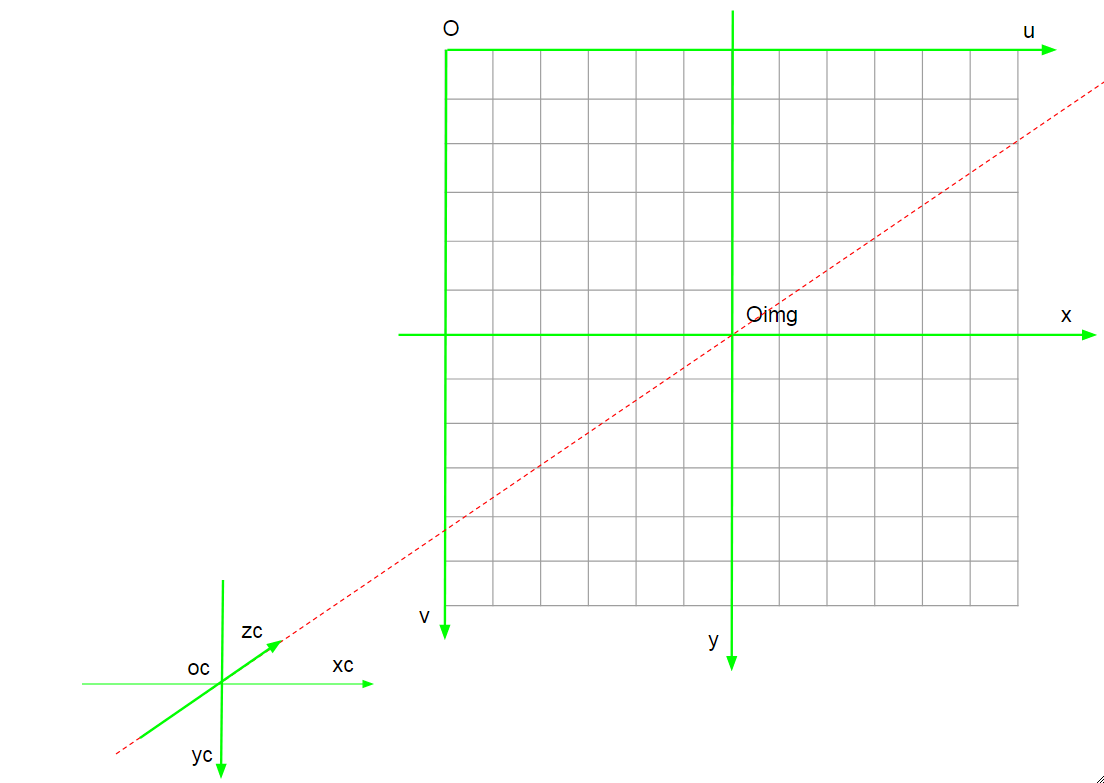
假设，三维空间中点 P, 其在相机坐标系下坐标为$P_c = [x_c,y_c,z_c]^T$; 其像点 p，在图像坐标系中坐标为。

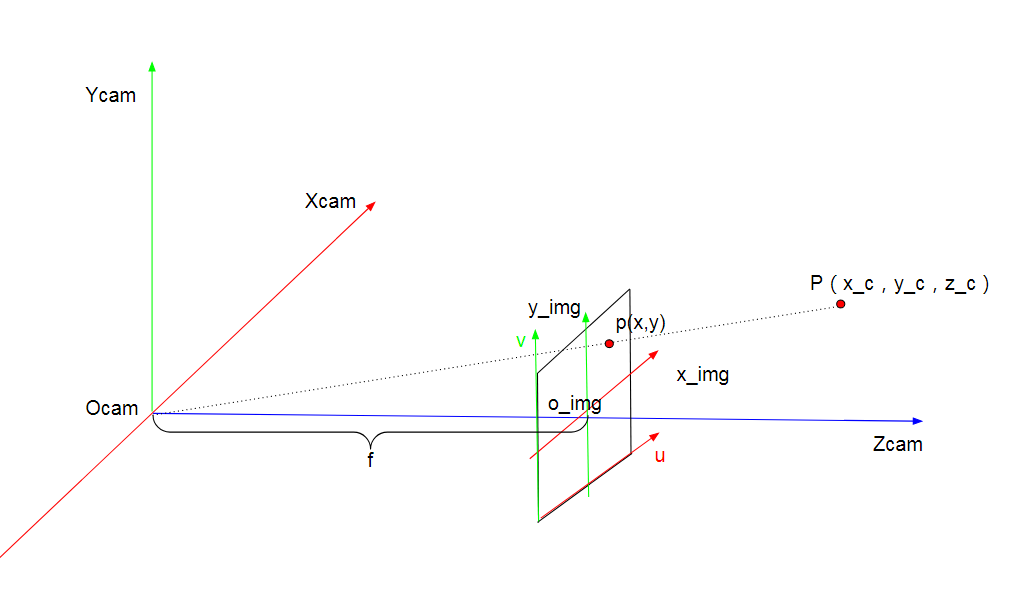
由相似三角形原理，得到

$$\frac{f}{z_c} = \frac{x}{x_c} = \frac{y}{y_c} \\ x = f \frac{x_c}{z_c}, y = f \frac{y_c}{z_c}$$

用向量表示为：

$$\begin{bmatrix} x\\ y\\ 1 \end{bmatrix} = \frac{1}{z_c}\begin{bmatrix} f &0  &0 \\  0 & f & 0\\  0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_c\\  y_c\\  z_c \end{bmatrix}$$

进一步可以写为：

$$\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{d_x}& 0 &u_o \\ 0 & \frac{1}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\  y \\ 1 \end{bmatrix} = \frac{1}{z_c}\begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_c\\  y_c\\  z_c \end{bmatrix}$$

到这里$\begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix}$ 就是相机的内参矩阵，跟相机的焦距和传感器的大小等参数有关。

世界坐标系

界坐标系是图像与真实物体之间的一个映射关系。如果是单目视觉的话，主要就是真实物体尺寸与图像尺寸的映射关系。如果是多目视觉的话，那么就需要知道多个相机之间的关系，这个关系就需要在同一个坐标系下进行换算。在下图中，世界坐标系的原点是 Ow, 而 Xw,Yw,Zw 轴并不是与其他坐标系平行的，而是有一定的角度，并且有一定的平移。

对于世界坐标系到相机坐标系的转换是刚体变换，是旋转动作和平移动作的结果，如下：

$$\begin{bmatrix} x_c\\  y_c\\  z_c\\  1 \end{bmatrix} = \begin{bmatrix}R & t\\ 0 & 1 \end{bmatrix}\begin{bmatrix} x_w\\  y_w\\  z_w\\  1 \end{bmatrix}$$

这里$\begin{bmatrix}R & t\\ 0 & 1 \end{bmatrix}$就是相机的外参矩阵，R 是相机相对世界坐标系的旋转关系，t 是相机相对于世界坐标系的平移关系，当相机位姿发生变化，该参数也相应的发生变化**。

图像畸变及畸变矫正

径向畸变

径向畸变：是由于透镜形状的制造工艺导致，且越向透镜边缘移动径向畸变越严重，实际情况中我们常用 r=0 处的泰勒级数展开的前几项来近似描述径向畸变，矫正径向畸变前后的坐标关系为：

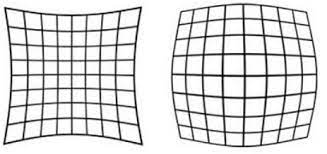
径向畸变的矫正公式如下：

$$\begin{aligned} &x_{rad}=x(1+k_1r^2+k_2r^4+k_3r^6) \\ &y_{rad}=y(1+k_1r^2+k_2r^4+k_3r^6) \end{aligned}$$

切向畸变

切向畸变：是由于透镜和 CMOS 或者 CCD 的安装位置误差导致，切向畸变需要两个额外的畸变参数来描述，矫正前后的坐标关系为：

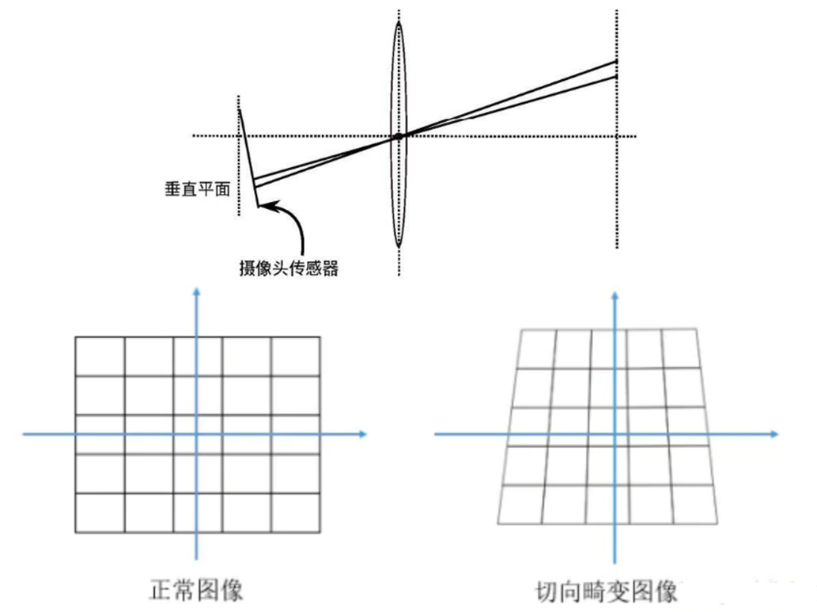
切向畸变的矫正公式如下（这里不给出推导过程，直接使用）：

$$x_{tan}=x+2p_1xy+p_2(r^2+2x^2)\\y_{tan}=y+p_1(r^2+2y^2)+2p_2xy$$

畸变矫正

综合以上两种畸变，得到相机的畸变模型（纠正后的图像像素坐标系的坐标）：

$$\begin{aligned} &r^2=x^2+y^2 \\ &x_{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)+2p_1xy+p_2(r^2+2x^2) \\ &y_{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6)+p_1(r^2+2y^2)+2p_2xy \end{aligned}$$

其中 x,y 是是去畸变后的图像坐标，它是归一化的坐标，以图像中心为原点。r 为半径。$x_{distorted}y_{distorted}$是具有畸变得图像坐标。