ISP YUV 域之 EdgeEnhancement
Retinex 理论
Retinex 这个词由 Retina 和 Cortex 两个单词组成。在 Retinex 理论中,物体的颜色是由物体对长波、中波和短波光线的反射能力决定的,而不是由反射光强度的绝对值决定的,并且物体的色彩不受光照非均性的影响,具有一致性。
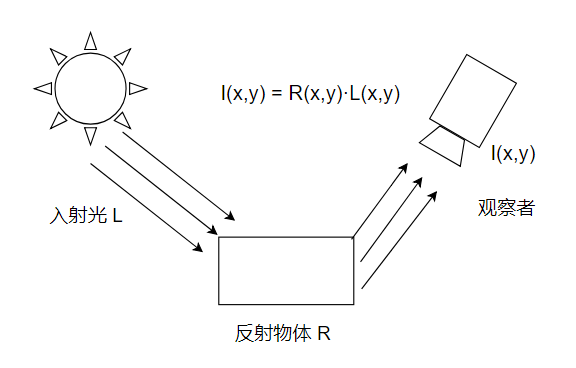
在 Retinex 理论中,人眼得到的图像数据取决于入射光和物体表面对入射光的反射。如上图所示,I(x,y) 是我们最终得到的图像数据,先是由入射光照射,然后经由物体反射进入成像系统,最终形成我们所看到的图像。该过程可以用公式表示:
其中,I(x,y) 代表被观察或照相机接收到的图像信号;L(x,y) 代表环境光的照射分量 ;R(x,y) 表示携带图像细节信息的目标物体的反射分量。将该式子两边取对数,可以得到物体原本的信息:
在图像处理领域,常将该理论用于图像增强,为了得到成像更好的图片。这时,R(x,y) 表示为图像增强得到后的图像,I(x,y) 为原始的图像。在处理过程中 L(x,y) 常为 I(x,y) 高通滤波之后的结果,也可以用其他滤波的方法,比如中值滤波,均值滤波等等。
SSR 算法
SSR (Singal Scale Retinex),即单尺度视网膜算法是 Retinex 算法中最基础的一个算法。运用的就是上面的方法,具体步骤如下:
- 输入原始图像 I(x,y) 和滤波的半径范围 sigma。
- 计算原始图像 I(x,y) 高斯滤波后的结果,得到 L(x,y)。
- 按照公式计算,得到 Log[R(x,y)]。
- 将得到的结果量化为 [0, 255] 范围的像素值,然后输出结果图像。
需要注意的是,最后一步量化的过程中,并不是将 Log[R(x,y)] 进行 Exp 化得到 R(x,y) 的结果,而是直接将 Log[R(x,y)] 的结果直接用如下公式进行量化:
将过程整合在一起就是如下过程:
G(x,y) 代表高斯核,Retinex 算法是去掉光照的影响,还原图像的本来面目。
MSR 算法
MSR 是在 SSR 基础上发展来的,优点是可以同时保持图像高保真度与对图像的动态范围进行压缩的同时,MSR 也可实现色彩增强、颜色恒常性、局部动态范围压缩、全局动态范围压缩,也可以用于 X 光图像增强。
为了得到更好的效果,人们又开发出所谓的多尺度视网膜增强算法(MSR, Multi-Scale Retinex),最为经典的就是 3 尺度的,大、中、小,既能实现图像动态范围的压缩,又能保持色感的一致性较好。同单尺度相比,该算法有在计算 Log[R(x,y)] 的值时步骤有所不同:
- 需要对原始图像进行每个尺度的高斯模糊,得到模糊后的图像 Li(x,y), 其中小标 i 表示尺度数。
- 对每个尺度下进行累加计算。
公式如下所示:
其中 n 是尺度的数量, 是高斯模糊系数的向量, 是与第 k 个尺度相关的权重,其中
MSRCR 算法
由于 R 是对数域的输出,要转换为数字图像,必须将他们量化为 [0,255] 的数字图像范畴,关于这个量化的算法,有这极为重要的意义,他的好坏直接决定了最终输出的图像的品质。目前,结合上述文章中提出的一些过程,有 4 种方式进行处理:
-
直接线性量化,即采用下式进行处理。
-
在经典的 MSRCR 文章《A Multiscale Retinex for Bridging the Gap Between Color Images and the Human Observation of Scenes》中提出的 Canonical Gain/set 算法。
其中 G 和 b 为经验参数。
-
种方式的处理类似于 Photoshop 中的自动色阶,他把数据按照一定的百分比去除最小和最大的部分,然后中间的部分重新线性量化到 0 和 255 之间。
在用第二种或第三种方式处理时,最好还需要有个 Color Restoration 的过程,因为如果直接对 MSR 处理的结果进行量化,得到的图像往往整体偏灰度,这是由于原始的彩色值经过 log 处理后的数据范围就比较小了,这样各通道之间的差异也很小,而之后的线性量化比 log 曲线要平滑很多,因此整体就丧失了彩色。论文中提出了修正方式如下:
对于一些原始图像 HUE 较为合理的图,如果用经典的 MSRCR 算法,会导致处理后的图容易偏色,上述论文提出了对图像的 Intensity 数据进行 Retinex 处理,然后再把数据根据原始的 RGB 的比例映射到每个通道,这样就能在保留原始颜色分布的基础上增强图像,文章中称其为 MSRCP。
参考文献
https://blog.csdn.net/lz0499/article/details/81154937
https://cloud.tencent.com/developer/article/1422364
https://www.cnblogs.com/Imageshop/archive/2013/04/17/3026881.html
[[CameraISPYUVCE]]
[[CameraISPYUVHueAndSaturation]]






