前言

光学系统大的分类：

  • 几何光学 -> 光线（像磁场线一样，其实不存在为了更好的研究其宏观特性而人为设计出来的）。
  • 物理光学 -> 光波 （分析光的波函数）。
  • 量子光学 -> 光子 （em...）。

折射系数 (index of refraction)

在几何光学的模型中，材料的光学性质是由材料的折射系数确定的，我们用字母 n 来代表折射系数。n 是一个关于波长 \(\lambda\)的函数，不同波长的 n 不一样，也就是色散 (dispersion)。

折射系数与光速的关系为：

\[ n = \frac{真空中光速}{介质中光速} = \frac{c}{v} \]

前提：

  • 介质是均匀的 (homogenous)，即 n 在介质任意一点都是一样的。
  • 介质是各向同性的 (isotropic)，即 n 在光传播的任何方向都是相同的。

因为 \(v = \frac{c}{n}\)，我们可以把光从 A 传播到 B 所需的时间写成：

\[ t_{AB} = \int_{A}^{B} \frac{ds}{v} = \frac{1}{c} \int_{A}^{B}n \cdot ds \]

我们可以把 \(\int n \cdot ds\) 称作光程长度 (optical path length), 如果我们有一个点光源（面积无限小的理想化光源），如果有一表面满足等光程长度（传播时间都相等），我们就把这一表面称作几何波前 (geometrical wavefront)。在一个 n 是恒定的介质里，如果满足刚刚说的等光程长度的条件，那么这个波前就是一个球形波前 (spherical wavefront)。

费马原理 (Fermat's Principle)

费马原理（Fermat's principle）最早由法国科学家皮埃尔·德·费马在 1662 年提出：光传播的路径是光程取极值的路径。这个极值可能是极大值、极小值或函数的拐点。 最初提出时，又名“最短时间原理”：光线传播的路径是需时最少的路径。 费马原理更正确的称谓应是“平稳时间原理”：光沿着所需时间为平稳的路径传播。平稳是数学上的微分概念，可以理解为一阶导数为零，它可以是极大值、极小值甚至是拐点。 费马原理是几何光学的基本定理。用微分或变分法可以从费马原理导出以下三个几何光学定律：

  • 光线在真空中的直线传播。
  • 光的反射定律 - 光线在界面上的反射， 入射角必须等于出射角。
  • 光的折射定律（斯涅尔定律）。

斯涅尔定律 (Snell's Law)

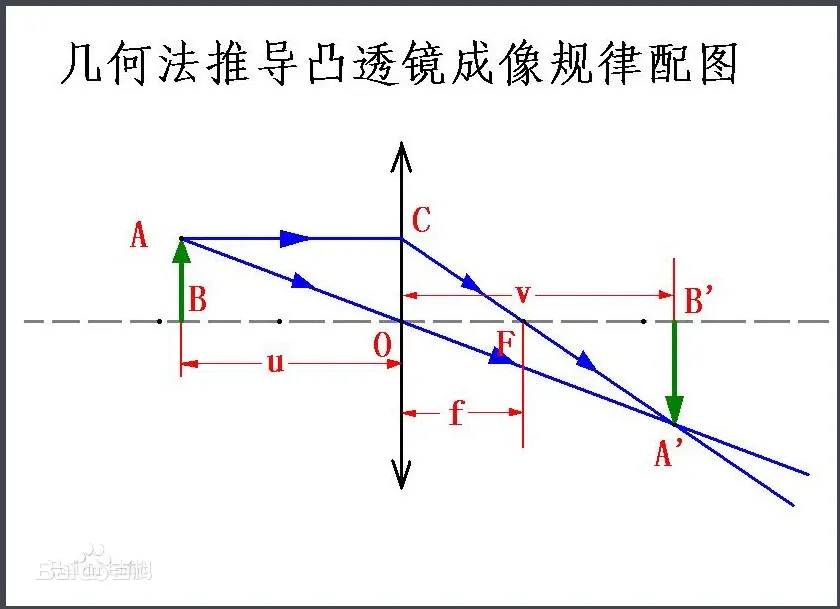
成像公式，即透镜成像公式、高斯成像公式，其形式为 \(\frac{1}{f} =\frac{1}{u} +\frac{1}{v}\)。其中 f 为焦距，凸正凹负；u 为物距；v 为像距，实正虚负。

衍射定律 TODO（待补充）

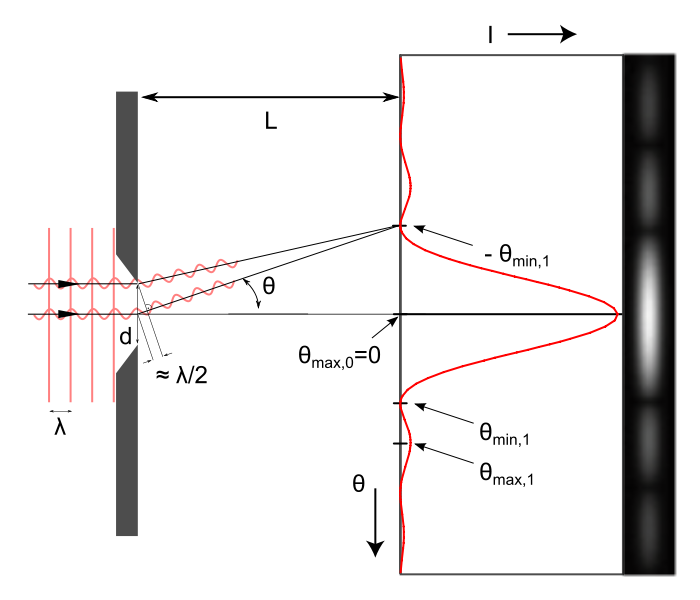
光在传播路径中，遇到不透明或透明的障碍物或者小孔（窄缝），绕过障碍物，产生偏离直线传播的现象称为光的衍射。衍射时产生的明暗条纹或光环，叫衍射图样。包括：单缝衍射、圆孔衍射、圆板衍射及泊松亮斑

理想光学系统与完美成像

理想光学系统

如果物空间中的一个物点 P 发出的发散球面波经过成像系统变换成一个汇聚球面波，球面波中心为 P‘，则此系统称为理想光学系统。

理想光学系统的物像关系应具备以下特性：

  • 点成点像：即对于物空间的每一点，在像空间必有一个点与之相对应，且只有一个点与之对应，这样的两个对应点称为物像空间的共轭点。
  • 线成线像：即对于物空间的每一条直线，在像空间必有一条直线与之相对应，且只有一条直线与之对应，这样的两条对应直线称为物像空间的共轭线。
  • 平面成平面像：即物空间的每一个平面，在像空间必有一个平面与之相对应，且只有一个平面与之对应，这样的两个对应平面称为物像空间的共轭面。

共线成像理论是理想光学系统的基础理论，它只是基本假设，实际中是不存在这样的理想光学系统的。显然，理想光学系统是实际光学系统的努力方向。

完美成像

高解析度 high resolution

系统可以分辨较高的空间频率，即光束在通过镜组时衍射现象尽可能的低。分辨解析极限即艾里斑直径要尽可能的小：

\[ d = 2.44 \cdot \lambda \cdot f \# \]

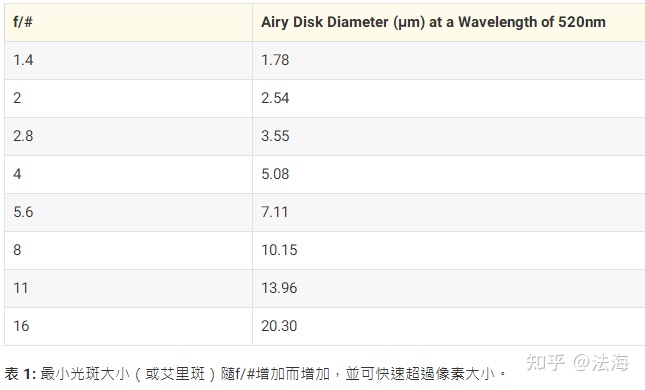
获得高解析度，方法有：

  • 降低 F-number 或提高 NA 值。
  • 使用波长更短的光源。

高对比度 high contrast

\[ C = \frac{I_{Max} - I_{Min}}{I_{Max} + I_{Min}} \]

色彩真实 true color

色彩真实是以人对色彩的感知作为参考基准的。现今对于颜色的描述，均使用数学方式定义色彩。色彩空间（英语：Color space）是对色彩的组织方式。借助色彩空间和针对物理设备的测试，可以得到色彩的固定模拟和数字表示。

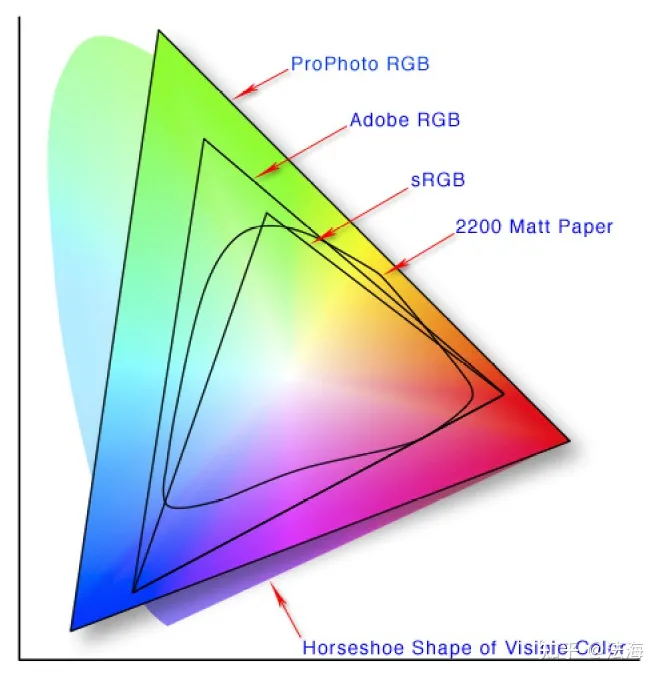
参考文献

https://zhuanlan.zhihu.com/p/357815034
https://zhuanlan.zhihu.com/p/534317287
https://zhuanlan.zhihu.com/p/339379757
https://www.wikiwand.com/zh-hans/%E6%96%AF%E6%B6%85%E5%B0%94%E5%AE%9A%E5%BE%8B
https://www.zhihu.com/people/EternaLSilence/posts