微积分（上）

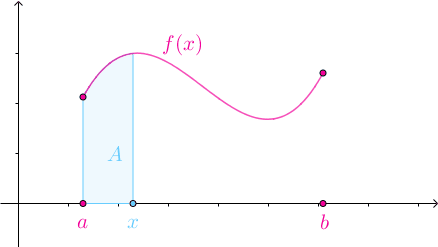
原图

极限

魏尔斯特拉斯的数列极限

设$x_n$为一数列，如果存在实数 L，对于任意给定的正实数$ϵ$（不论它多么小），总存在正整数 N，使得对所有的 n > N 时，有：

$$|x_n-L|<ϵ$$

那么就称 L 是数列$x_n$的极限，或者称数列$x_n$收敛于 L，记为：

$$\begin{array}{c}\underset{n\to \mathrm{\infty }}{lim}{x}_n=L\end{array}$$ 或 $$\begin{array}{c}{x}_n\to L(n\to \mathrm{\infty })\end{array}$$

一般函数的极限定义

设函数 f(x) 在$\mathring{U}(x_0)$上有定义。 如果存在常数 L，对任意给定的正数$ϵ$（不论它多么小），总存在正数$\delta$，使得当 x 满足不等式$0<|x-x_0|<\delta$时，对应的函数值 f(x) 都满足不等式：

$$|f(x)-L|<ϵ$$

那么常数 L 就叫做函数 f(x) 当$x\to x_0$的极限，记作：

$$\underset{x\to x_0}{lim}f(x)=L\text{ 或 }f(x)\to L(\text{ 当 }x\to x_0)$$

趋于$\pm \mathrm{\infty }$的函数极限定义

如果存在常数 L，对于任意给定的正数$ϵ$（不论它多么小），总存在着正数 X，使得当 x 满足不等式$|x|>X$时，对应的函数值 f(x) 满足不等式：

$$|f(x)-L|<ϵ$$

那么常数 L 就叫做函数 f(x) 当$x\to \pm \mathrm{\infty }$时的极限，记做：

$$\underset{x\to \pm \mathrm{\infty }}{lim}f(x)=L$$

无穷小与无穷大

对于数列$a=a_n$，如果满足：

$$\underset{n\to \mathrm{\infty }}{lim}{a}_n=0$$

则称数列 a 为$n\to \mathrm{\infty }$时的无穷小。

对于函数$f(x)$，如果满足：

$$limf(x)=0$$

则称函数$f(x)$为此自变量变化过程（指$x\to x_0,x\to +\mathrm{\infty }$等）的无穷小。

设函数$f(x)$在$x_0$的某一去心邻域内有定义，如果对于任意给定的正数 M（不论它多么大），总存在正数$\delta$，只要$x$适合不等式$0<|x-x_0|<\delta$，对应的函数值$f(x)$总满足不等式

$$f(x)>M$$

那么有：

$$\underset{x\to x_0}{lim}f(x)=+\mathrm{\infty }$$

这里有一个怪胎 0，0 到底是不是无穷小呢？在同济大学的高等数学教材里将 0 视为无穷小。因为它把常数 0 看作常值函数$f(x)\equiv 0$。但是我个人非常不喜欢把 0 视为无穷小，第一：无穷小不是一个实数，不然就可以通过除以二得到比他更接近 0 的数，而无穷小是最接近 0 的。第二：我们在微积分中分母经常出现无穷小，需要单独说明将 0 排除，很不爽。但是有很多时候可以将无穷小直接用 0 代替，使用上又很方便。

夹逼定理

有时候极限的求取没那么容易，这时有一种解决方案就是夹逼定理可以帮我们更好的找到数列或函数的极限：

如果满足下面两个条件：

$$\mathrm{\exists }\delta >0,\mathrm{\forall }x\in \stackrel{O}{U}(x_0,\delta ),g(x)\le f(x)\le h(x)$$

$$\underset{x\to x_0}{lim}g(x)=\underset{x\to x_0}{lim}h(x)=L$$

那么：

$$\underset{x\to x_0}{lim}f(x)=L$$

当然数列的夹逼定理定义也类似，这里不再列出。

连续和间断的定义

设函数$y=f(x)$在点$x_0$的某一邻域内有定义，如果： $$\underset{x\to x_0}{lim}f(x)=f\left(x_0\right)$$

那么就称函数$f(x)$在点$x_0$连续。

连续讨论的前提是$f(x)$在邻域上有定义，而间断讨论的前提是$f(x)$在去心邻域上有定义。在此前提下，如果函数有下列三种情况之一：

• 在$x=x_0$没有定义。
• 虽在$x=x_0$有定义，但$\underset{x\to x_0}{lim}f(x)$不存在。
• 虽在$x=x_0$有定义，且$\underset{x\to x_0}{lim}f(x)$存在，但$\underset{x\to x_0}{lim}f(x)\ne f(x_0)$。

那么函数$f(x)$在点$x_0$为不连续，而点$x_0$称为函数$f(x)$的不连续点或间断点。

所有的基本初等函数都是连续函数。基本初等函数进行有限次的四则运算和有限次的复合，得到的函数称为初等函数，初等函数也都是连续函数。

总结

在微积分中核心思想就是对自变量进行无线细分，以直代曲、无线逼近，而这些都设计无穷小量，为了对无穷小量进行定义，首先需要研究极限，无穷小量就是通过极限来定义的。极限的定义经历了柯西极限定义，直到魏尔斯特拉斯给出严格的数学定义，分为离散变量（数列）和连续变量（函数）的定义；有了极限就可以定义无穷小和无穷大。进而研究了无穷小和无穷大相关性质，最后给出研究微积分非常重要的条件连续的定义，这一切都离不开极限的定义，可以说极限的定义为微积分铺平了道路，后面的微积分你会发现无一不是极限。

微分

微分的定义

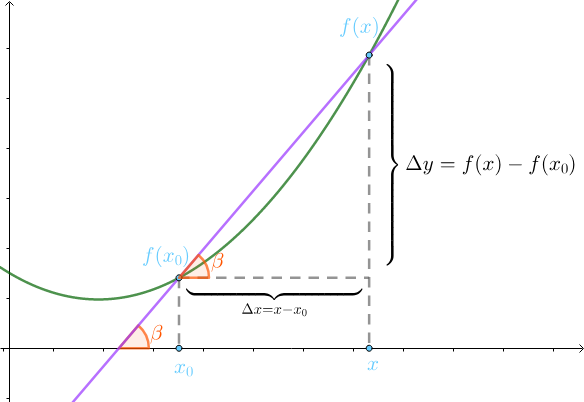
一条曲线上某点的割线，当另一个交点逐渐靠近这点时，取极限就是切线，即割线的极限是切线。由上图可知：

$$\mathrm{切}\mathrm{线}\mathrm{的}\mathrm{斜}\mathrm{率}=\underset{x\to x_0}{lim}\frac{f(x)-f\left(x_0\right)}{x-x_0}$$

这个极限就被称为导数：

设函数$y=f(x)$在点$x_0$的某个邻域内有定义，当自变量$x$在$x_0$处取得增量$\mathrm{\Delta }x$（点$x_0+\mathrm{\Delta }x$仍在该邻域内）时，相应的，因变量取得增量$\mathrm{\Delta }y=f(x_0+\mathrm{\Delta }x)-f(x_0)$。 如果$\mathrm{\Delta }y$与$\mathrm{\Delta }x$之比当$\mathrm{\Delta }x\to 0$时的极限存在，那么称函数$y=f(x)$在点$x_0$处可导，并称这个极限为函数$y=f(x)$在点$x_0$处的导数，记为$f^{\prime }(x_0)$，即：

$$f^{\prime }\left(x_0\right)=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f(x_0+\mathrm{\Delta }x)-f\left(x_0\right)}{\mathrm{\Delta }x}$$

有了导数$f^{\prime }(x_0)$之后，再知道切点$A=(x_0,f(x_0))$，就可以用直线的点斜式得到切线函数：

$$g(x)=f^{\prime }\left(x_0\right)(x-x_0)+f\left(x_0\right)$$

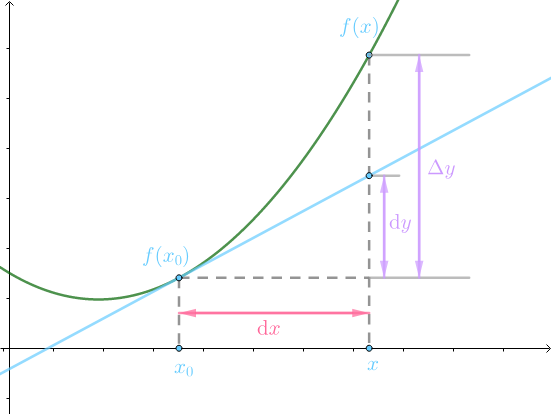
$\text{d}y$被称为线性增量，同理$\mathrm{\Delta }y$被称为曲线增量，定义了线性增量和曲线增量后，切线对曲线的近似用一个代数式就可以清楚表示：

$$\mathrm{\Delta }y-\mathrm{d}y=o(\mathrm{\Delta }x)$$

这个代数换个形式就是：

$$\underset{\mathrm{\Delta }x\to 0}{lim}[\mathrm{\Delta }y-\mathrm{d}y]=0$$

这个代数式的意思就是，随着$\mathrm{\Delta }x$缩小，$\text{d}y$和$\mathrm{\Delta }y$会无限接近：

到这里我们终于可以给出微分的定义：

设函数$y=f(x)$在某区间内有定义，$x_0$及$x_0+\mathrm{\Delta }x$在此区间内，如果函数增量：

$$\mathrm{\Delta }y=f(x_0+\mathrm{\Delta }x)-f\left(x_0\right)$$

可表示为：

$$\mathrm{\Delta }y=A\mathrm{\Delta }x+o(\mathrm{\Delta }x)$$

其中$A$是不依赖于$\mathrm{\Delta }x$的常数，那么称函数$y=f(x)$在点$x_0$是可微的，而$A\mathrm{\Delta }x$叫作函数$y=f(x)$在点$x_0$相应于自变量增量$\mathrm{\Delta }x$的微分，记作$\text{d}y$，即：

$$\mathrm{d}y=A\mathrm{\Delta }x$$

导函数

设函数$y=f(x)$在开区间$I$内的每点处都可导，则称函数$y=f(x)$在开区间$I$内可导。 这时，对于任意$x\in I$，都对应着$f(x)$的一个确定的导数值，这就构成了新的函数，这个函数叫作$y=f(x)$的导函数，记作$y^{\prime }$或$f^{\prime }(x)、\frac{\text{d}y}{\text{d}x}、\frac{\text{d}f(x)}{\text{d}x}$，定义式为：

$$y^{\prime }=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}$$

导数是某一点切线的斜率，导函数就是区间内所有点的切线的斜率构成的函数：

有了导函数后，就可以得到函数的微分：

$$\mathrm{d}y=f^{\prime }(x)\mathrm{d}x$$

所以函数的微分实际上是一个二元函数，注意区分$x$和$dx$，或许写成这样更明确：

$$\mathrm{d}y=f^{\prime }(x)\mathrm{d}x⟹h(x,\mathrm{d}x)=f^{\prime }(x)\mathrm{d}x$$

求导以及导数的运算法则

微分是导数和$dx$的乘积，因此导数的求取及其运算法则就相当重要，关于初等函数求导法则这里不做详述，会查表即可。下面列出导数的运算法则：

• 和差： $$[u(x)\pm v(x){]}^{\prime }=u^{\prime }(x)\pm v^{\prime }(x)$$

• 积： $$[u(x)v(x){]}^{\prime }=u^{\prime }(x)v(x)+u(x)v^{\prime }(x)$$

• 商： $${\left[\frac{u(x)}{v(x)}\right]}^{\prime }=\frac{u^{\prime }(x)v(x)-u(x)v^{\prime }(x)}{v^2(x)}(v(x)\ne 0)$$

• 复合函数求导（链式法则）： 如果$u=g(x)$在点$a$可导，而$y=f(u)$在点$b=g(a)$可导，那么复合函 数$y=f[g(x)]$在点$a$可导，且其导数为：

  $$\frac{\mathrm{d}y}{\mathrm{d}x}=f^{\prime }(b)g^{\prime }(a)$$

  或

  $$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}u}\cdot \frac{\mathrm{d}u}{\mathrm{d}x}$$

• 反函数求导： 如果函数$y=f(x)$在区间$I$内单调、可导且$f^{\prime }(x)\ne 0$，那么它的反 函数$f^{-1}(x)$在区间$\{y=f(x),x\in I\}$内也可导。且：

  $${[f^{-1}(y)]}^{\prime }=\frac{1}{f^{\prime }(x)}$$

• 隐函数求导：

  • 第一步，对方程两边求关于 $x$的微分，这样就可以得到一个关于 $y^{\prime }$ 的 方程；
  • 第二步，在微分后的方程中求解$y^{\prime }$既可。

• 参数方程求导： 对于参数方程：

  $$\{\begin{array}{l}x=x(t)\\ y=y(t)\end{array}$$

  其中$x(t)$和$y(t)$可导，且$x(t)$单调， $x^{\prime }(t)\ne 0$，则：

  $$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{y^{\prime }(t)}{x^{\prime }(t)}$$

关于高阶导数定义和运算这里不再列出。

微分相关性质

前面我们已经提到微分以及导数的定义以及如何求取，下面就是关于微分相关性质的研究了，其中最重要的就是几个中值定理。

• 费马引理： $$\begin{array}{c}f(a)\text{ 为极值点 }\\ x=a\text{ 点可导 }\end{array}\}⟹f^{\prime }(a)=0$$

  这就是费马引理。

  其中极值点的定义如下：

  已知函数$y=f(x)$，则：

  • $f(a)$是极大值，当且仅当$\mathrm{\exists }\delta >0，\mathrm{\forall }x\in \mathring{U}(a,\delta )$，有$f(x)<f(a)$
  • $f(a)$是极小值，当且仅当$\mathrm{\exists }\delta >0，\mathrm{\forall }x\in \mathring{U}(a,\delta )$，有$f(x)>f(a)$

• 罗尔中值定理： 设函数满足以下三个条件：

  • $f(x)$在闭区间$[a,b]$上连续
  • $f(x)$在开区间$(a,b)$上可导
  • $f(a)=f(b)$ 则存在$\xi \in (a,b)$，使得$f^{\prime }(\xi )=0$

• 微分中值定理： 设函数满足以下两个条件：

  • $f(x)$在闭区间$[a,b]$上连续
  • $f(x)$在开区间$(a,b)$上可导

  则存在$\xi \in (a,b)$，使得$f^{\prime }(\xi )=\frac{f(b)-f(a)}{b-a}$

  这个定理的几何意义就是，至少存在一点的切线与端点的连线平行；物理意义 是，至少存在一点的速度与平均速度相等：

  

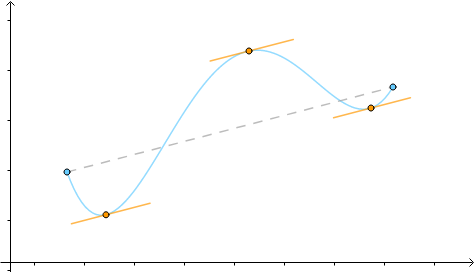
• 柯西中值定理： 设函数$f(x),g(x)$满足以下条件：

  • $f(x),g(x)$在闭区间$[a,b]$上连续
  • $f(x),g(x)$在开区间$(a,b)$上可导
  • $\mathrm{\forall }x\in (a,b)$有：$g^{\prime }(x)\ne 0$

  则存在$\xi \in (a,b)$，使等式：

  $$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime }(\xi )}{g^{\prime }(\xi )}$$

  成立。

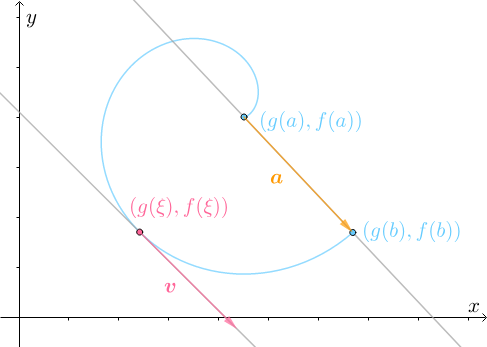
  直观理解：对于参数方程 $$\{\begin{array}{l}x=g(t)\\ y=f(t)\end{array}$$ 如下： 此时，$\mathit{a}$所在直线的斜率： $$\frac{f(b)-f(a)}{g(b)-g(a)}$$ 以及$\mathit{v}$所在直线的斜率（根据参数方程的求导法则）： $$\frac{f^{\prime }(\xi )}{g^{\prime }(\xi )}$$ 必然相等： $$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime }(\xi )}{g^{\prime }(\xi )}$$

• 洛必达法则： $\frac{0}{0}$型：设：

  • $\underset{x\to a}{lim}f(x)=\underset{x\to a}{lim}g(x)=0$
  • 某$\mathring{U}(a)$内，$f^{\prime }(x)$及$g^{\prime }(x)$都存在，且$g^{\prime }(x)\ne 0$
  • ${\displaystyle \underset{x\to a}{lim}\frac{f^{\prime }(x)}{g^{\prime }(x)}}$存在（或为无穷大） 则： $$\underset{x\to a}{lim}\frac{f(x)}{g(x)}=\underset{x\to a}{lim}\frac{f^{\prime }(x)}{g^{\prime }(x)}$$

  $\frac{\mathrm{\infty }}{\mathrm{\infty }}$型：设：

  • $\underset{x\to a}{lim}f(x)=\pm \mathrm{\infty }，\underset{x\to a}{lim}g(x)=\pm \mathrm{\infty }$
  • 某$\mathring{U}(a)$内，$f^{\prime }(x)$及$g^{\prime }(x)$都存在，且$g^{\prime }(x)\ne 0$
  • ${\displaystyle \underset{x\to a}{lim}\frac{f^{\prime }(x)}{g^{\prime }(x)}}$存在（或为无穷大） 则： $$\underset{x\to a}{lim}\frac{f(x)}{g(x)}=\underset{x\to a}{lim}\frac{f^{\prime }(x)}{g^{\prime }(x)}$$

• 牛顿插值法： 关于牛顿插值法的思想请参考 https://www.zhihu.com/question/22320408 马同学的回答，这里不再列出。

• 泰勒公式： 设$f(x)$在$x=x_0$处$k$阶可导，则对于任何在 0 到$k$之间的整数$n$，可以生成 n 阶泰勒多项式： $$\begin{array}{rl}{p}_n(x)=& f\left(x_0\right)+f^{\prime }\left(x_0\right)(x-x_0)+\frac{f^{\prime \prime }\left(x_0\right)}{2!}{(x-x_0)}^2\\ & +\cdots +\frac{f^{(n)}\left(x_0\right)}{n!}{(x-x_0)}^n\end{array}$$ 特别的，如果在$x=0$处生成的泰勒多项式，也称为 n 阶麦克劳林多项式： $$p_n(x)=f(0)+f^{\prime }(0)x+\frac{f^{″}(0)}{2!}{x}^2+\cdots +\frac{f^{(n)}(0)}{n!}{x}^n$$ 泰勒公式是牛顿插值法的进阶。

积分

定积分

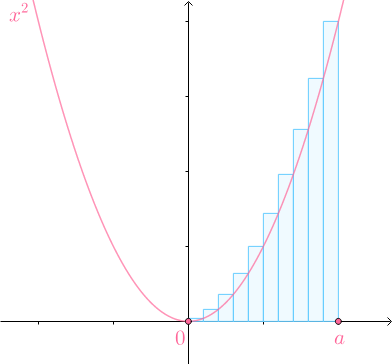
直观理解积分就是，以每个小方形面积取代曲边形面积，当 x 取极限时每个小长方形的面积就是微分，而所有的长方形面积之和就是积分。 下面是定积分的定义：

设函数$f(x)$在$[a,b]$上有定义，对于$[a,b]$上的任意划分$P$，${\xi }_k$为子区间$[x_{k-1},x_k]$上任意选取的数，子区间$[x_{k-1},x_k]$的长度为$\mathrm{\Delta }{x}_k$，记：

$$\lambda =max\{\mathrm{\Delta }{x}_1,\mathrm{\Delta }{x}_2,...,\mathrm{\Delta }{x}_n\}$$

如果当$\lambda \to 0$时

$$S=\sum _{i=1}^{n}f\left({\xi }_i\right)\mathrm{\Delta }{x}_i$$

的极限总是存在，且与闭区间$[a,b]$的分法及点${\xi }_i$的取法无关，那么称这个极限 I 为函数$f(x)$在区间$[a,b]$上的定积分，记做${\int }_a^{b}f(x)dx,$即：

$${\int }_a^{b}f(x)\mathrm{d}x=I=\underset{\lambda \to 0}{lim}\sum _{i=1}^{n}f\left({\xi }_i\right)\mathrm{\Delta }{x}_i$$

其中 a 为积分下限，b 为积分上限，$I$为$f(x)$在$[a,b]$上的定积分，x 为积分变量。

定积分的性质

• 可积条件：

  • 如果$f(x)$在$[a,b]$上连续，则$f(x)$在$[a,b]$上可积
  • 如果$f(x)$在$[a,b]$上有界，且只有有限个间断点，则$f(x)$在$[a,b]$上可积

• 齐次性： $${\int }_a^{b}cf(x)\text{d}x=c{\int }_a^{b}f(x)\text{d}x,c\in \mathbb{R}$$

• 可加性： $${\int }_a^b[f(x)+g(x)]\text{d}x={\int }_a^{b}f(x)\text{d}x+{\int }_a^{b}g(x)\text{d}x$$

• 积分中值定理： 如果函数$f(x)$在积分区间$[a,b]$连续，那么在$[a,b]$上至少存在一点$\xi$，使下式成立： $${\int }_a^{b}f(x)dx=f(\xi )(b-a),\xi \in [a,b]$$

微积分基本定理

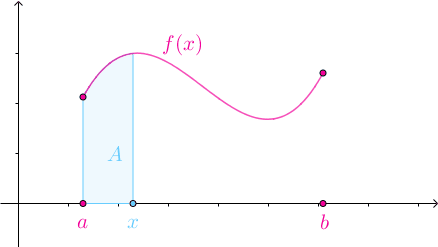
b 端点变成一个变量，定积分就变成关于该变量的积分上限函数，如下：

$$A(x)={\int }_a^{x}f(x)\text{d}x$$

因为$x$又表示积分函数，又表示积分变量，为了避免混淆，所以一般如下表示：

$$A(x)={\int }_a^{x}f(t)\text{d}t$$

牛顿-莱布尼兹公式 $f(x)$在$[a,b]$上连续，$F(x)$是$f(x)$的一个原函数，那么：

$${\int }_a^{b}f(x)\text{d}x=F(b)-F(a)$$

也可以记作：

$${\int }_a^{b}f(x)\text{d}x=[F(x){]}_a^b$$

可以这样理解，$F(x)$对 x 求导代表的是在 x 点的变化率，而对于$f(x)$在 x 点的变化量正好就是$F(x)$在 x 点的变化率在 x 取极限的情况下。

不定积分

如果$F(x)$是$f(x)$在区间$I$上的一个原函数，那么$F(x)+C$就是$f(x)$的不定积分，即：

$$\int f(x)\text{d}x=F(x)+C,C\in \mathbb{R}$$

并且不定积分$\int f(x)dx$表示了$f(x)$的所有原函数。

积分表

$$\overline{)\begin{array}{c}\\ \int k\text{d}x=kx+C& \int \cos x\text{d}x=\sin x+C\\ \int x^n\text{d}x=\frac{x^{n+1}}{n+1}+C,(n\ne -1)& \int \sin x\text{d}x=-\cos x+C\\ \int \frac{1}{x}\text{d}x=\ln |x|+C& \int {\sec }^{2}x\text{d}x=\tan x+C\\ \int \frac{1}{\sqrt{a^2-x^2}}\text{d}x=\arcsin \frac{x}{a}+C& \int {\csc }^{2}x\text{d}x=-\cot x+C\\ \int e^x\text{d}x=e^x+C& \int \sec x\tan x\text{d}x=\sec x+C\\ \int a^x\text{d}x=\frac{a^x}{\ln a}+C& \int \csc x\cot x\text{d}x=-\csc x+C\\ \int \frac{1}{a^2+x^2}\text{d}x=\frac{1}{a}\arctan \frac{x}{a}+C& \int \tan x\text{d}x=\ln |\sec x|+C\\ \end{array}}$$

积分方法

• 线性性质： 设函数$f(x)$及$g(x)$的原函数存在，则（可加性）：

  $$\int [f(x)+g(x)]dx=\int f(x)dx+\int g(x)dx(1)$$

  $k$为非零常数（齐次性）：

  $$\int kf(x)dx=k\int f(x)dx(2)$$

• 第一类换元法： 设$f(u)$具有原函数$F(u)$，$u=u(x)$可导，则有换元公式：

  $$\int f[\underset{u}{\underbrace{u(x)}}]\underset{\text{d}u}{\underbrace{u^{\prime }(x)\text{d}x}}=\int f(u)\text{d}u=F(u)+C$$

• 第二类换元法： 设$x=x(t)$是单调的可导函数，且$x^{\prime }(t)\ne 0$，则$t$可以用$x$来表示，即有反函数： $$t=t(x)$$ 如果有： $$\int f(x)\text{d}x\stackrel{\mathrm{换}\mathrm{元}x=x(t)}{\to }\int f[x(t)]x^{\prime }(t)\text{d}t=F(t)+C$$ 则： $$\int f(x)\text{d}x=F(t(x))+C$$

• 定积分的换元： 假设函数$f(x)$在区间$[a,b]$上连续，函数$x=g(t)$满足条件：

  • $g(\alpha )=a,g(\beta )=b$
  • $g(t)$在$[\alpha ,\beta ]$（或$[\beta ,\alpha ]$) 上具有连续导数，且其值域$R_g=[a,b]$，则有： $${\int }_a^{b}f(x)dx={\int }_{\alpha }^{\beta }f[g(t)]g^{\prime }(t)dt$$

  定积分的换元和不定积分的换元的不同之处在于：

  • 定积分换元时，需要变量与积分限同时换
  • 在定积分换元后，利用牛顿-莱布尼茨公式可以直接计算出结果，不需要回代

• 分部积分法： $f(x),g(x)$皆为可导函数，有： $$\int f(x)g^{\prime }(x)dx=f(x)g(x)-\int g(x)f^{\prime }(x)dx$$ 或设$u=f(x),v=g(x)$，上式可以写作： $$\int udv=uv-\int vdu$$

微分方程

方程简单而言就是含有未知量的等式；特别地，含有未知函数及其导函数的方程称为微分方程：

$$\overline{)\begin{array}{ccc}& \mathrm{未}\mathrm{知}\mathrm{数}、quad& \mathrm{例}\mathrm{子}、quad\\ \mathrm{方}\mathrm{程}& x& 2x+1=3\\ \mathrm{微}\mathrm{分}\mathrm{方}\mathrm{程}& y& \frac{\mathrm{d}y}{\mathrm{d}x}+xy=2x\end{array}}$$

可分离变量的微分方程

如果一阶微分方程可以写成： $$g(y)\mathrm{d}y=f(x)\mathrm{d}x$$ 的形式，这就是可分离变量的微分方程。

可以直接对两边求不定积分，比较简单。

如果一阶微分方程可以写成： $$\frac{\mathrm{d}y}{\mathrm{d}x}=\phi \left(\frac{y}{x}\right)$$

的形式，那么称此方程为齐次方程。这个方程是可以通过 换元变换为可分离变量的微分方程的。

线形微分方程

定义

$$\mathcal{L}=a_0+a_{1}D+a_2{D}^2+a_3{D}^3+\cdots +a_n{D}^n$$ 也是矩阵，也是线性函数，多项式组合、mathcal{L}称为微分算子。

对于微分算子：

$$\mathcal{L}=a_0+a_{1}D+a_2{D}^2+a_3{D}^3+\cdots +a_n{D}^n$$

下式：

$$\mathcal{L}(y)=f(x)$$

称为线性微分方程。如果$f(x)$： - 等于 0：齐次线性微分方程。 - 不等于 0：非齐次线性微分方程。

如果系数$a_0,a_1,\cdots ,a_n：$

• 是常数：常系数线性微分方程。
• 是函数：变系数线性微分方程。

线性微分方程解的结构

如果${\mathit{p}}_{\mathbf{1}}、{\mathit{p}}_{\mathbf{2}}$是齐次线性方程组： $$A\mathit{x}=\mathbf{0}$$

的解，那么它们的线性组合：

$${\mathit{p}}_{\mathbf{3}}=C_1{\mathit{p}}_{\mathbf{1}}+C_2{\mathit{p}}_{\mathbf{2}}(C_1,C_2\in \mathbb{R})$$

也是此线性方程组的解。

如果${\mathit{p}}_{\mathbf{1}},{\mathit{p}}_{\mathbf{2}},\cdots ,{\mathit{p}}_{\mathit{n}}$是 n 维齐次线性方程组：

$$A\mathit{x}=\mathbf{0}$$

的解，并且它们线性无关，那么线性组合：

$$\mathit{p}=C_1{\mathit{p}}_{\mathbf{1}}+C_2{\mathit{p}}_{\mathbf{2}}+\cdots +C_n{\mathit{p}}_{\mathit{n}}(C_1,C_2,\cdots ,C_n\in \mathbb{R})$$

是此方程组的通解。

如果： $$\mathit{p}=C_1{\mathit{p}}_{\mathbf{1}}+C_2{\mathit{p}}_{\mathbf{2}}+\cdots +C_n{\mathit{p}}_{\mathit{n}}(C_1,C_2,\cdots ,C_n\in \mathbb{R})$$

是齐次线性方程组：

$$A\mathit{x}=\mathbf{0}$$

的通解。${\mathit{p}}^{\mathbf{\ast }}$是非齐次线性方程组：

$$A\mathit{x}=\mathit{b}$$

的一个解，也称为特解，那么：

$$\mathit{p}+{\mathit{p}}^{\mathbf{\ast }}$$

是非齐次线性方程组的所有解。

常系数线性微分方程

微分算子$\mathcal{L}$是 D 的多项式组合： $$\mathcal{L}=a_0+a_{1}D+a_2{D}^2+a_3{D}^3+\cdots +a_n{D}^n$$ 如果系数$a_0,a_1,\cdots ,a_n$是常数，那么： $$\mathcal{L}(y)=f(x)$$

就是常系数微分方程。根据线性微分方程解的结构，我们可以来看齐次解。 某二阶常系数齐次线性微分方程： $$y^{″}+p{y}^{\prime }+qy=0$$

其中$p、q$是常数。大神欧拉发现不论$p、q$是什么，通解都具有以下形式：

$$Y=C_1{e}^{r_{1}x}+C_2{e}^{r_{2}x}$$

$r_1、r_2$是复数。那么可以合理假设$y=e^{rx}$，得到：

$$y^{\prime }=r{e}^{rx},y^{″}=r^2{e}^{rx}$$

回代到微分方程中，得到：

$$(r^2+pr+q)e^{rx}=0$$

那么上面等式要成立，只能是：

$$r^2+pr+q=0$$

这是一个一元二次方程，也被称为此微分方程的特征方程。

可以用公式：

$$r_{1,2}=\frac{-p\pm \sqrt{p^2-4q}}{2}$$

求出 r_1、r_2

变系数线性微分方程

• 一阶变系数线性微分方程： 一阶变系数线性微分方程经过变形之后都可以写成如下的形式： $$\frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x)$$ 可以先写为齐次方程，然后对两边进行积分求解。然后再求解非齐次方程的解。

• 伯努利微分方程： $$\frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x)y^n(n\ne 0,1)$$ 叫做伯努利微分方程。 可以变成了一阶变系数线性微分方程来求解。

• 欧拉方程： $$x^n{y}^{(n)}+p_1{x}^{n-1}{y}^{(n-1)}+\cdots +p_{n-1}x{y}^{\prime }+p_{n}y=f(x)$$ 称为欧拉方程。 欧拉方程也可以转为常系数线性微分方程。

这里没有将具体的解法列出来，而只是以提纲的方式将概念理出来，具体的解法可以参考相关参考书。

参考文献

《马同学的单变量微积分课程》
感兴趣的可以购买他的课程，写的很好（强烈推荐）！！！