光速测量史

罗默测定光速（1676年）

太阳（点A）照射于木星（点B）会产生阴影（范围从木卫一轨道的点C至点D）。从地球观察，当木卫一蚀发生之时（点C），木卫一会突然消失，运行进入木星阴影，称这现象为“消踪”；当木卫一蚀结束之时（点D），木卫一会突然出现，运行离开木星阴影，称这现象为“现踪”。

地球的公转轨道包含了点E、F、G、H、L、K。在任意一次木卫一蚀里，消踪与现踪不能够从地球都观察得到，因为其中一种现象必会被木星掩蔽。在冲日点（点H，地球在太阳与木星连线之间），消踪与现踪都会被木星掩蔽。在地球位置点L、K都可以观察到木卫一现踪（点D）。由于点L比点K接近点D，光波需要更多传播时间才能抵达点K。类似地，在地球位置点F、G都可以观察到木卫一消踪（点C）。由于点G比点F接近点C，光波需要较少传播时间才能抵达点G。

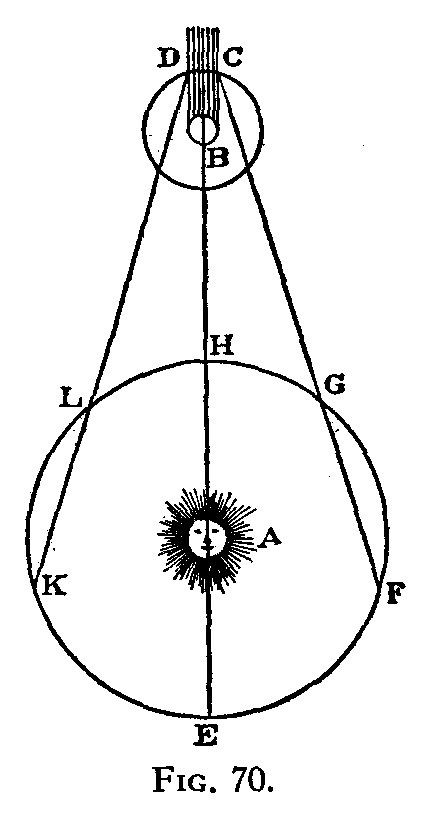
由于光线从D点到L和到K的距离不同导致在这两个点观察到的木卫一蚀时间上存在差异，罗默就利用这个时间差以及L与K之间的距离估算出了光速，当然罗默测的光速比实际慢了26%，这是由于当时对木星的轨道根数的错误造成的误差导致的。天文学家通过对天体的观察就推算出了光速，确实非常了不起。

斐索测定光速（1849年）

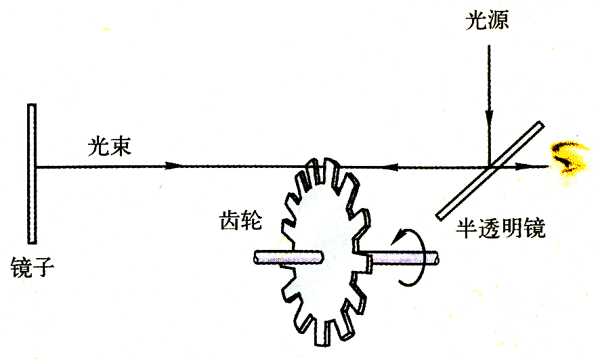
当光源经过半透镜的反射（也会存在投射射向下方）会通过齿轮的间隙穿过（齿轮的位置满足一定的条件）然后到达对面的镜子后反射回来，如果齿轮不转动那么光线会经过原缝隙返回到半透明镜，经过透射（当然同时也存在反射，不过此时不关心反射）后被观察到。如果齿轮开始转动，如果速度慢那么光线依然会经过原缝隙返回，直到速度达到某个临界值后光线返回会打在齿轮上而不能被穿过齿轮到达半透明镜进入人眼，那么就可以通过齿轮转过一个齿所需的时间以及齿轮与镜子之间距离的二倍计算出光速。实际上实验并没那么容易做因为，必须要求每次光都通过齿轮间隙射向镜子，而每次镜子反射过来的光又恰好打在齿上才可以，这个是需要大量的齿轮以及齿轮与镜子之间距离的调整才能实验成功的。不过最终还是被斐索给做出来了。斐索测得的光速比后来被公认的光速高了约5%。

这里隐含了一个假设就是光速经过镜子的反射后光速不变才行

傅科测定光速（1850年）

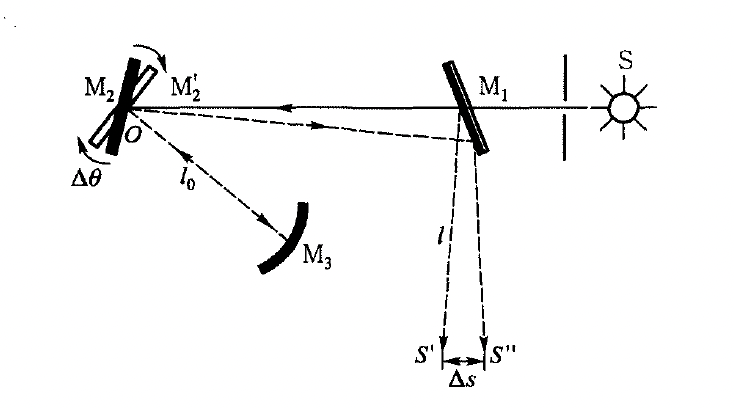
从光源S所发出的光通过半镀银的镜面M1后，射在绕0轴旋转的平面反射镜M2上，0轴与图面垂直．光从M2反射而会聚到凹面反射镜M3上，M3 的曲率中心恰在0轴上，所以光线由M3 对称地反射，若平面反射镜M2 的位置未变，则光仍沿原光路射回，并在s‘ 点产生光源的像．而如果平面反射镜M2因旋转而镜面发生改变，则光射回时将与原光路略有偏移，像s’ 的位置将改变到s”，相对于可视M2 为不转时的位置移动了△s的距离.那么根据以上数据也可以计算出光速

$c = \frac{4 ω l l_{0}}{Δ s}$

其中

$Δ s = 2 Δ θ \cdot l$

$Δ θ$ 为旋转镜M2转动的角度。这个实验存在一个难点就是测 $Δ θ$ 不那么容易。

迈克耳孙—光速测定的集大成者（1926年）

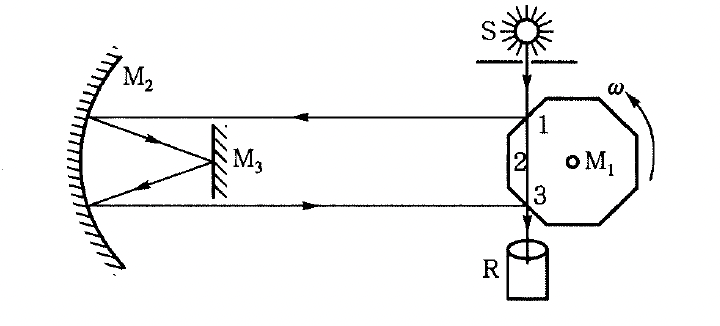
光源s发出的光，经过狭缝射到正八角棱镜M1的面1上，反射后射到放置在另一个山峰的凹面镜M2上，又反射到平面镜M3 上，经过M3，反射后，再由M2 反射回第一个M1．如果正八角棱镜M1 静止不动，反射回来的光就射到正八角棱镜M1的另一个面3上，经过3反射后，通过望远镜R进入观察者的眼中，看到光源s的像．如果使正八角棱镜转动，那么光反射回来时，正八角棱镜的面3已经偏离了原来的取向，经过3反射后的光不再进入望远镜中，观察者就观察不到光源s的像了．适当调节正八角棱镜的转速，使发射回来的光到达正八角棱镜时，正八角棱镜恰好转过一面，即面2刚好转到面3原来的位置，经面2反射后的光进入望远镜中，就可以重新看到s的像．根据正八角棱镜转过1／8转所用的时间和M1 M2间的距离，就可以算出光在空气里的速度．

1929年以后，对光速的测量进入了一个新阶段．新的实验方法和新的实验技术不断涌现，使得测量精度不断提高，最终使光速成为物理学上的一个定义值．

所有光速测量都是测量的往返路程，其前提假设是光速反射后速度不变，目前为止单向光速的测量都未成功。

电磁波的速度

麦克斯韦预言了电磁波的存在而赫兹证明了电磁波的存在（实验科学），而可见光其实就是电磁波中很小的一段。在电动力学里，根据马克士威方程组，随著时间变化的电场产生了磁场，反之亦然。因此，一个振荡中的电场会产生振荡的磁场，而一个振荡中的磁场又会产生振荡的电场，这样子，这些连续不断同相振荡的电场和磁场共同地形成了电磁波。因此光速跟电磁波的速度本质是一样的，有了电磁波就可以研究电磁波的速度与频率和波长之间的关系，因此有了如下如此美妙的公式：

$v = f λ f = \frac{E}{h}$

其中， v是波速（在真空里是光速；在其它介质里，小于光速）， f是频率，λ是波长,E是光子能量，h是普朗克常数。其中光在真空中的速度为常数c，即光在真空中速度是不变的。

光速不变论

光速不变原理指出，在所有惯性参考系中，光速在真空中的速度都是一个常数，约为299,792,458米/秒，与光源和观察者的运动状态无关。

其支持理论有：

迈克尔逊-莫雷实验

在上一篇光的本性之争一文中有介绍该实验，原本是用来证明以太不存在的，但其实也证明了光在沿各个不同的方向上传播速度是一样的。此实验不能证明光速不变只能证明光在不同方向上传播速度一样。

光谱线的多普勒效应

根据多普勒效应，当光源向观察者靠近时，光谱线向蓝端偏移；远离时则向红端偏移。通过对不同速度的光源进行观测，发现光速保持不变，与光源的运动状态无关，这与光速不变原理相符。多普勒效应是一个很好的证明例子，当光源向你移动时波长变短，发生蓝移现象，当光源远离你时光线发生红移现象波长变长。但是实验发现不同波长的电磁波传播速度一样，也就是给定光源一个速度后并不是光速发生了变化（光速c并没有叠加上光源的速度）而是频率和波长发生了变化。

雷达回波延迟测量

通过向行星或人造卫星发射雷达信号并测量回波的延迟时间，可以精确测量地月距离或其他天体的距离。这些测量结果表明，光速在不同方向上是相同的，与地球的运动状态无关，支持了光速不变原理。

Q：当波从一个介质传播至另一个介质时，波速会改变，但是频率不变。也就是说光速在不同介质中传播速度不同，而这与光速不变论是否相悖？

光速不变论指的是无论在何种惯性参照系中观察，光在真空中的传播速度相对于该观测者都是同一个常数，不随光源和观测者所在参考系的相对运动而改变。而光速在不同介质中的速度不同是因为光与介质中的原子和分子相互作用，导致其传播速度减慢。这种现象可以用折射率来描述，折射率是介质中光速与真空中光速的比值，两者说明的根本不是一个问题。

伽利略的相对性原理

伽利略在他关于落体的论述中首次提出了相对性原理。他指出，所有的惯性参考系（即匀速直线运动的参考系）都是等价的，没有哪一个参考系比其他参考系更特殊。这意味着在一个惯性参考系中进行的物理实验的结果，在另一个惯性参考系中也会得出相同的结果。

狭义相对论

狭义相对论基于两个基本假设：

相对性原理：物理定律在所有惯性参考系中都是相同的，即不存在一个特殊的惯性参考系。
光速不变原理：在真空中的光速在所有惯性参考系中都是相同的，与光源和观察者的运动状态无关。

如果光速不变论和相对性原理都是对的，那么就只能推翻牛顿建立的绝对时空观。当光源以一定的速度运动时光速保持不变，根据v=d/t，只能是d距离与时间t保持相同的比例。那么空间和时间就会是一体的。由三维空间变为四维空间一体。

基于这两个基本原理，狭义相对论还引入了以下几个重要概念：

相对论质量当物体的速度 (v) 接近光速 (c) 时，相对论质量 (m) 会变得非常大。在极端情况下，当 (v) 接近 (c) 时，相对论质量趋近于无穷大。这意味着，需要无限大的力才能将物体加速到光速。这也是为什么狭义相对论认为光速是物体所能达到的最大速度。

$m = \frac{m_{0}}{\sqrt{1 - (\frac{v}{c})^{2}}}$

相对论质量的概念在粒子加速器实验中得到了验证。在高能物理实验中，粒子被加速到接近光速，其质量的增加被精确测量。例如，电子在加速器中被加速到接近光速时，其惯性和质量的增加与相对论质量的预测一致。
时间膨胀（Time Dilation）当物体以接近光速运动时，其时间流逝会相对于静止观察者变慢。这种现象被称为时间膨胀。时间膨胀效应在高速粒子（如μ子）的衰变和高能物理实验中得到了验证。

$t = \frac{t_{0}}{\sqrt{1 - (\frac{v}{c})^{2}}}$

在1971年进行的维伯伦实验中，科学家们将铯原子钟放置在飞机上，分别沿着东行和西行的方向飞行，并与地面的原子钟进行比较。根据狭义相对论，飞机上的原子钟应该显示出时间膨胀效应，因为飞机相对于地面以高速运动。实验结果与理论预测相符，证明了时间膨胀现象的存在。

现代高精度原子钟的发展使得时间膨胀效应可以被直接测量。例如，美国国家标准与技术研究所（NIST）的实验中，将高精度铯原子钟放置在不同高度的位置，通过比较它们的时间差来验证广义相对论的时间膨胀效应。实验结果表明，由于重力势能的不同，高处的原子钟时间流逝得更快，符合广义相对论的预测。
长度收缩（Length Contraction）当物体以接近光速运动时，其沿运动方向的长度会相对于静止观察者缩短。这种现象被称为长度收缩。长度收缩是时间膨胀的互补效应，两者共同体现了相对论的时空观。

$L = L_{0} \sqrt{1 - (\frac{v}{c})^{2}}$

在某些双星系统中，一个恒星的运动速度可以达到接近光速。根据狭义相对论，这些高速运动的恒星在运动方向上的长度会收缩，这可能导致其引力场和光谱线的变化。天文学家通过观测这些系统的引力效应和光谱线，可以验证相对论的长度收缩预言。

在高能物理实验中，如大型强子对撞机（LHC），粒子被加速到极高的能量和速度。在与这些粒子相互作用的实验中，粒子的长度收缩效应会影响实验结果，如粒子的相互作用截面和散射角。通过精确测量这些结果并与相对论理论预测进行比较，科学家可以验证长度收缩的存在。
质能等价（Mass-Energy Equivalence）狭义相对论的一个重要结论是质能等价原理，即质量和能量可以互相转换。这个原理用著名的质能方程 (E = mc^2) 表示，其中 (E) 是能量，(m) 是质量，(c) 是光速。质能等价原理在核反应、粒子物理学和宇宙学中具有重要应用。

$E = m c^{2}$

因为相对论下的时空观与牛顿建立的时空观完全不同了，因此在相对论下的力学定律、电磁学定律、动量定律等都需要在相对论时空下重新推导，这里就不一一列举了。

其推导过程涉及洛伦兹变换即同一公式在不同坐标系下的表示形式，绝对的三维时空坐标系变换到相对的思维时空坐标系