IMU 误差模型及校准

分类于 Technology Blog ， Image ， Stabilization 阅读次数： Waline：本文字数： 4.7k 阅读时长 ≈ 17 分钟

传感器误差模型

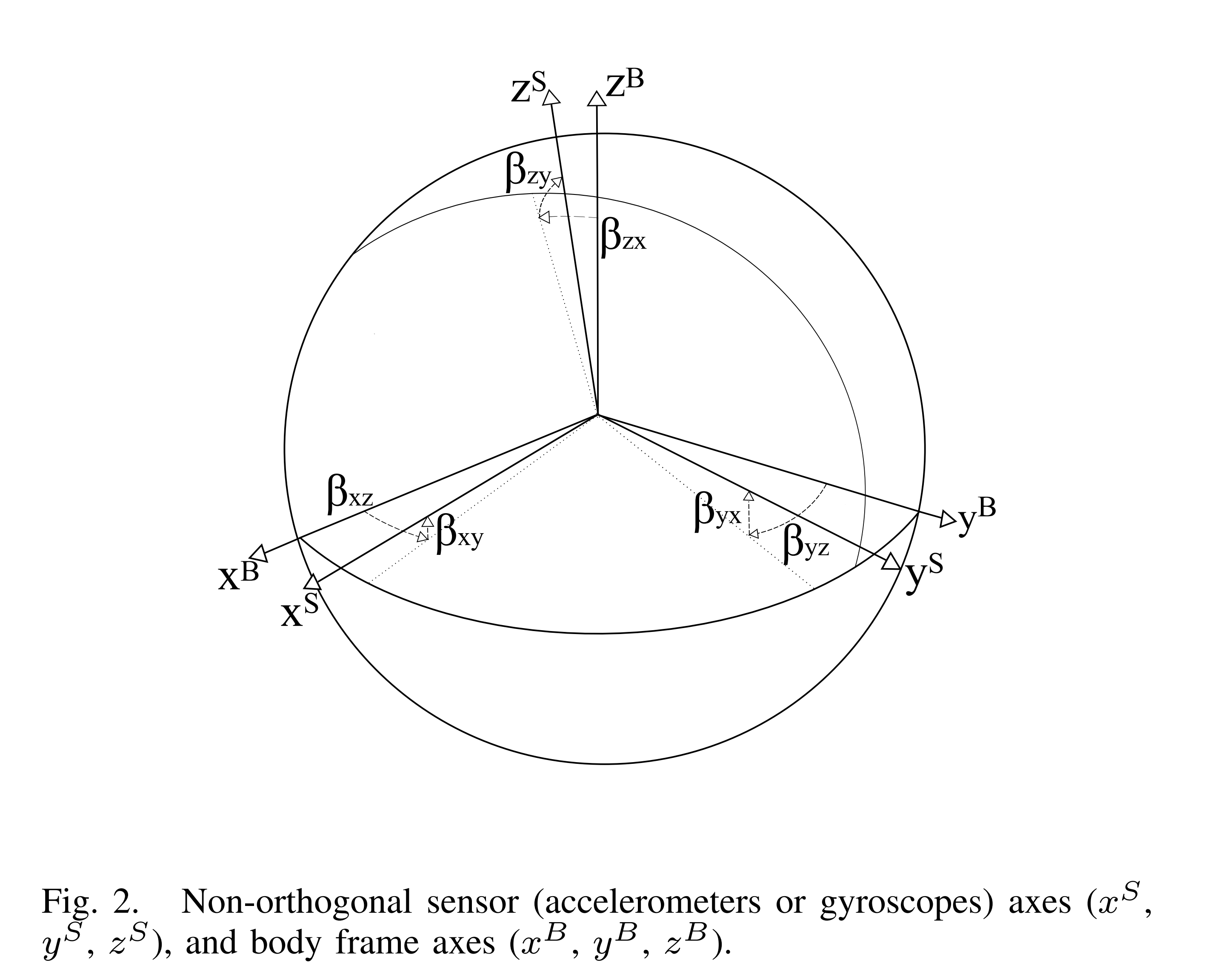
对于理想的 IMU 三轴加速度计两两正交，构成一个正交的三轴直角坐标系，加速度计每一轴单独测量该轴的加速度，而陀螺仪则测量该轴的角速度。在实际的真实 IMU 中由于制造工艺的误差，三个坐标轴不可能完全两两正交，加速度计与陀螺仪的坐标系也不会完全重合，并且单个传感器也不是完全精确的。在实际器件中将数字输出量转化为实际物理量的 scale 参数在不同轴上是不同的，但是设备生产商都会提供一个默认的 scale 参数用于转换所有轴的数据，而且数字量的输出还会受到零偏（传感器在静止情况下也会有微小量的输出）的影响，这些就是造成 IMU 传感器的系统误差。

我们取实际器件的加速度计坐标系为 AF, 陀螺仪坐标系为 GF，根据 AF 和 GF 分别建立对应的正交坐标系 AOF 和 GOF，其建立约束为

AOF 的 x 轴与 AF 的 x 轴重合。
AOF 的 y 轴位于 AF 的 x 与 y 轴的平面中。

对于 GOF 的建立约束与 AOF 的约束类比建立。最后再建立一个正交机体坐标系 BF，BF 通常与 AF 和 GF 之间有一个小角度的偏差。在非正交坐标系（AF 或 GF）中测量得到的物理量$s^S$可以转换到机体坐标系 BF 中得到$s^B$于是得到下式：

\[ s^B = Ts^S, T = \begin{bmatrix} 1 & -\beta_{yz} & \beta_{zy} \\ \beta_{xz} & 1 & -\beta_{zx} \\ -\beta_{xy} & \beta_{yx} & 1 \end{bmatrix} \tag{1} \]

$s^B 和 s^S$ 表示加速度或角速度在机体坐标系 BF 和加速度坐标系 AF 或陀螺仪坐标系 GF 下测量表示量，$\beta_{ij}$ 表示加速度或陀螺仪的 i 轴绕机体坐标系 BF 的 j 轴的旋转角度。如图二所示：

另外 BF 与 AOF 以及 BF 与 GOF 坐标系之间只有纯粹的旋转关系，我们假设 BF 的 x 轴恰巧与 AOF 的 x 轴重合在这种情况下$\beta_{xz},\beta_{xy},\beta_{yx}$变为 0 因此上一式可以写为如下：

\[ a^O = T^aa^S, T^a = \begin{bmatrix} 1 & -\alpha_{yz} & \alpha_{zy} \\ 0 & 1 & -\alpha_{zx} \\ 0 & 0 & 1 \end{bmatrix} \tag{2} \]

这里$a^O$和$a^S$表示加速度在 AOF 和 AF 坐标系下的表示。这里已经改变了$\beta$的含义，用$\alpha$来表示在 AF 与 AOF 的 x 轴重合的情况下 AF 与 AOF 各轴之间的旋转情况而不再是与机体坐标系 BF 之间的旋转关系了。如前所述，陀螺仪可以按照同样的方式进行定义，

\[ w^O = T^gw^S, T^g = \begin{bmatrix} 1 & -\gamma_{yz} & \gamma_{zy} \\ \gamma_{xz} & 1 & -\gamma_{zx} \\ -\gamma_{xy} & \gamma_{yx} & 1 \end{bmatrix} \tag{3} \]

注意到目前为止要重点区分 5 个坐标系，首先是加速度计坐标系 AF 和陀螺仪坐标系 GF 由于制造工艺的原因这两个坐标系都不是正交的，且这两个坐标系也不重合，然后根据 AF 和 GF 分创建了两个正交坐标系 AOF 和 GOF，建立的约束就是上文中提到的，最后又建立了一个机体坐标系。后面我们假设机体坐标系的 x 轴与加速度正交坐标系 AOF 的 x 轴重合于是建立了加速计方程（1）和（2）最后 BF 与 GOF 的 x 轴不重合因此只有第一步公式（3）没有后续的推导。

综上加速度计和陀螺仪的误差都是包含两部分比例误差 scale 和 0 偏误差 bias，比例偏差 scale 用如下表示：

\[ K^a = \begin{bmatrix} s_{a}^{x} & 0 & 0 \\ 0 & s_{a}^{y} & 0 \\ 0 & 0 & s_{a}^{z} \end{bmatrix}, K^g = \begin{bmatrix} s_{g}^{x} & 0 & 0 \\ 0 & s_{g}^{y} & 0 \\ 0 & 0 & s_{g}^{z} \end{bmatrix} \tag{4} \]

两个 bias 向量用如下表示：

\[ b^a = \begin{bmatrix} b_{a}^{x}\\ b_{a}^{y}\\ b_{a}^{z} \end{bmatrix}, b^g = \begin{bmatrix} b_{g}^{x}\\ b_{g}^{y}\\ b_{g}^{z} \end{bmatrix} \tag{5} \]

完整的加速度误差模型如下：

\[ a^O = T^aK^a(a^S + b^a + v^a) \tag{6} \]

完整的角速度误差模型如下：

\[ w^O = T^gK^g(w^S + b^g + v^g) \tag{7} \]

其中$v^a$和$v^g$不是系统误差是测量噪声。到此 IMU 的误差模型就讲清楚了，后面会基于这个误差模型进行建模校准传感器。

校准框架

为了校准加速度计我们需要估计如下未知参数：

\[ \theta^{acc} = [\alpha_{yz},\alpha_{zy},\alpha_{zx},s_{a}^{x},s_{a}^{y},s_{a}^{z},b_{a}^{x},b_{a}^{y}b_{a}^{z}] \tag{8} \]

我们定义如下函数：

\[ a^O = h(a^S,\theta_{acc}) = T^aK^a(a^S + b^a) \tag{9} \]

实际上是忽略了测量噪声。像传统的多位置方案中，我们移动 IMU 到 M 个不同的临时稳定状态，可以提取加速度向量$a_{k}^S$（在非正交坐标系 AF 中）计算加速度计在每个静止状态下的平均值，使用如下代价方程来估计加速度计的参数：

\[ L(\theta_{acc}) = \sum_{k=1}^{M}(||g||^2 - ||h(a_k^S,\theta_{acc})||^2)^2 \tag{10} \]

$||g||$是真实的当地重力加速度计，可以根据当地的经纬度非常容易的获取到，我们采用 Levenberg-Marquardt 方法来求取当代价函数的最小值时的参数。

为了校准陀螺仪我们可以在 IMU 初始的静止阶段读取陀螺仪数据并取均值，作为陀螺仪 bias。我们定义$\Psi$操作，用读取的陀螺仪数据$w_i^S$和重力向量$u_{a,k-1}$作为输入队列（重力向量是经过上面步骤校准过的）该操作返回最终的重力向量$u_{g,k}$。该操作可以是任意一个通过上一时刻加速度计与角速度计融合后得到当前重力向量的算法。

\[ u_{g,k} = \Psi(w_i^S,u_{a,k-1}) \tag{11} \]

我们需要估计的未知陀螺仪参数如下：

\[ \theta^{gyro} = [\gamma_{yz},\gamma_{zy},\gamma_{xz},\gamma_{zx},\gamma_{xy},\gamma_{yx},s_x^g,s_y^g,s_z^g] \tag{12} \]

在这种情况下我们定义代价函数：

\[ L(\theta_{gyro}) = \sum_{k=2}^M||u_{a,k} - u_{g,k}||^2 \tag{13} \]

M 是静态状态读取数据的数量$u_{a,k}$是加速度计计算得到的重力向量，$u_{g,k}$是通过（13）式计算得到的，我们要获得$\theta_{gyro}$的最小值同样采用上面提到的 Levenberg-Marquardt 方法来求取。

校准过程

静态检测

如前面校准框架所述，校准 IMU 需要收集加速度计和陀螺仪的原始数据，采集的数据应该包含 IMU 在各个稳定状态及其间隔状态下的数据。为了减小 bias 噪声对上面两个代价函数的影响需要先对 0 偏进行校准，初始阶段需要一段时间的静止用于校准陀螺仪的 bias 以及用于静态检测参考。

校准精度取决于对静止状态判断的准确性，校准加速度计需要在几个静态状态下进行运算，校准陀螺仪需要静态以及各个不同状态的静态之间的运动数据。根据经验对实际的数据集采用基于滤波的算子效果会较差，例如准静态检测器，检测静止状态通常会包含一些小的运动。而且基于滤波器的算法通常依赖滤波参数，需要对滤波参数进行调整。我们建议采用基于方差的静态检测器运算，他利用上面的静态检测间隔。我们的检测器基于$t_{wait}$时间间隔进行采集加速度信号并计算方差大小：

\[ \zeta(t) = \sqrt{[var_{t_w}(a_x^t)]^2 + [var_{t_w}(a_y^t)]^2 + [var_{t_w}(a_z^t)]^2} \tag{14} \]

其中$var_{t_w}(a^t)$是以时间 t 为中心每隔时间间隔$t_w$加速度信号的方差值，我们要对该状态进行分类为静止还是运动只需要对$\zeta(t)$跟一个阈值进行比较就可以了。这个阈值我们可以选取 IMU 在初始静止状态下的值$\zeta(init)$，从而不依赖任何外部参数的调整。

龙格库塔法积分

在上面的 11 式中，通过 k-1 时刻的加速度计得到的重力向量与 k-1 到 k 时刻的加速度进行运算得到 k 时刻的重力向量，这里 k-1 和 k 是两个稳定状态，因此 k-1 和 k 之间有一段时间的运动，需要对陀螺仪数据进行积分到加速度计的重力向量中去，在我们的实验中采用 4 阶龙格库塔积分法（RK4n）比标准线性积分精度要高，下式 15 用微分方程来描述四元数运动方程：

\[ f(q,t) = \dot{q} = \frac{1}{2}\Omega(w(t))q \tag{15} \]

这里 q 是 t-1 时刻的重力向量的四元数表示，而$\Omega(w)$是将角速度转化为斜对称旋转矩阵的操作，形式如下：

\[ \Omega(w) = \begin{bmatrix} 0 & -w_x & -w_y & -w_z \\ w_x & 0 & w_z & -w_y \\ w_y & -w_z & 0 & w_x \\ w_z & w_y & -w_x & 0 \end{bmatrix} \tag{16} \]

RK4n 算法如下：

\[ q_{k+1} = q_k + \Delta t \frac{1}{6} (k_1 + 2k_2 + 2k_3 + k_4) \tag{17} \]

\[ k_i = f(q^{(i)},t_k + c_i\Delta t) \tag{18} \]

\[ q^{(i)} = q_k, for i = 1 \tag{19} \]

\[ q^{(i)} = q_k + \Delta t \sum_{j=1}^{i-1}a_{ij}k_j, for i>1 \tag{20} \]

所有需要的系数$c_i$和$a_{ij}$为：

\[ c_1 = 0, c_2 = \frac{1}{2}, c_3 = \frac{1}{2},c_4 = 1, \\ a_{21} = \frac{1}{2}, a_{31} = 0, a_{41} = 0, \\ a_{32} = \frac{1}{2}, a_{42} = 0, a_{43} = 1. \]

最后对于每一步我们需要归一化四元数 q：

\[ q_{k+1} \rightarrow \frac{q_{k+1}}{||q_{k+1}||} \tag{21} \]

阿伦方差

我们使用艾伦方差来表示陀螺仪的随机漂移误差，这里用$\delta_a^2$来衡量连续间隔陀螺仪数据平均值之间的方差：

\[ \delta_a^2 = <(x(\tilde{t},k) - x(\tilde{t},k-1))^2> \\ =\frac{1}{2K}\sum_{k=1}^K(x(\tilde{t},k) - x(\tilde{t},k-1))^2 \tag{22} \]

其中$x(t,k)$是第 k 个$\tilde{t}$时间间隔陀螺仪数据的均值，K 是所有时间的$\tilde{t}$个数，我们对每一个轴计算阿伦方差，当阿伦方差收敛到很小的一个值时就表示校准 ok 了，在初始阶段我们将对陀螺仪数据进行求阿伦方差进行校准。

完成校准

为了得到较好的校准结果至少需要 9 种不同姿态的数据，实验表明姿态数越多校准结果越好。

附录

Levenberg-Marquardt 算法

牛顿法

牛顿法（英语：Newton's method）又称为牛顿-拉弗森方法（英语：Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数$f(x)$的泰勒级数的前面几项来寻找方程$f(x)=0$的根。算法过程：首先选择一个接近函数$f(x)$零点的$x_0$, 计算相应的$f(x_0)$和切线斜率${f}'(x_0)$，然后计算穿过点$(x_0,f(x_0))$并且斜率为${f}'(x_0)$的直线和$x$轴的交点的$x$坐标，也就是求如下方程的解：

\[ 0 = (x - x_0)\cdot f'(x_0) + f(x_0) \]

我们求解 x，过程如下：

\[ 0 = (x - x_0) + \frac{f(x_0)}{f'(x_0)} x - x_0 = - \frac{f(x_0)}{f'(x_0)} x = x_0 - \frac{f(x_0)}{f'(x_0)} \]

我们将新求得的点$x$坐标命名为$x_1$，通常$x_1$会比$x_0$更接近方程$f(x) = 0$的解，因此我们可以利用$x_1$开始下一轮的迭代，迭代公式如下：

\[ x_{n+1} = x_n - \frac {f(x_n)}{f'(x_n)} \]

对于多维的情况，对$f(x)$在$x_0$处进行二阶泰勒展开：

\[ f(x) = f(x_0) + \bigtriangledown f(x_0)^T(x - x_0) + \frac{1}{2}(x - x_0)^TH(x_0)(x - x_0) \]

这里$\bigtriangledown f(x_0)$是$f(x)$的梯度向量在点$x_0$处的值；$H(x_0)$是$f(x)$的海塞矩阵在点$x_0$处的值，函数$f(x)$有极值的必要条件是在极值点处一阶导数为 0. 利用极小点的必要条件$\bigtriangledown f(x_k) = 0$每次迭代从$x_k$开始求目标函数的极小点，作为第$k+1$次迭代值$x_{k+1}$ 假如$x_{k+1}$满足$\bigtriangledown f(x_{k+1}) = 0$对$\bigtriangledown f(x)$进行泰勒展开：

\[ \bigtriangledown f(x) = \bigtriangledown f(x_k) + H(x_k)(x - x_k) \\ \bigtriangledown f(x_k) + H(x_k)(x_{k+1} - x_k) = 0 x_{k+1} = x_k - H(x_k)^{-1} \bigtriangledown f(x_k) \]

可以写为如下：

\[ x_{k+1} = x_k - H_k^{-1}g_k \]

这就是牛顿法的多维公式，其中$g_k = \bigtriangledown f(x_k)$

高斯-牛顿法

给定 m 个方程$\textbf{r} = (r_1,r_2,...r_m)$（通常叫做残差方程）和 n 个变量$\beta = (\beta_1,\beta_2,...\beta_n)$, 其中$m \geqslant n$, 高斯-牛顿算法迭代找出下式取最小值时的最优值。

\[ s(\beta) = \sum_{i=1}^{m}r_i(\beta)^2 \]

从给定初始值$\beta_0$开始，通过下式进行迭代寻找$s(\beta)$的最小值：

\[ \beta_{s+1} = \beta_{s} - (J_rJ_r)^{-1} J_r^T r \beta_s \]

这里$r$和$\beta$都是列向量，$J_r$Jacobian matrix 为：

\[ (J_r)_{ij} = \tfrac{\partial r_i \beta_s}{\partial \beta_j} \]

其中符号$^T$是 matrix transpose. 如果 m=n 则可以简化为如下：

\[ \beta_{s+1} = \beta_{s} - (J_r)^{-1} r \beta_s \]

这就是一维牛顿法的直接推广。在数据拟合中，目标是找到最佳参数$\beta$使得$\beta$满足给定模型$y = f(x,\beta)$可以最好的符合数据点$(x,y)$, 方程$r$是残差方程，如下：

\[ r_i(\beta) = y_i - f(x_i, \beta) \]

高斯-牛顿法可以用函数$f$的雅克比$J_f$表示：

\[ \beta_{s+1} = \beta_{s} - (J_fJ_f)^{-1} J_f^T r \beta_s \]

这里$(J_fJ_f)^{-1} J_f^T$是$J_f$的伪逆（摩尔-彭罗斯逆）。

高斯-牛顿算法将通过近似从牛顿方法优化函数中推导而来。牛顿方法最小化参数函数$s$的递归关系$\beta$为：

\[ \beta_{s+1} = \beta_s - H^{-1}g \] 其中$g$表示$S$梯度向量，$H$表示$S$的海塞矩阵 ( Hessian matrix). 由于$S =\sum_{i=1}^{m}r_i \frac{\partial r_i}{\partial \beta_j}$其梯度通过下式给出：

\[ g_{j}=2\sum _{i=1}^{m}r_{i}{\frac {\partial r_{i}}{\partial \beta _{j}}} \]

海塞矩阵$H$的元素通过梯度$g_j$的不同元素$\beta_k$计算得到：

\[ H_{jk}=2\sum _{i=1}^{m}\left({\frac {\partial r_{i}}{\partial \beta _{j}}}{\frac {\partial r_{i}}{\partial \beta _{k}}}+r_{i}{\frac {\partial ^{2}r_{i}}{\partial \beta _{j}\partial \beta _{k}}}\right) \]

高斯-牛顿法忽略二阶小项，海塞矩阵$H$可以近似写为：

\[ H_{jk}\approx 2\sum _{i=1}^{m}J_{ij}J_{ik} \]

这里$J_{ij}={\frac {\partial r_{i}}{\partial \beta _{j}}}$是雅克比矩阵$J_r$的一项，梯度和海塞矩阵可以通过如下符号来表示：

\[ \mathbf {g} =2{\mathbf {J} _{\mathbf {r} }}^{\mathsf {T}}\mathbf {r} ,\quad \mathbf {H} \approx 2{\mathbf {J} _{\mathbf {r} }}^{\mathsf {T}}\mathbf {J_{r}} \]

将这些表达式代入上述递归关系中以获得运算方程式就得到：

\[ {\boldsymbol {\beta }}_{(s+1)}={\boldsymbol {\beta }}_{(s)}-\left(\mathbf {J_{r}} ^{\mathsf {T}}\mathbf {J_{r}} \right)^{-1}\mathbf {J_{r}} ^{\mathsf {T}}\mathbf {r} \left({\boldsymbol {\beta }}_{(s)}\right) \]

注意并非在所有情况下都保证高斯-牛顿法的收敛性，下式要能够得到保证才可以：

\[ \left|r_{i}{\frac {\partial ^{2}r_{i}}{\partial \beta _{j}\partial \beta _{k}}}\right|\ll \left|{\frac {\partial r_{i}}{\partial \beta _{j}}}{\frac {\partial r_{i}}{\partial \beta _{k}}}\right| \]

二阶导数足够小可以被忽略，在如下两种情况下都会收敛：

1.$r_i$在选取值附近要足够小，至少在最小值附近要足够小。 2. 函数只有轻度的非线性，因此$ $在选取值附近才会足够小。

Levenberg-Marquardt 算法

莱文贝格－马夸特方法（Levenberg–Marquardt algorithm）能提供数非线性最小化（局部最小）的数值解。、和其他最小化算法一样，LM 算法也是采用迭代过程，首先也是要提供一个参数$\beta$的猜测值，在只有一个最小值的情况下初始猜测参数为${\boldsymbol {\beta }}^{\text{T}}={\begin{pmatrix}1,\ 1,\ \dots ,\ 1\end{pmatrix}}$也可以很好的工作，在有多个极小值的情况下仅当猜测值以及接近最终解时，算法才会收敛到全局最小值。在每一步迭代中参数向量$\beta$用新的评估值$\beta + \delta$替代之前的值，为了确定$\delta$函数${\displaystyle f\left(x_{i},{\boldsymbol {\beta }}+{\boldsymbol {\delta }}\right)}$需要近似线性化。

\[ f\left(x_{i},{\boldsymbol {\beta }}+{\boldsymbol {\delta }}\right)\approx f\left(x_{i},{\boldsymbol {\beta }}\right)+\mathbf {J} _{i}{\boldsymbol {\delta }} \]

其中：

\[ \mathbf {J} _{i}={\frac {\partial f\left(x_{i},{\boldsymbol {\beta }}\right)}{\partial {\boldsymbol {\beta }}}} \]

是函数$f$对参数$\beta$的梯度。 $s(\beta)$ 平方偏差之和在 $f$对$\beta$ 的梯度为 0 时取最小值，上面是 $f\left(x_{i},{\boldsymbol {\beta }}+{\boldsymbol {\delta }}\right)$ 的一阶近似，则：

\[ S\left({\boldsymbol {\beta }}+{\boldsymbol {\delta }}\right)\approx \sum _{i=1}^{m}\left[y_{i}-f\left(x_{i},{\boldsymbol {\beta }}\right)-\mathbf {J} _{i}{\boldsymbol {\delta }}\right]^{2} \]

或者用向量符号表示：

\[ {\begin{aligned}S\left({\boldsymbol {\beta }}+{\boldsymbol {\delta }}\right)&\approx \left\|\mathbf {y} -\mathbf {f} \left({\boldsymbol {\beta }}\right)-\mathbf {J} {\boldsymbol {\delta }}\right\|^{2}\\&=\left[\mathbf {y} -\mathbf {f} \left({\boldsymbol {\beta }}\right)-\mathbf {J} {\boldsymbol {\delta }}\right]^{\mathrm {T} }\left[\mathbf {y} -\mathbf {f} \left({\boldsymbol {\beta }}\right)-\mathbf {J} {\boldsymbol {\delta }}\right]\\&=\left[\mathbf {y} -\mathbf {f} \left({\boldsymbol {\beta }}\right)\right]^{\mathrm {T} }\left[\mathbf {y} -\mathbf {f} \left({\boldsymbol {\beta }}\right)\right]-\left[\mathbf {y} -\mathbf {f} \left({\boldsymbol {\beta }}\right)\right]^{\mathrm {T} }\mathbf {J} {\boldsymbol {\delta }}-\left(\mathbf {J} {\boldsymbol {\delta }}\right)^{\mathrm {T} }\left[\mathbf {y} -\mathbf {f} \left({\boldsymbol {\beta }}\right)\right]+{\boldsymbol {\delta }}^{\mathrm {T} }\mathbf {J} ^{\mathrm {T} }\mathbf {J} {\boldsymbol {\delta }}\\&=\left[\mathbf {y} -\mathbf {f} \left({\boldsymbol {\beta }}\right)\right]^{\mathrm {T} }\left[\mathbf {y} -\mathbf {f} \left({\boldsymbol {\beta }}\right)\right]-2\left[\mathbf {y} -\mathbf {f} \left({\boldsymbol {\beta }}\right)\right]^{\mathrm {T} }\mathbf {J} {\boldsymbol {\delta }}+{\boldsymbol {\delta }}^{\mathrm {T} }\mathbf {J} ^{\mathrm {T} }\mathbf {J} {\boldsymbol {\delta }}.\end{aligned}} \]

这里暂时先不做理论推导了，目前没找到好的推导方法，直接上结论吧，

\[ (\mu \mathbf {I}+(\mathbf {J}^{T}\mathbf {J})) \delta _{p}=\mathbf {J}^{T}\epsilon_k \]

就是莱文贝格－马夸特方法。如此一来 $\mu$ 大的时候这种算法会接近最速下降法，小的时候会接近高斯-牛顿方法。为了确保每次 $\mathbf {\epsilon }$ 长度的减少，我们这么作：先采用一个小的 $\mu$ ，如果 $\mathbf {\epsilon }$ 长度变大就增加 $\mu$ 。这个算法当以下某些条件达到时结束迭代：

如果发现 ${\mathbf {\epsilon }}$ 长度变化小于特定的给定值就结束。
发现 ${\mathbf {\delta _{p}}}$ 变化小于特定的给定值就结束。
到达了迭代的上限设定就结束。

参考文献

《A Robust and Easy to Implement Method for IMU Calibration without External Equipments》