使用陀螺仪的数字视频稳定和卷帘快门校正

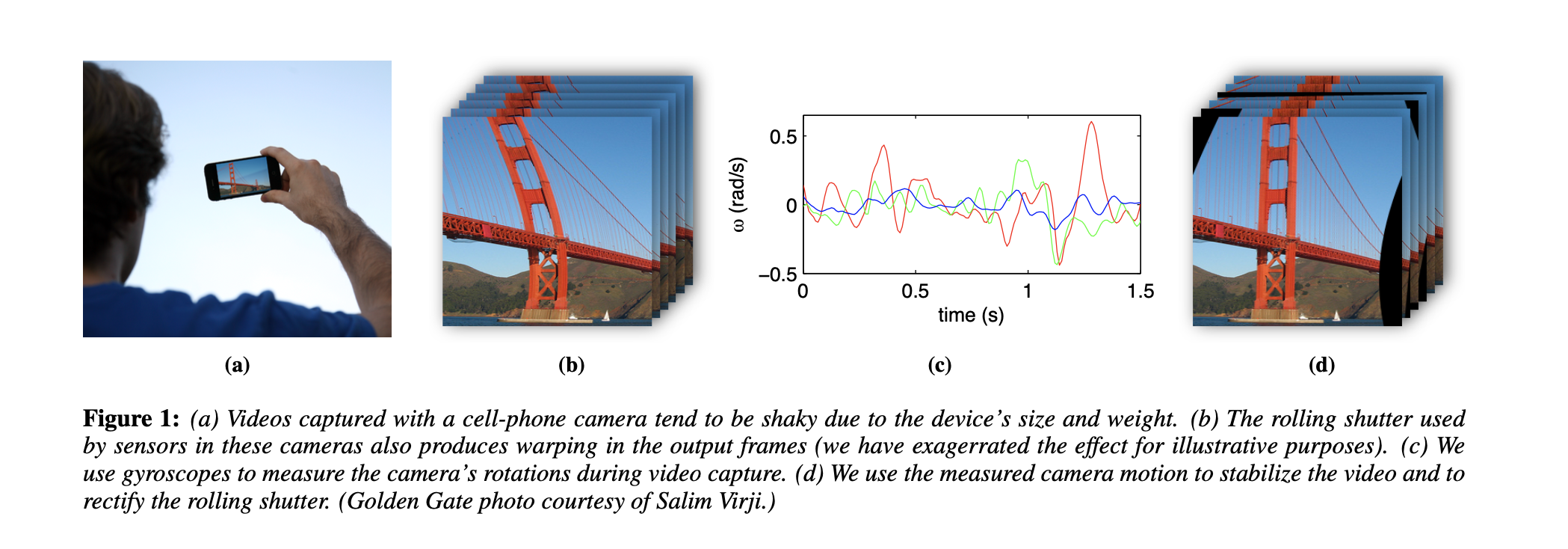
Abstract

在本文中，我们提出了一种基于商用陀螺仪的强大实时视频稳定和滚动快门校正技术。首先来对相机运动和卷帘快门扭曲进行建模，然后从单个视频捕获自动校准陀螺仪和相机输出。 这种校准使我们能够仅使用陀螺仪数据来有效校正卷帘快门扭曲并稳定视频。

Video Stabilization and Rolling Shutter Correction

我们系统中的相机运动仅根据旋转进行建模。 我们忽略平移运动，加速度计数据必须被积分两次才能获得位移，因此它们很难使用 IMU 准确测量。即使我们可以准确地测量平移，这也是不够的，因为在相机相同平移量的情况下不同深度的物体移动的量不同，我们将不得不依赖立体或基于特征的运动结构（SfM）算法来获取深度信息。这些方法并不健壮，而且目前在移动平台上实时运行计算成本太高。

Forsse ́n 和 Ringaby[2010] 试图在他们的系统中模拟相机位移，但发现结果比只考虑旋转的模型表现更差。 他们假设优化器在尝试从特征跟踪器重建位移时陷入局部最小值。他们的算法还假设相机正在对纯平面场景（即恒定深度）进行成像。 因此，由于视频中的未建模视差，平移重建有时会失败。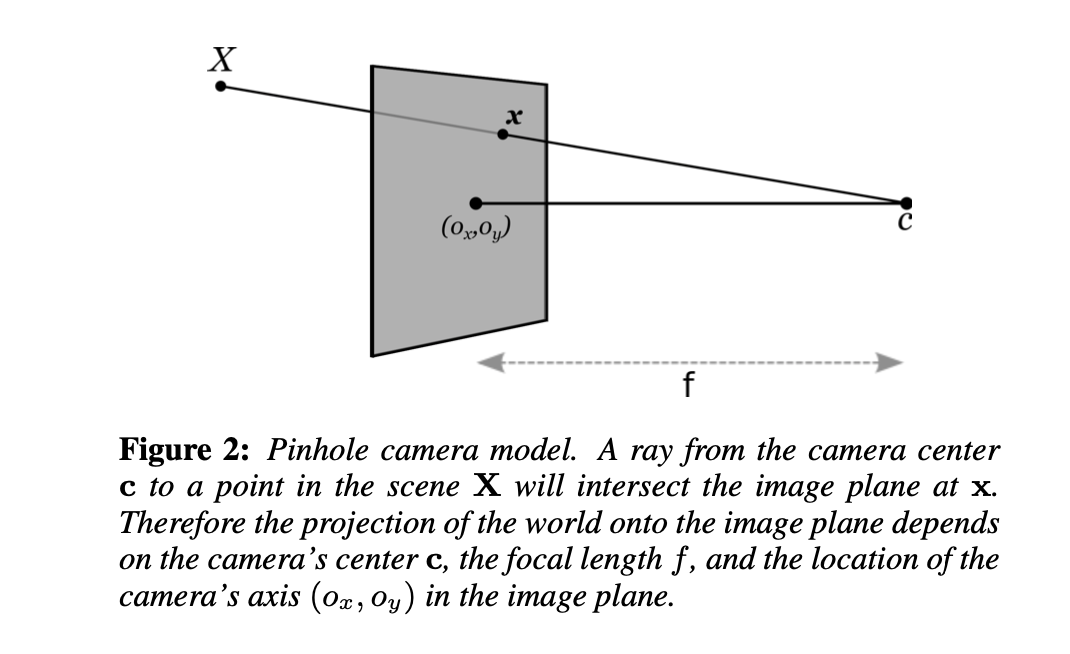

为了避免这些问题，我们没有将平移合并到我们的模型中。 幸运的是，相机抖动和卷帘快门扭曲主要来自旋转。之所以如此，是因为平移随着深度的增加而迅速衰减，并且物体通常离镜头足够远，平移相机抖动不会在图像中产生明显的运动。 这一结论得到了我们的稳定结果的支持。

Camera Model

我们的旋转卷帘快门相机模型基于针孔相机模型。在针孔相机中，图像之间的关系在齐次坐标中的点 x 和对应点在 3D 世界坐标系中的 X（图 2）可以通过以下方式表示：

\[ x=KX, X=\lambda K^{-1}x \tag1 \]

其中\(\lambda\)是未知比例因子，\(K\)是相机内参矩阵，我们假定内参矩阵的逆如下：

\[ K^{-1} = \begin{bmatrix} 1 & 0 & -o_x\\ 0 & 1 & -o_y\\ 0 & 0 & f \end{bmatrix} \tag2 \]

其中，\((o_x, o_y)\) 是图像平面中相机轴的原点坐标，f 是焦距。

Camera Motion

我们将世界原点设置在相机原点。然后可以用 R(t) 来描述相机在时间 t 时刻的运动。因此，对于任何世界坐标点点 X，对应的图像点 x 在时间 t 由下式给出：

\[ x = KR(t)X \tag3 \]

旋转矩阵\(R(t) \in SO(3)\)是通过相机旋转角度\(\Delta \theta (t)\)计算得到的。然后对其使用 SLERP（球形四元数线性插值）来平滑的得到足够多的旋转矩阵。\(\Delta \theta (t)\)可以通过陀螺仪的角速度获得：

\[ \Delta \theta (t) = (w(t + t_d) + w_d) * dt \tag4 \]

这里\(w_d\)是陀螺仪漂移，\(t_d\)是陀螺仪和相机时间戳的差，这些参数都是未知的需要进行校准获得。

Rolling Shutter Compensation

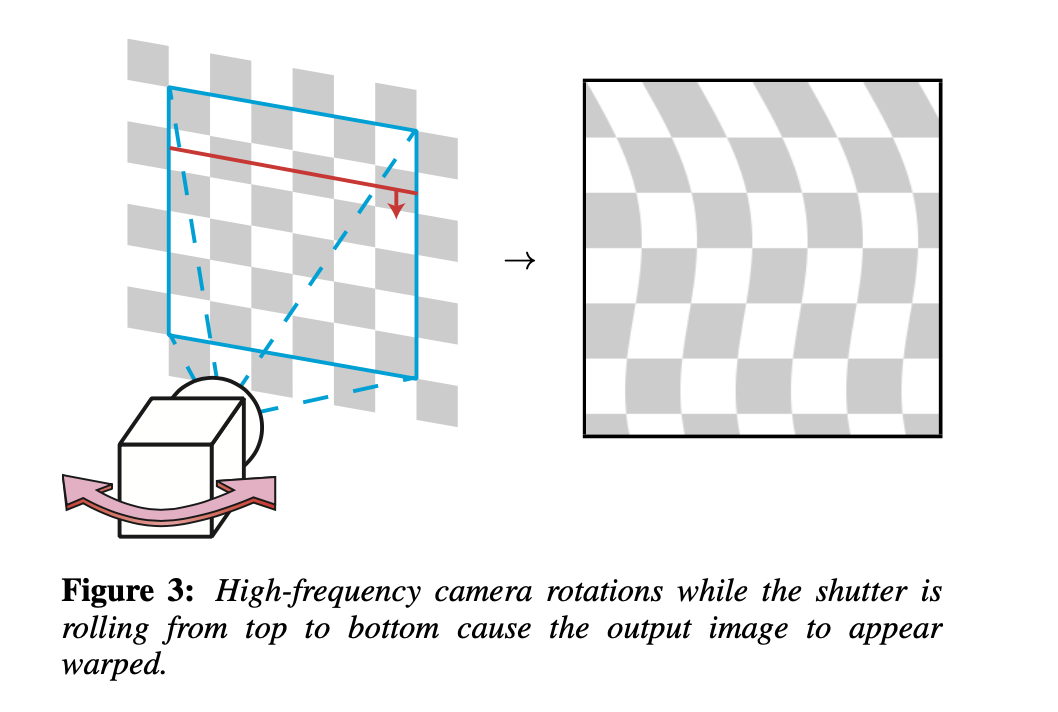
我们现在将卷帘快门的概念引入我们的相机模型中。在 RS 相机中，每个图像行的曝光时间略有不同，因此曝光期间相机的旋转将导致图像的扭曲。例如，如果相机在快门滚动时左右摇摆，则输出图像将扭曲，如图 2 所示。更正式地说，我们可以说 x 在时间 t(i, y) 期间成像：

\[ t(i,y) = t_i + t_s * y / h; where x = (x,y,1)^T \tag5 \]

其中 y 是点 x 对应的图像行，h 是帧中的总行数，\(t_i\)是第 i 帧的时间戳。 \(t_s\)是一帧曝光所需时间，也就是从上到下逐行读出完整帧所需的时间。

Image Warping

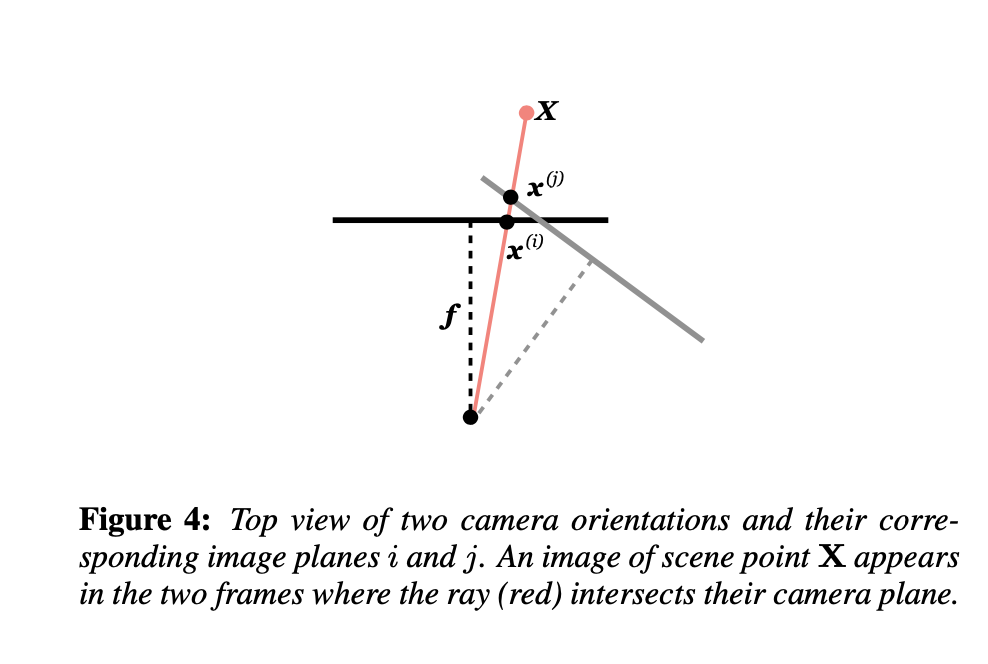
现在我们推导出一帧图像两个坐标点之间的旋转关系。对于场景点 X，在 i 帧和 j 帧的图像平面中的投影点\(x_i\)和\(x_j\)由下式给出：

\[ x_i = KR(t(i,y_i))X, and x_j = KR(t(j,y_j))X \tag6 \]

联立两式整理得到：

\[ x_j = KR(t(j,y_j))R^{T}(t(i,y_i))K^{-1}x_i \tag7 \]

想在我们已经考虑了同一个视频中的两帧之间的关系，我们加入限制条件两帧图像的原点相同，将\(R(t)\)映射到\(R'(t)\), 现在重新定义扭曲矩阵将一个点映射到另一个相机坐标系下：

\[ W(t1,t2) = KR'(t1)R^T(t2)K^{-1} \tag8 \]

我们可以得到如下：

\[ x_j = W(t(j,y_j),t(i,y_i))x_i, R' = R \tag9 \]

还要注意，W 分别取决于图像点\(x_i\)和\(x_j\)的图像行\(y_i\)和\(y_j\)。该变换矩阵可用于将帧 i 中的点与帧 j 中的对应点进行匹配，同时在两帧中都考虑卷帘快门的影响。给定这种变形矩阵的公式，滚动快门校正和视频稳定的算法就变得简单了。我们创建了一个具有平滑运动和全局快门的合成视频。该相机的运动是通过对输入相机的运动应用高斯低通滤波器来计算的，这会产生一组新的旋转矩阵 R0。我们将合成相机的滚动快门持续时间 ts 设置为 0（即全局快门），然后我们在当前帧 i 的每个图像行\(y_i\)处计算\(W(t_i; t(i; y_i))\)，并将扭曲应用于该行。 请注意 W 的第一项现在仅取决于帧时间\(t_i\)。此操作将所有输入帧映射到我们的合成视频上；因此可以同时消除滚动快门扭曲和视频抖动。

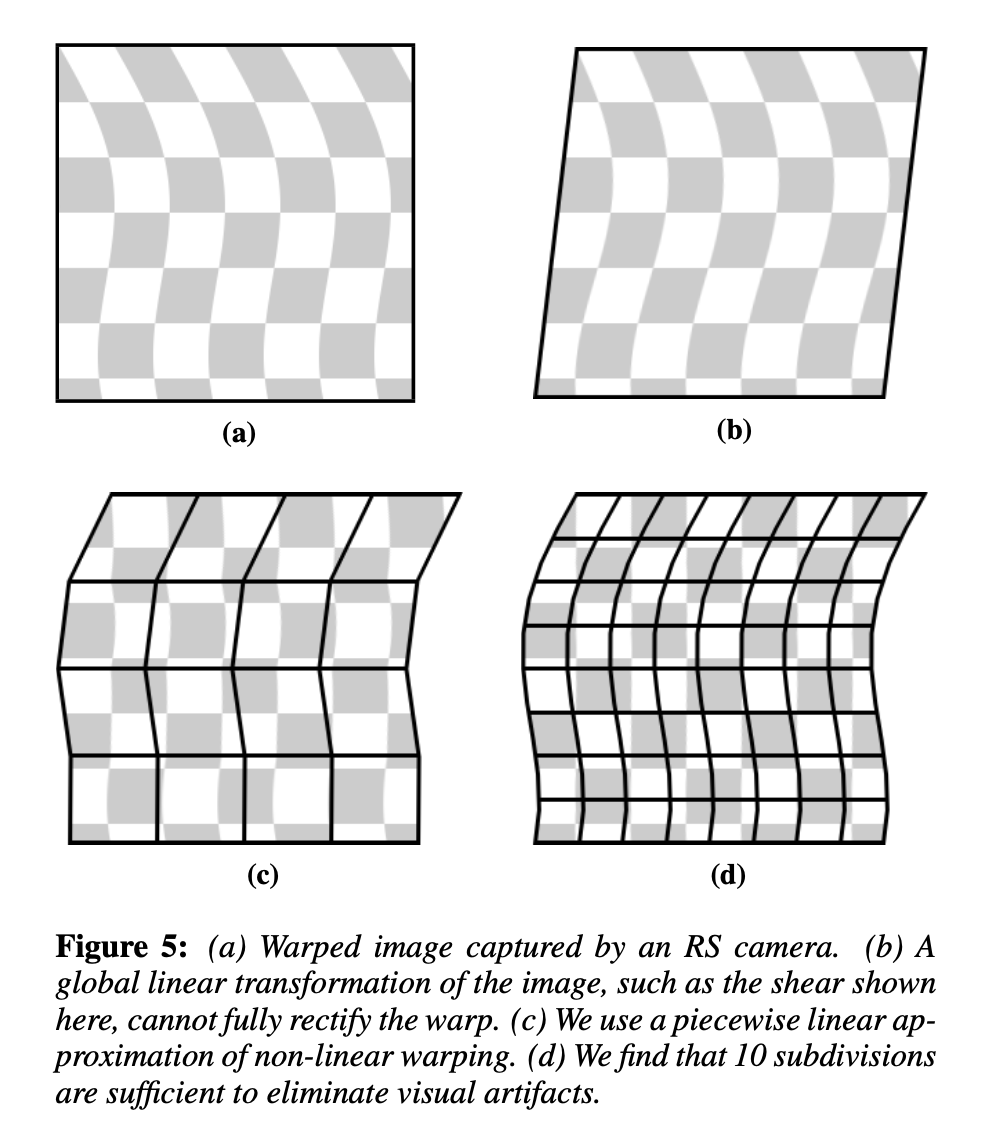
实际上，我们不会为每个图像行\(y_i\)计算\(W(t_i; t(i; y_i))\)。相反我们细分输入图像（图 5a）并计算每个垂直细分的扭曲（图 5c 和 5d）。本质上，我们从输入图像创建一个扭曲的网格，它是非线性扭曲的分段线性近似。我们发现十个细分通常足以去除任何可见的 RS 拖影。Forssen 和 Ringaby [2010] 将这种采样方法称为´逆插值。他们还提出了两种额外的插值技术，他们凭经验证明在合成视频数据集上表现更好。然而，我们使用逆插值是因为使用顶点着色器很容易在 GPU 上实现一个高效的版本。GPU 的片段着色器负责使用双线性插值对网格扭曲图像进行重新采样。我们发现，由于双线性逆插值实际视频中的 RS 扭曲通常不足以产生混叠拖影，因此逆插值在实践中效果也很好。

Camera and Gyroscope Calibration

我们现在展示用于找到未知的相机和陀螺仪参数。 这个校准步骤是必要的，它使我们能够直接从陀螺仪数据中计算 W。 我们模型中的未知参数是：相机的焦距 f、滚动快门的持续时间 \(t_s\)、陀螺仪和帧样本时间戳之间的延迟 \(t_d\) 以及陀螺仪漂移 \(w_d\)

请注意，制造商可能会给定其中一些参数，例如相机的焦距，也可以通过实验测量这些参数。 例如，Forssen 和 Ringaby [2010] 使用快速闪烁的显示器来测量滚动快门持续时间 \(t_s\)。 然而这些技术往往不精确且容易出错；而且它们也太繁琐，普通用户无法执行。滚动快门的持续时间通常在毫秒范围内。因此，\(t_d\) 或\(t_s\)中的小偏差将导致卷帘门整流失败。

我们的方法是从单个视频和陀螺仪捕获中估计这些参数。用户被要求记录视频和陀螺仪轨迹，在那里他们站着不动并在指向建筑物时晃动相机。持续时间约为 10 秒的短片通常以估计所有未知数。 请注意，这只需为每个摄像头和陀螺仪设置完成一次。

在我们的方法中，我们使用 SIFT [Lowe 2004] 在连续视频帧中找到匹配点，并且我们使用 RANSAC [Fischler and Bolles 1981] 来丢弃异常值。 结果是捕获视频中所有相邻帧的一组点对应关系 \(x_i\) 和 \(x_j\) （图 6）。鉴于这一基本事实，我们可以将校准表述为一个优化问题，我们希望最小化所有点对应的均方重投影误差：

\[ J = \sum_{i,j} \left \| x_j - W(t(j,yj); t(i, yi))x_i \right \|^2 \tag{10} \]

请注意，这是一个非线性优化问题。许多非线性优化器可用于最小化我们的目标函数。 然而，我们发现通过直接目标函数评估的坐标下降可以快速收敛。每次我们在目标函数 J 不减小的情况下迈出一步，我们就反转步长方向并减小相应参数的步长。一旦所有参数的步长降到所需阈值以下（即，当我们达到目标精度时），算法就会终止。对于时长约 10 秒的校准视频，我们的 Matlab/C++ 实现通常会在 2 秒内收敛。

我们通过将焦距设置为相机具有 45° 的视野来初始化优化算法，并将所有其他参数设置为 0。我们发现在这些初始条件下，优化器收敛到我们数据集的正确解。 更一般地，我们可以通过重新启动我们的坐标下降算法以获取一系列合理参数并选择最佳解决方案来避免陷入局部最小值（例如，当陀螺仪和帧时间戳之间的延迟很大时）。正确恢复参数的平均重新投影误差通常约为 1 个像素。

我们模型中的另一个未知数是陀螺仪与相机的相对方向。 例如，绕陀螺仪 y 轴的旋转可以对应于绕相机 x 轴的旋转。为了发现陀螺仪的方向，我们排列了它的 3 个旋转轴并为每个排列运行我们的优化器，最小化目标的排列最好对应于相机的轴顺序。我们发现不正确排列的重投影误差要大得多。 因此，这种方法在实践中效果很好。

在我们的讨论中，我们假设相机具有垂直滚动快门。RS 模型可以很容易地修改为适用于图像列而不是行。 找到两种情况下的最小重投影误差将告诉我们相机是否具有水平或垂直滚动快门。

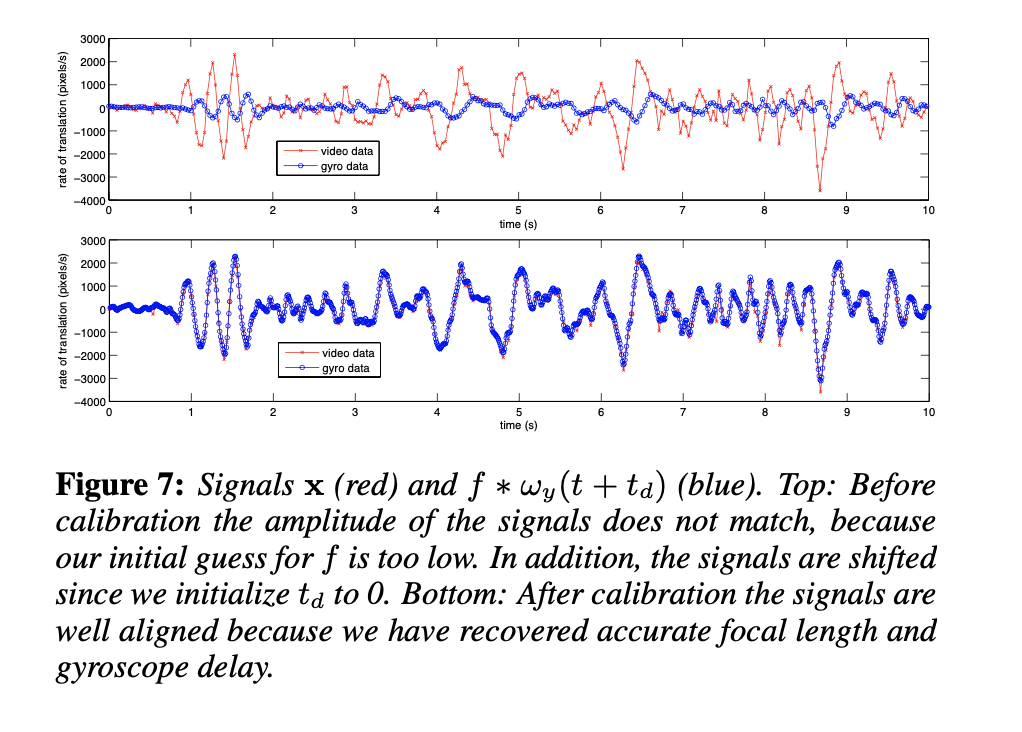
最后，为了更好地了解校准所获得的结果，我们展示了校准前后视频和陀螺仪信号的可视化效果。 如果我们假设连续帧之间的旋转很小，那么图像中的平移可以通过旋转近似计算如下：

\[ \dot{x} \approx f * \hat{\omega }(t+t_d), where \left\{\begin{matrix} \dot{x} = (\dot{x},\dot{y})^T\\ \dot{y} = (w_y,w_x)^T \end{matrix}\right. \tag{11} \]

在这里，我们还假设滚动快门没有影响（即 \(t_s\) = 0），并且我们忽略绕 z 轴的旋转（即 \(\omega_z\)）。 我们让 \(\dot{x}\) 是连续帧中所有点对应沿 x 和 y 的平均平移率。 如果我们的优化器收敛到正确的焦距 f 和陀螺延迟 \(t_d\)，那么两个信号应该对齐。 图 7 绘制了对齐前后信号 \(\dot{x}\) 和 \(f ∗ \hat{\omega }(t + t_d)\) 的第一维。 请注意陀螺仪数据与图像运动的匹配程度。 MEMS 陀螺仪的这种惊人的精度使我们的方法能够在视频稳定和滚动快门校正任务上表现良好。

参考文献

< Digital Video Stabilization and Rolling Shutter Correction using Gyroscopes >