基于陀螺仪的视频稳定非线性滤波器

Abstract

我们提出了一种对移动设备上捕获的视频进行视频稳定和滚动快门校正的方法。该方法使用来自机载陀螺仪的数据来跟踪相机的角速度，并且可以在相机捕获期间内实时运行。我们消除了由于手抖动引起的小抖动和滚动快门失真，营造出在三脚架上拍摄的视频的效果。

Introduction

大多数中高端移动设备包含一个多核 CPU 复合体、一个图形处理单元 (GPU) 和一个带有 3 轴陀螺仪的惯性测量单元 (IMU)。 在本文中，我们解决了在此类设备上执行视频稳定的挑战，使用陀螺仪进行运动跟踪。 与大多数稳定方法不同，它们作为捕获视频的后处理步骤运行，我们的方法可以作为相机捕获的一部分实时运行。

Background and Prior Work

视频稳定消除了视频中的抖动，它本质上是一个三阶段过程，包括运动估计阶段、平滑测量运动的滤波阶段和生成新视频序列的重新合成阶段。

当深度变化引起像素运动时，基于图像的跟踪方法会受到影响，视差，单应性不容易建模。此外，滚动快门成像传感器可以引入非刚性的帧到帧对应关系，不能简单地通过全局帧到帧运动模型进行建模。为了解决滚动快门问题，Baker 等人 [8] 使用低频光流的时间超分辨率估计和去除相机的高频抖动。Grundmann 等人 [3] 开发了一个基于混合单应性的模型，该模型跟踪帧内运动并生成具有校正滚动快门失真的稳定视频。 Liu 等人 [6] 采用基于网格的空间变化运动表示，结合自适应时空路径优化，可以处理视差并校正滚动快门效应。

Karpenko [1] 和 Hanning 等人 [11] 描述了使用内置陀螺仪跟踪相机方向的移动设备的视频稳定技术，将线性低通滤波器应用于陀螺仪输出。Karpenko 等人 [1] 使用高斯核，而 Hanning 等人 [11] 应用可变长度的 Hann 窗口来自适应地平滑相机路径。相比之下，我们引入了一种非线性滤波方法，该方法可以完全平坦化小运动，而不管频率如何，并在虚拟摄像机必须移动以将裁剪窗口保持在输入帧内时执行低通平滑。当相机几乎静止时，我们的虚拟相机被固定，消除所有抖动。移动时，我们的方法就像一个可变 IIR 滤波器，以平滑输出的方式将输入速度与虚拟相机速度混合，同时保证它跟踪输入，以便裁剪窗口永远不会离开输入帧。

Algorithm Description

从概念上讲，可以通过创建一个裁剪矩形来实现视频稳定，该矩形在相机四处晃动时随场景内容逐帧移动。如图 1 所示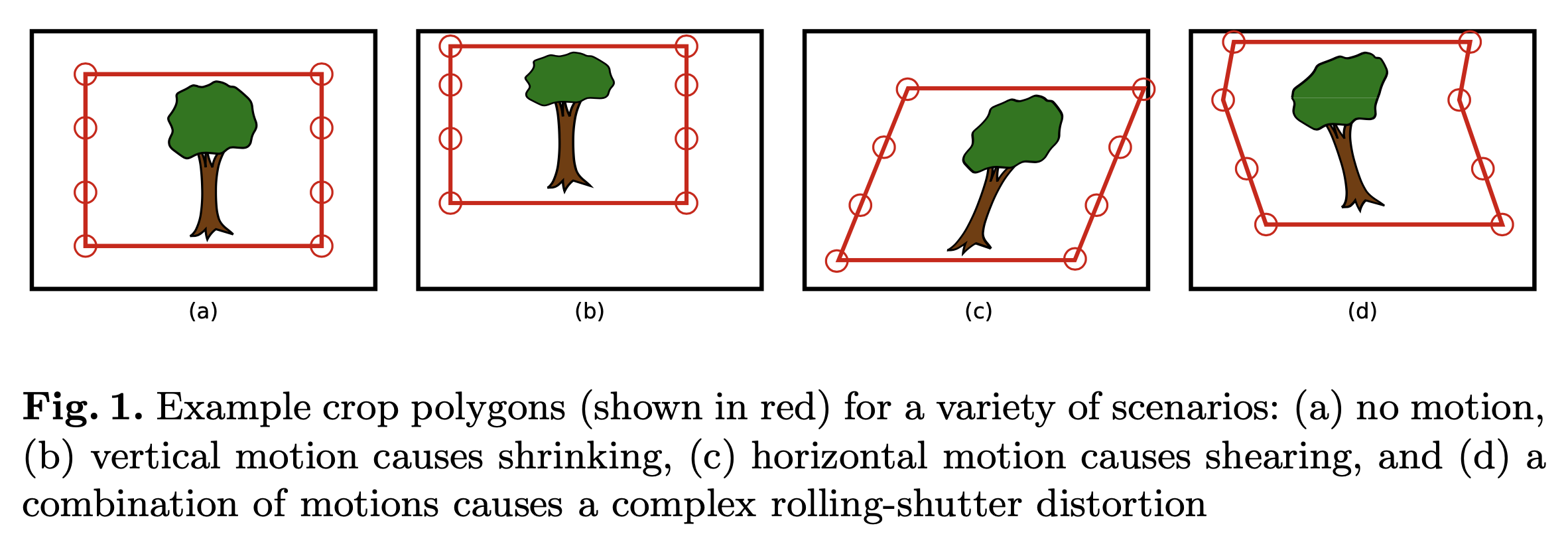

Camera Tracking Using the Gyroscope

我们将相机运动建模为全局坐标系中的旋转。陀螺仪提供了一系列带有时间戳的离散角速度测量值，我们将其积分以生成描述相机方向的时间函数。 理论上，我们还可以通过使用设备的加速度计测量平移来更精确，但实际上这很困难且价值有限。如果相机距离平面场景 3 米，那么 1 厘米平移引起的图像运动相当于旋转 0.19 度。 此外，平移的使用需要了解场景中物体的深度。

为了修复卷帘快门失真，我们需要知道特定行曝光时相机的方向。 给定帧 \(t_0\) 第一行的时间戳，第 r 行的时间戳为

\[ t_r = t_0 + \frac{r}{f_l}f_t \tag1 \]

其中 \(f_t\) 是总帧时间（即两个连续帧开始之间经过的时间），\(f_l\) 是图像行中的帧长度。 帧长是图像高度（以像素为单位）加上消隐行数的总和。 这两个值都取决于图像传感器和捕获模式，但我们假设它们在视频持续时间内是已知的并且是恒定的。如果这些值不是由传感器驱动提供的，也可以通过校准获得 [13, 14]。

我们可以通过计算其对应的行时间戳并从已知样本中插入相机方向来找到与图像中点 x 对应的设备方向。由于硬件和软件延迟，帧时间戳和陀螺仪时间戳之间存在小的偏移，我们假设这个偏移 \(t_d\) 是已知的，并且在捕获期间是恒定的。 在实践中，我们按照第 3.5 节中的详细说明校准此偏移量。

我们使用具有焦距 f 和投影中心 (cx, cy) 的投影相机模型；这三个参数定义了相机固有矩阵 K。这些参数使用 OpenCV 库进行离线校准。在已知 K 矩阵的情况下，滚动快门传感器在旋转运动下捕获的两个不同帧上的对应点\(x_1\)和\(x_2\)之间的关系为 :

\[ x_2 = KR_c(t_2)R_c^{-1}(t_1K^{-1})x_1 \tag2 \]

其中旋转矩阵 \(R_c\) 表示作为时间函数的相机坐标系中的相机方向，\(t_1\) 和 \(t_2\) 是点 \(x_1\) 和 \(x_2\) 的行时间戳。 我们可以将关于陀螺仪坐标系和时间原点的方程 2 重写为：

\[ x_2 = KTR_g(t_2 + t_d)R_g^{-1}(t_1 + t_d)T^{-1}K^{-1}x_1 \tag3 \]

其中 \(R_g\) 是从陀螺仪导出的方向，T 是相机和陀螺仪坐标系之间的转换，\(t_d\) 是上述陀螺仪和相机数据流之间的时间偏移。由于大多数移动设备都将陀螺仪和摄像头固定安装在一起，轴彼此平行，因此 T 只是一个置换矩阵。

Motion Model and Smoothing Algorithm

我们在每一帧用相机的方向和角速度参数化相机路径。我们用四元数\(p(k)\)和\(v(k)\)表示第 k 帧的物理和虚拟相机方向。 物理和虚拟角速度计算为从第 k 帧到第 k + 1 帧的离散角变化，并表示 \(p_∆(k)\)和\(v_∆(k)\)。由于帧速率是恒定的，因此这种速度表示中隐含了时间。对于每个新帧 k，我们的平滑算法使用来自最后一帧的虚拟参数以及来自最后一帧、当前帧和可选的未来小缓冲区的物理相机参数计算\(v(k)\)和\(v_Δ(k)\)帧（5 个或更少）。

我们的平滑算法创建了一个新的相机路径，当测量到的运动足够小以表明实际意图是保持相机静止时，该路径使虚拟相机保持静止，否则遵循测量运动的意图，角速度平滑变化 . 作为第一步，我们通过设置假设虚拟相机的新方向。 \[ \hat{v}^(k) = v(k − 1) · v_∆(k − 1) \tag4 \] 其中\(\cdot\)表示四元数积。简单地说，这个方程是通过从上次已知方向旋转相机，同时保持其角速度来计算新的相机方向。给定这个假设的相机方向 \(\hat{v}^(k)\)，我们使用等式 2 来计算生成的裁剪多边形的角坐标。在虚拟相机空间中，裁剪多边形是一个以图像中心为中心的固定矩形，但在物理相机空间中，它可能会发生倾斜或扭曲，并在帧内四处移动，如图 1 所示。裁剪多边形较小比输入大小，这在多边形边界和输入框架边缘之间留下了少量的 "padding"，如图 2 所示。我们将此填充分为两个同心区域，我们将其称为 "inner region"和 "outer region"。当假设的裁剪多边形位于图像的内部区域内时，我们断言假设 \(\hat{v}^(k)\)是好的，并使其成为当前的相机方向。在实践中，我们发现让运动在这种情况下衰减为零，这会使虚拟相机在可能的情况下偏向于保持静止。因此，如果裁剪多边形完全保留在内部区域内，我们将角度变化减少衰减因子 d，并将新的虚拟相机配置设置为：

\[ v_∆(k) = slerp(q_I; v_∆(k − 1); d) \tag5 \]

and

\[ v(k) = v(k − 1) · v_∆(k − 1) \tag6 \]

这里\(q_I\)代表恒等四元数，slerp 函数是两个四元数之间的球面线性插值 [17]。在我们的实现中，我们将混合权重设置为 d ≈ 0.95，这样每一帧的角度变化只会略微减少。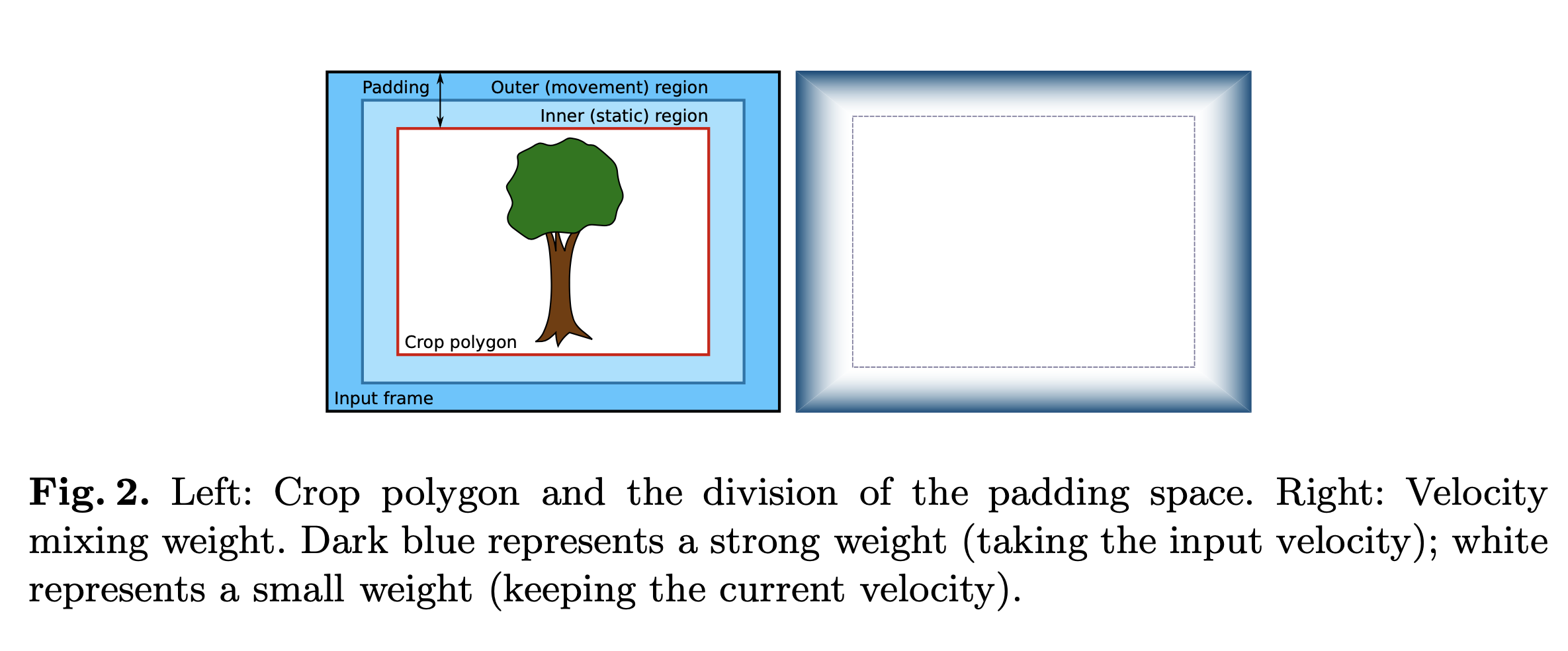

如果假设裁剪多边形的任何部分位于内部区域之外，我们将更新虚拟摄像机的角速度以使其更接近物理摄像机的变化率：

\[ v_∆(k) = slerp(p'_∆(k), v(k − 1), α) \tag7 \]

这里 \(p'_∆\) 是保持裁剪多边形从一帧到下一帧的相对位置的方向变化，计算为：

\[ p'_∆(k) = p(k) · p^∗(k − 1) · v(k − 1) \tag8 \]

其中\(p^∗\)表示反转旋转的四元数共轭。 该方程计算虚拟摄像机参考坐标系中从前一帧到当前帧的物理摄像机运动。 α项是一个混合权重，它是根据裁剪多边形和框架边缘之间剩余的填充量来选择的，如图 2 的右侧所示。直观地，如果裁剪多边形仅稍微超出内部 区域，α 应该接近 1，为当前速度分配更高的权重。 相反，如果假设的裁剪多边形靠近边缘（甚至外部），则 α 应为 0，这样输入速度匹配，裁剪多边形保持在相对于输入帧的相同位置。 我们用

\[ α = 1 − w^β \tag9 \] 其中 \(w \subseteq (0, 1]\) 是裁剪多边形超出内部区域的最大突出量，而 β 是决定响应锐度的指数。在裁剪多边形的任何角落在输入之外的极端情况下 帧，w 取值为 1，强制 α 为 0，并使虚拟摄像机跟上物理摄像机。

该算法运行良好，但当裁剪矩形突然碰到边缘时，它有时必须快速改变速度。 如果帧在处理之前可以在相机流水线中缓存一小段时间，那么可以检查更大的陀螺仪数据时间窗口，并且可以抢先避免急剧变化。 在本节的其余部分，我们扩展了我们的算法以使用来自前瞻缓冲区的数据来计算更平滑的路径。

我们可以通过将虚拟相机的方向及时向前投射并将其与“未来”时间的实际方向进行比较来跨越更大的帧窗口。让 a 是向前看的帧数，并假设：

\[ v(k + a) = v(k − 1) · v_∆(k)^{a+1} \tag{10} \]

然后，我们可以计算\(v_∆(k+a)\) 和 \(v(k+a)\)，就像我们在无前瞻情况下描述的那样。 如果裁剪多边形 a 帧到未来的投影在内部区域之外，我们可以更新\(v_∆(k)\) 为：

\[ v_∆(k) = slerp(v_∆(k + a); v_∆(k); γ) \tag{11} \]

其中 γ 是一个混合因子，它定义了我们应该将多少前瞻角度变化与当前角度变化混合。 使用接近 1 的 γ 值提供了在正确方向上的先发制人的推动，而不是硬约束。 请注意，我们不会在没有前瞻的情况下更新我们计算的虚拟摄像机位置，我们只会更新我们将用于下一帧的虚拟摄像机速度

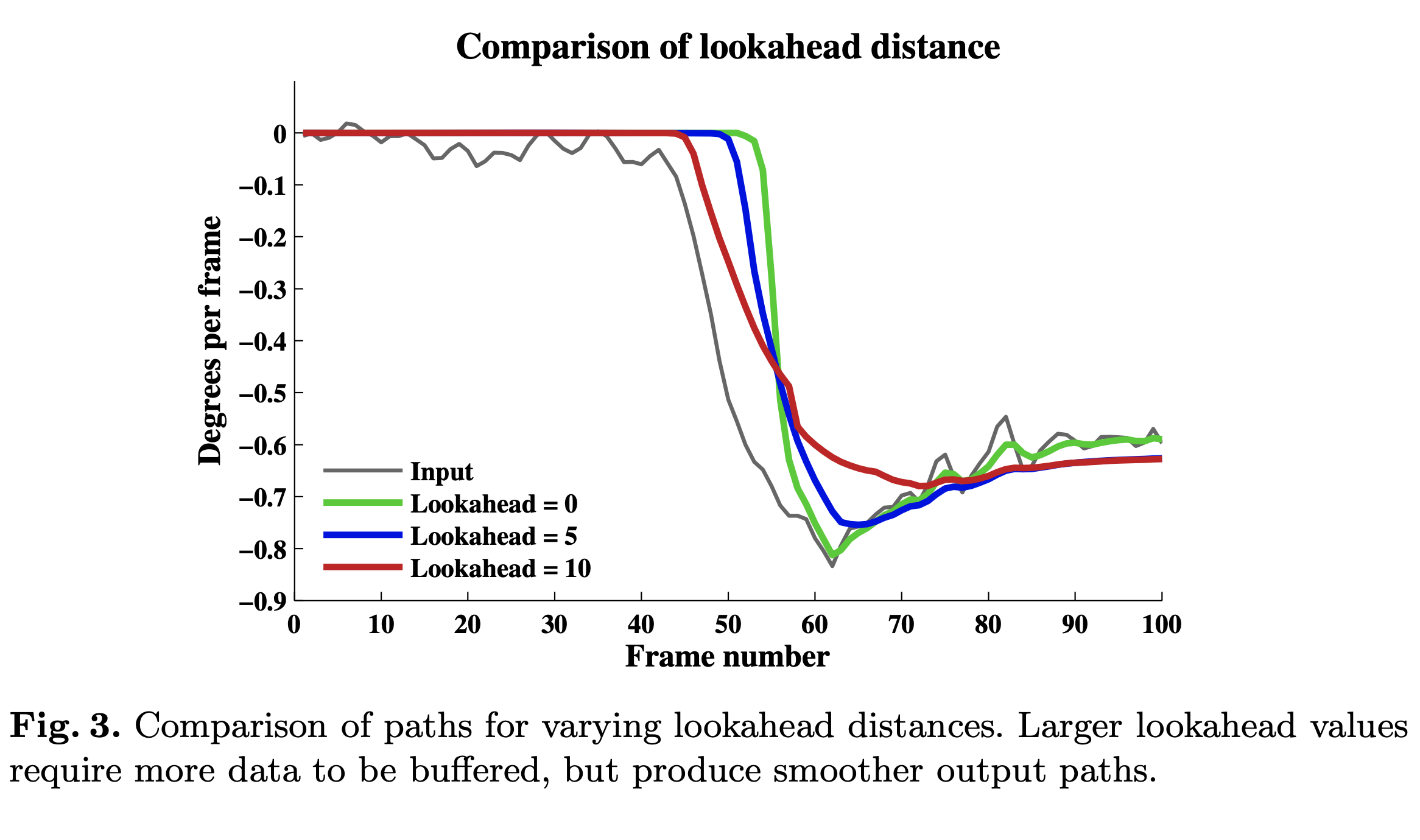
图 3 显示了一系列前瞻距离（以帧为单位）的路径比较。 较大的前瞻值会产生更平滑的路径，因为它们可以有效地“预测”较大的运动并轻轻地导致输出开始移动。但需要注意的是，我们的算法可以在没有前瞻的情况下工作并且仍然产生良好的结果。

Output Synthesis and Rolling-Shutter Correction

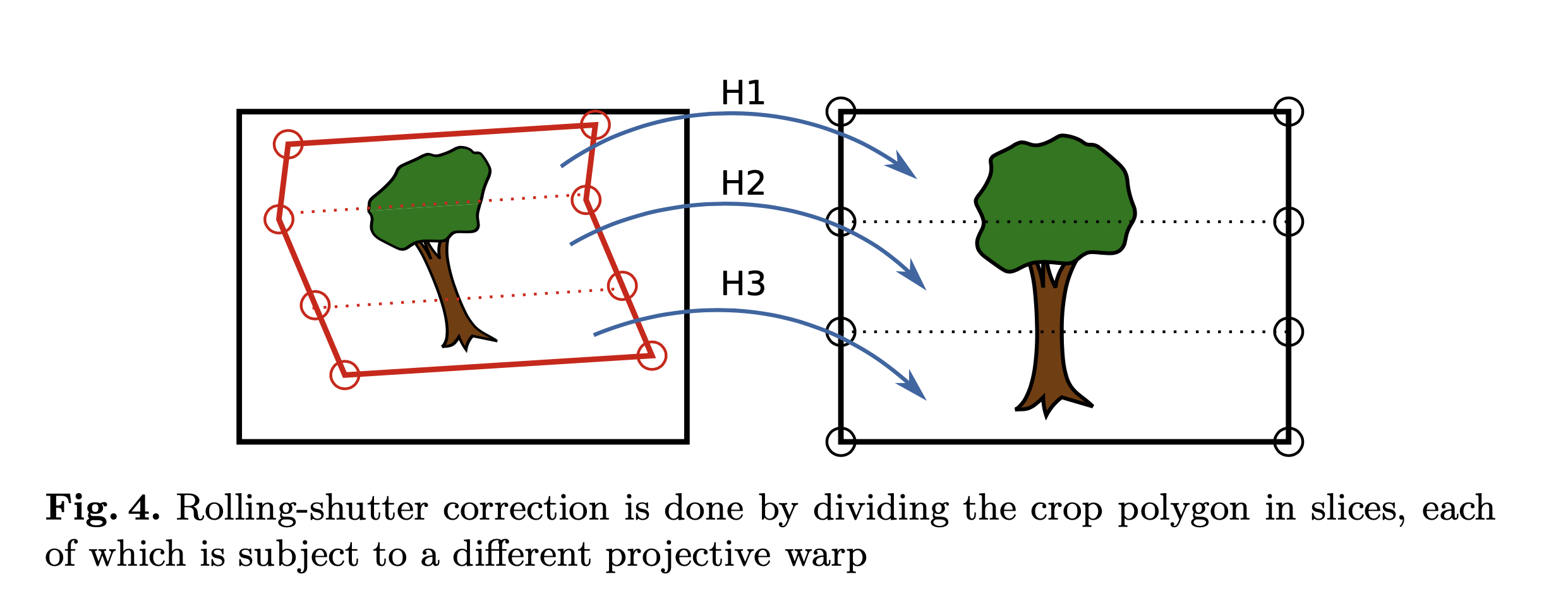
一旦我们计算了虚拟摄像机的新方向，我们就可以通过将裁剪多边形从视频输入投影到虚拟摄像机来合成输出。我们的裁剪多边形本质上是一个裁剪矩形，在垂直边缘上有多个拐点，如图 4 所示。拐点允许我们对多边形的每个切片使用不同的变换并修复滚动快门失真。对于每个切片，我们根据等式 2 计算单应矩阵。 我们将旋转矩阵 \(R_c(t2)\) 固定到虚拟输出相机的方向，并通过来自陀螺仪的数据计算 \(R_c(tk)\)，输入相机在每个拐点处的方向。我们将裁剪多边形的坐标设置为 OpenGL 着色器程序的纹理坐标，该程序将裁剪多边形从输入帧投影映射到虚拟相机。请注意，为了有效校正滚动快门效应，陀螺仪采样率应高于帧读出时间。在我们的实现中，我们以 200 Hz 的频率对陀螺仪进行采样，总共使用 10 个切片，或每个垂直边缘 9 个拐点。

Parameter Selection

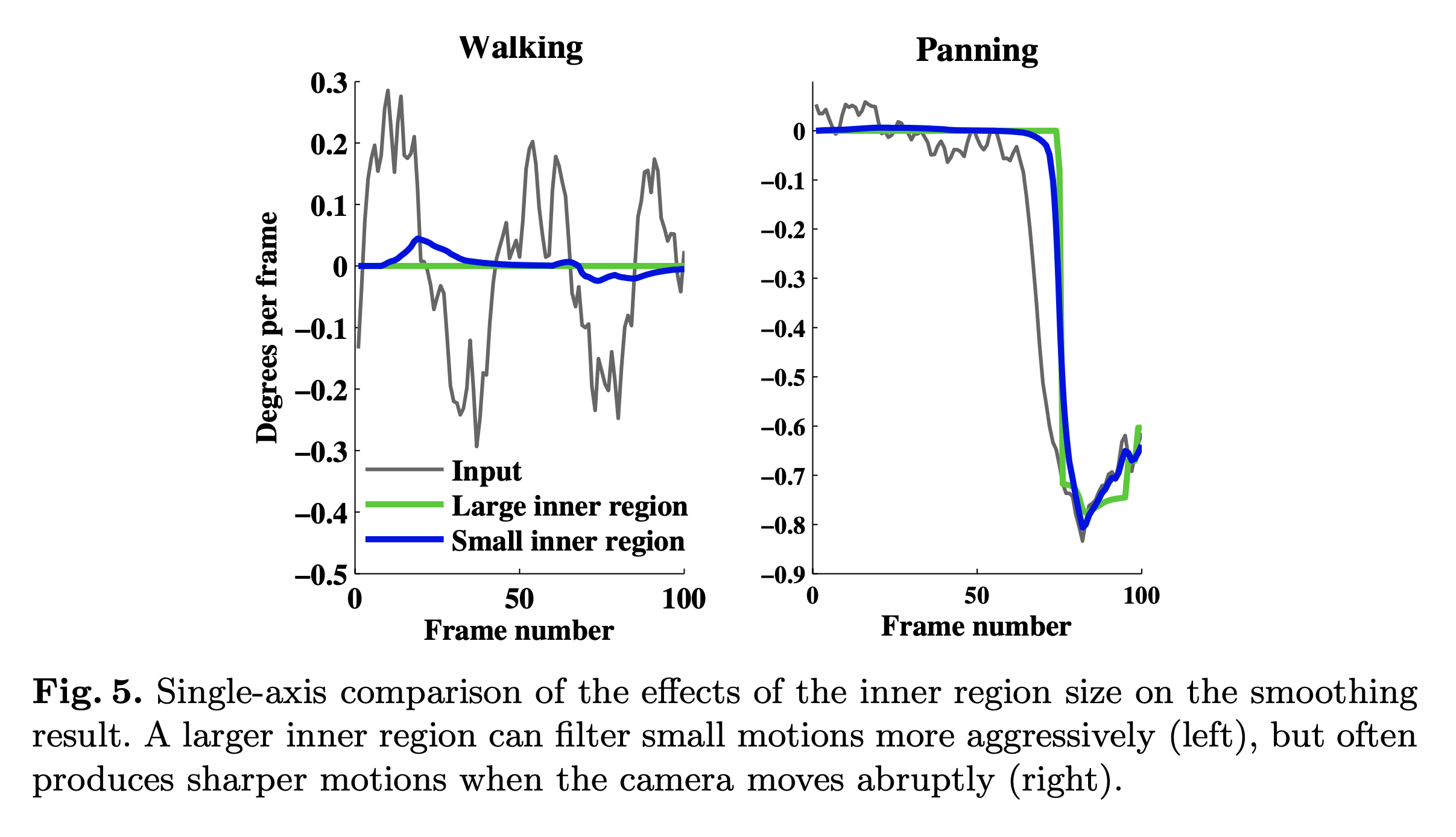
最重要的参数是输出裁剪多边形的大小以及分配给内部和外部区域的填充量。裁剪大小是平滑和图像质量之间的权衡：较大的裁剪多边形保留更多的输入图像，但留下较少的填充来平滑运动。填充分配是完全去除运动和剩余运动的平滑度之间的权衡。 如图 5 所示，较大的内部区域（绿色）能够使较大的运动（例如步行）变平，但当裁剪窗口接近框架边缘时必须更突然地移动。

Gyroscope and Camera Calibration

我们使用为此目的开发的校准程序来求解时间偏移 \(t_d\)。 我们在相机前面放置了一个校准图案，它由一个不对称的圆网格组成，然后我们在剧烈旋转相机的同时录制视频和陀螺仪读数。 即使存在运动模糊和滚动快门效果，也可以轻松地跨帧跟踪圆圈。 我们使用每个圆的质心作为特征点，并根据公式 3 通过最小化重投影误差的总和来迭代求解 \(t_d\)。通过在多个数据集上重复校准，我们确定偏移 \(t_d\) 几乎是恒定的。 我们还考虑了通过在捕获每一帧时跟踪关键点来进行在线校准的可能性 [18]，但事实证明离线方法足以满足我们的目的。

陀螺仪测量中任何静态偏移的积分将导致估计的方向缓慢偏离地面实况。然而，我们的稳定算法不受这种漂移的影响，因为它平滑了方向的相对变化。 我们在一到五帧的窗口内测量方向变化，在如此短的时间跨度内，积分漂移可以忽略不计。

Results

我们的源视频、结果和补充材料视频可在 https://research.nvidia.com/publication/non-linearfilter-gyroscope-based-video-stabilization 获得。

参考文献

< A Non-Linear Filter for Gyroscope-Based Video Stabilization >