ISP Raw 域之 BayerDemosaic

Bayer Demosaic 概述

RAW 域的最后一步处理是 Demosaic，将像素从 RAW 域变换到 RGB 域进行下一阶段的处理。Demosaic 算法的主要难点在于，RAW 域的任何一个像点（photosite）只包含一个真实的采样值，而构成像素（R,G,B）的其它两个值需要从周围像点中预测得到。既然是预测，就一定会发生预测不准的情况，这是不可避免的，而预测不准会带来多种负面影响，包括拉链效应（zipper artifacts），边缘模糊，颜色误差等。

所以 Demosaic 算法的主要挑战就是尽量提高算法的准确性，减少图像边缘损失和颜色误差。

Bayer 格式图像色彩恢复时有两种思路：

• 无方向性插值：不加边缘方向判断（思路：临近像素的均值），直接利用周围像素信息恢复。
• 有方向性插值：先判断边缘方向，再利用周围像素信息恢复。

Bayer 格式图像的绿色成分占比例较多，信息较丰富，色彩恢复时步骤通常是：a、先恢复 G 通道；b、再利用 G 通道信息恢复 R、B 通道。

CFA 双线性插值

无边缘检测

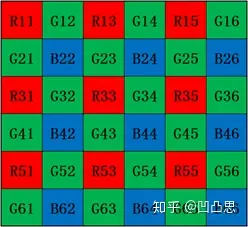
• 绿色像素上的 R，B 值分别由相邻的 2 个 R，B 像素的灰度求平均值得到。 以象素点 (2，3) 为例，即已知 G23 该点的 R，B 值计算公式如下： $$R_{23}=\frac{R_{13}+R_{33}}{2}$$ B_{23} = $$

• 红、蓝像素上的 G 值由相邻的 4 个绿色像素求平均值得到。 如图中象素点 (3，3) 和 (4，4)，即已知 R33 和 B44 这两点的绿色分量值表示为 $$G_{33}=\frac{G_{23}+G_{43}+G_{32}+G_{34}}{4}$$

  $$G_{44}=\frac{G_{34}+G_{54}+G_{43}+G_{45}}{4}$$

• 红色像素上的 B 值由对角线上相邻的 4 个 B 像素平均得到。象素点 (3，3) ，R33 的 B 值表示为。 $$B_{33}=\frac{B_{22}+B_{24}+B_{42}+B44}{4}$$ 蓝色像素上的 R 值由对角线上相邻的 4 个 R 像素平均得到。象素点 (4，4)，B44 的 R 值表示为 $$R_{44}=\frac{R_{33}+R_{35}+R_{53}+R_{55}}{4}$$

边缘检测，直接采用最近临同色像素的均值求解，图像边缘不够清晰，算法简单。

基于边缘检测和色差的 CFA 插值：Hibbard 原理

G 分量的恢复加入了相邻 G 通道的一阶微分方向判断因子。使用周围 G 通道值信息。

• 恢复采样点 R 和 B 点的绿色分量：例 B44。 梯度因子：水平方向 H $$\alpha =|G_{43}-G_{45}|$$ 竖直方向 W： $$\beta =|G_{34}-G_{54}|$$ 变化小的方向可能是边缘，所以 G44 表示如下： $$G_{44}=\frac{G_{43}+G_{45}}{2}(\alpha <\beta )$$ G_{44} = (> ) $$G_{44}=\frac{G_{34}+G_{54}+G_{43}+G_{45}}{4}(\alpha =\beta )$$

• 对 R、B 分量插值。基本思想是在图片的小平滑区域内，色差恒定的。假设像素点 P(i，j) 邻近的一个像素点是 P(m，n) 则有： $$\begin{gathered} R_{ij}-G_{ij}=R_{mn}-G_{mn} \\ {B}_{ij}-G_{ij}=B_{mn}-G_{mn} \end{gathered}$$ 例求 R 分量： 如已知 G43，红色分量表达式： $$R_{43}=\frac{R_{33}+R_{35}}{2}-\frac{G_{33}+G_{35}}{2}+G_{43}$$ 如已知 G34，红色分量表达式： $$R_{34}=\frac{R_{33}+R_{35}}{2}-\frac{G_{33}+G_{35}}{2}+G_{34}$$ 如已知 B44，红色分量表达式： $$R_{44}=\frac{R_{33}+R_{35}+R_{53}+R_{55}}{4}-\frac{G_{33}+G_{35}+G_{53}+G_{55}}{4}+G_{44}$$ 例求 B 分量：如已知 G43，蓝色分量表达式： $$B_{43}=\frac{B_{24}+B_{44}}{2}-\frac{G_{24}+G_{44}}{2}+G_{34}$$ 如已知 R33，蓝色分量表达式： $$B_{33}=\frac{B_{22}+B_{24}+B_{42}+B_{44}}{4}-\frac{G_{22}+G_{24}+G_{42}+G_{44}}{4}+G_{33}$$

G 通道有边缘检测采用相邻 G，恢复无色差、色度信息，R、B 通道无边缘检测，恢复采用色差信息。效果接近原始图，算法难度适中。

基于边缘检测和色差的 CFA 插值：laroche 原理

G 分量的恢复改用相邻 R 或 B 通道的二阶微分方向判断因子；恢复时使用相邻 G 通道信息。 R、B 分量的恢复同 Hibbard 使用色差原理。

• 恢复采样点 R 和 B 点的绿色分量：例 B44。 梯度因子：水平方向 H： $$\alpha =|2\ast B_{44}-B_{42}-B_{46}|$$ 竖直方向 W: $$\beta =|2\ast B_{44}-B_{24}-B_{64}|$$ 变化小的方向可能是边缘，所以 G44 表示如下： $$G_{44}=\frac{G_{43}+G_{45}}{2}(\alpha <\beta )$$

  $$G_{44}=\frac{G_{34}+G_{54}}{2}(\alpha >\beta )$$

  $$G_{44}=\frac{G_{34}+G_{54}+G43+G_{45}}{4}(\alpha =\beta )$$ 其他像素插值方法同 Hibbard。

G 通道有边缘检测采用相邻 B 色度信息，恢复用均值无色差信息、色度信息，R、B 通道无边缘检测，恢复采用色差信息。效果接近原始图，算法难度适中。

基于边缘、色度和色差自适应插值

G 分量的恢复改用相邻 R 或 B 的二阶微分加 G 通道的一阶微分方向判断因子；R、B 分量的恢复使用了色差原理。

• 恢复绿色分量 G。 已知 B44, 水平方向梯度和色度算子： $$\alpha =|2\ast B_{44}-B_{42}-B_{46}|+|G_{43}-G_{45}|$$ 已知 B44, 竖直方向梯度和色度算子： $$\beta =|2\ast B_{44}-B_{24}-B_{64}|+|G_{34}-G_{54}|$$ G 值公式： $$G_{44}=\{\begin{array}{ll}\frac{G_{43}+G_{45}}{2}+\frac{2\ast B_{44}-B_{42}-B_{46}}{4}& \alpha <\beta \\ \frac{G_{34}+G_{54}}{2}+\frac{2\ast B_{44}-B_{24}-B_{64}}{4}& \alpha >\beta \\ \frac{G_{34}+G_{43}+G_{45}+G_{54}}{4}+\frac{4\ast B_{44}-B_{24}-B_{42}-B_{46}-B_{64}}{8}& \alpha =\beta \end{array}$$ 已知 R33, 水平方向梯度和色度算子： $$\alpha =|2\ast R_{33}-R_{31}-R_{35}|+|G_{32}-G_{34}|$$ 已知 R33, 竖直方向梯度和色度算子： $$\beta =|2\ast R_{33}-R_{13}-R_{53}|+|G_{23}-G_{43}|$$ G 值公式： $$G_{33}=\{\begin{array}{ll}\frac{G_{32}+G_{34}}{2}+\frac{2\ast R_{33}-R_{31}-R_{35}}{4}& \alpha <\beta \\ \frac{G_{23}+G_{43}}{2}+\frac{2\ast R_{33}-R_{13}-R_{53}}{4}& \alpha >\beta \\ \frac{G_{32}+G_{34}+G_{23}+G_{43}}{4}+\frac{4\ast R_{33}-R_{31}-R_{35}-R_{13}-R_{53}}{8}& \alpha =\beta \end{array}$$

• 若已知 R33，求 B33。 B 分量的恢复采用相邻 G 的二阶微分加 B 通道的一阶微分方向判断因子；B 分量的恢复使用了色差原理 先求对角线方向的梯度和色度算子 $$\alpha =|2\ast G_{33}-G_{24}-G42|+\left|B_{24-B_{42}}\right|$$ = | 2 * G_{33} - G_{22} - G_{44} | + | B_{22} - B_{44} | $$B\mathrm{分}\mathrm{量}\mathrm{表}\mathrm{达}\mathrm{式}：$$ $$B_{33}=\{\begin{array}{ll}\frac{B_{24}+B_{42}}{2}-\frac{G_{24}+G_{42}}{2}+G_{33}& \alpha <\beta \\ \frac{B_{22}+B_{44}}{2}-\frac{G_{22}+G_{44}}{2}+G_{33}& \alpha >\beta \\ \frac{B_{22}+B_{24}+B_{42}+B_{44}}{4}-\frac{G_{22}+G_{24}+G_{42}+G_{44}}{4}+G_{33}& \alpha =\beta \end{array}$$ $$

• 已知 B44，求 R44。 先求对角线方向的梯度和色度算子 R 分量的恢复采用相邻 G 的二阶微分加 R 通道的一阶微分方向判断因子；R 分量的恢复使用了色差原理。 $$\alpha =|2\ast G_{44}-G_{35}-G53|+|R_{35}-R_{53}|$$ = | 2 * G_{44} - G_{33} - G_{55} | + | B_{33} - B_{55} | $$R\mathrm{分}\mathrm{量}\mathrm{表}\mathrm{达}\mathrm{式}：$$ $$B_{44}=\{\begin{array}{ll}\frac{R_{35}+R_{53}}{2}-\frac{G_{35}+G_{53}}{2}+G_{44}& \alpha <\beta \\ \frac{R_{33}+R_{55}}{2}-\frac{G_{35}+G_{55}}{2}+G_{44}& \alpha >\beta \\ \frac{R_{35}+R_{53}+R_{33}+R_{55}}{4}-\frac{G_{35}+G_{53}+G_{33}+G_{55}}{4}+G_{44}& \alpha =\beta \end{array}$$ $$

• 如已知 G43。 红色分量表达式： $$R_{43}=\frac{R_{33}+R_{53}}{2}-\frac{G_{33}+G_{53}}{2}+G_{43}$$ 蓝色分量表达式： $$B_{43}=\frac{B_{42}+B_{44}}{2}-\frac{G_{42}+G_{44}}{2}+G_{43}$$

• 如已知 G34。 红色分量表达式： $$R_{34}=\frac{R_{33}+R35}{2}-\frac{G_{33}+G_{35}}{2}+G_{34}$$ 蓝色分量表达式： $$B_{34}=\frac{B_{24}+B_{44}}{2}-\frac{G_{24}+G_{44}}{2}+G_{34}$$

R、G、B 通道分别进行了边缘检测，颜色恢复时采用了色差信息及其他通道的信息。效果接近原始图，算法难度较大。

基于边缘、色度和色差自适应插值之标志位：减少 False color

G 分量的恢复改用相邻 R 或 B 的二阶微分加 G 通道的一阶微分方向判断因子；并采用标志因子的统计，R、B 分量的恢复使用了色差原理。

• 对每个像素计算水平和垂直方向梯度和色度算子。
• 比较两个方向的算子大小，用 0 或 1 标记。
• 统计局部区域内如 3x3 窗口统计邻域九个位置的 flag 之和即 total_flag。
• 设置阈值，判断该像素在局部区域内最可能的方向。

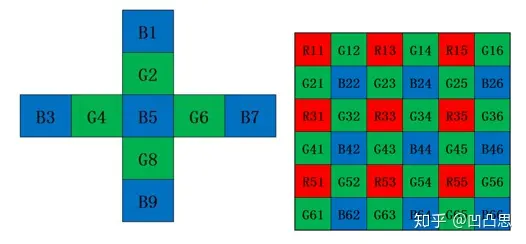
对于图 (a): 已知 B5 水平方向方向算子：

$$G_h=|G_4-G_6|+|2\ast B_5-B_3-B_7|$$

竖直方向方向算子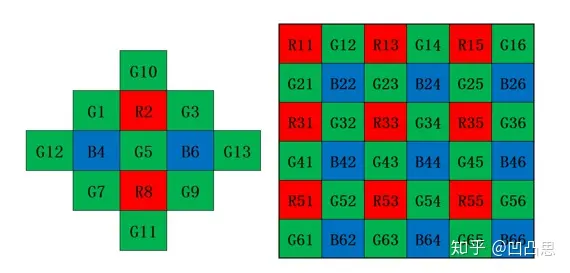： $$G_v=|G_2-G_8|+|2\ast B_5-B_1-B_9|$$ 方向梯度算子非固定 标志位： flag=1，$G_h<G_v$ ; flag=0，else

对于图 (b): 已知 G5（G43） 水平方向方向算子：

$$G_h=|2\ast G_5-G_{12}-G_{13}|+|G_1-G_3|+|G_7-G_9|$$

竖直方向方向算子： $$G_v=|2\ast G_5-G_{10}-G_{11}|+|G_1-G_7|+|G_3-G_9|$$

标志位： flag=1，Gh<Gv; flag=0，else 已知 G34 和 R33，flag 计算方法同理。

根据阈值判断方向的方法：

对于 B 和 R 位置，取 3x3 窗口，统计邻域九个位置的 flag 之和即 total_flag，在 [0.9] 之间，越大水平方向边界可能性越大，越小竖直方向为边界可能性越大。

取 high_thresh 和 low_thresh，判断边界方向。

total_flag > = high_thresh，水平方向存在边界，插值沿水平方向进行；

total_flag =< low_thresh，竖直方向存在边界，插值沿竖直方向进行；

low_thresh < total_flag < high_thresh，为平滑区域，插值在整个区域进行；

经验值， high_thresh 和 low_thresh 取 7 和 3.

插值方法同上。

有局部区域内边缘方向的整体判断，使得边缘方向判断更加准确。

CFA 插值，还有其他一些比较经典的算法：基于色比的算法；2003 年提出的 Lu 算法；基于权重的 CFA 插值算法；去 False color 的改进算法；其他一些在此基础上改进的算法等等

插值评价方法： 取一张 RGB 三色图像，按照 Bayer 格式取出对应的像素，构成 Bayer 格式图，然后经过 CFA 插值算法插值形成插值后图像。

评价参数：

• 颜色均方误差（CMSE）：插值前与插值后图像的对应像素间的差值（绝对值，方差值）之和的平均值。越小越重建接近原图，重建质量越高。

$$CMSE=\frac{1}{3HW}\sum _{k=R,G,B}\sum _{i=1}^H\sum _{j=1}^W{(I_o(i,j)k-I_d(i,j)k)}^2$$

• 例颜色峰值信噪比（Color Peak Signal to Noise Ratio ,CPSNR）：越大越重建接近原图，重建质量越高。

$$CPSNR=10lo{g}_{10}(\frac{{255}^2}{CMSE})$$

参考文献

https://zhuanlan.zhihu.com/p/98820927
https://zhuanlan.zhihu.com/p/40626620