ISP Raw 域之降噪

分类于 ， ， 阅读次数： Waline： 本文字数： 3.7k 阅读时长 ≈ 13 分钟

Raw 域降噪的原因

Sensor 本身的噪声

Sensor 输出的 RAW 图像本身是携带了噪声的，前面提到过 sensor 噪声的种类主要包括热噪声、光散粒噪声、读出噪声、固定模式噪声等。当 sensor 温度较高、增益较大、环境较暗的情况下各种噪声会变得更加明显，成为影响图像质量的主要因素。

LSC（Lens shading correction） 对噪声的影响

除了 Sensor 图像本身携带的噪声之外，图像每次会经过 ISP 模块的处理之后都会引入一些新的噪声，或者对原有噪声进行了放大。以 LSC 模块为例，LSC 校正的实质是在输入图像上乘以一个与像素位置有关的增益系数以补偿光信号的衰减，而补偿的规律是越远离图像中心的地方增益越大。由于 ISP 所用乘法器的精度是有限的，每做一次乘法就会重新引入一次截断误差，这是新增的噪声来源，所以经 LSC 处理后图像的整体噪声水平会有所增加，而且在图像的边缘处表现会更加明显，典型的效果如下图所示。

Shading 固然是不好的，需要校正，但是为了校正 shading 而给图像引入噪声同样也不好的，所以人们需要权衡在多大程度上校正 shading 能够收到满意的效果。这是在主观图像质量调试阶段需要考虑的问题之一。

最后

噪声在 ISP 流水线各模块中会不断产生、传播、放大、改变统计特性，对图像质量的影响会越来越大，而且越来越不容易控制。因此处理噪声的基本原则是越早越好，随时产生随时处理，尽可能将问题消灭在萌芽状态。目前主流的 ISP 产品中一般会选择在 RAW 域、RGB 域、YUV 域等多个环节设置降噪模块以控制不同类型和特性的噪声。在 YUV 域降噪的方法已经得到了广泛的研究并且出现了很多非常有效的算法，但是在 RAW 域进行降噪则因为 RAW 数据本身的一些特点而受到不少限制。主要的限制是 RAW 图像中相邻的像素点分别隶属于不同的颜色通道，所以相邻像素之间的相关性较弱，不具备传统意义上的像素平滑性，所以很多基于灰度图像的降噪算法都不能直接使用。又因为 RAW 数据每个像素点只含有一个颜色通道的信息，所以很多针对彩色图像的降噪算法也不适用。

频域滤波器

意法半导体的算法专家们提出了一种基于频域变换的方法，基本思想是将使用 8x8 大小的 DCT 变换将小块图像变换到频域，然后对频率分量进行分析：

  • 如果 DCT 变换后非零系数很少，且能量集中在低频，说明是平坦区域，应加强降噪力度。
  • 如果两个相邻的 DCT 单元具备相同或相近的直流分量，则说明是平坦区域，应加强降噪力度。
  • 如果某个方向（水平、垂直、对角）上存在明显占优的系数，则说明存在强边缘，应避免降噪。
  • 如果某两个方向上存在占优的系数，则说明存在弱边缘，应进行中等强度的降噪。
  • 如果很多方向上都有非零的系数，但又没有明显的优势系数，此时可能是纹理与噪声并存的情况，需要一定强度的滤波，削弱高频成分。

详细可参考 https://www.researchgate.net/publication/220539137_Chroma_Noise_Reduction_in_DCT_Domain_Using_Soft-Thresholding

空域滤波器（Spatial Filter）

空域降噪是一种 2D 降噪方法，它只处理一帧图像内部的噪声，主要方法是使用空域滤波器对图像进行滤波。滤波操作通常是针对以某个像素为中心的滤波窗口上进行的，滤波窗口的大小与具体的算法有关，常用的大小有 3x3、5x5、7x7 等尺寸。滤波操作在数学上称为卷积，需要使用一个与滤波窗口大小一致的卷积核，卷积核的每个元素代表一个权重，与对应位置的图像像素值相乘，然后所有乘积累加到一起就是滤波后的结果。

卷积滤波用公式表示是，

\[ g(x,y) = \sum_{s=-a}^{a}\sum_{t=-b}^{b}w(s,t)f(x+s,y+t) \]

下面是卷积滤波操作的示意图。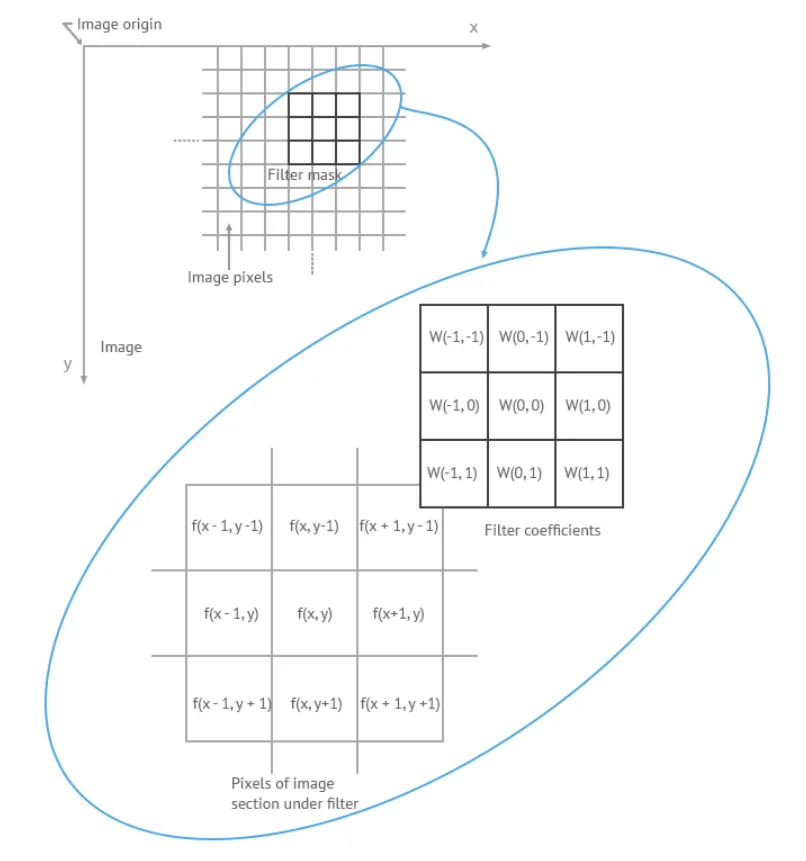

  • 经典低通滤波器，如均值滤波、中值滤波、高斯滤波、维纳滤波等。这类方法的优点是比较简单，占用资源少，速度快，缺点是滤波器是各向同性的，容易破坏图像中的边缘。另外由于没有考虑颜色通道之间的相关性所以也容易引入伪彩等噪声，而人眼对这种颜色噪声是比较敏感的。
  • 改进的经典滤波器，如 Eplison 滤波、双边滤波 (bilateral filter)，在经典滤波器的基础上增加了阈值检测用于区分同类像素和异类像素，同类像素分配较大的滤波权重，异类像素则权重很小因而基本不参与滤波。这类方法的优点是可以有效地保护图像边缘，复杂度增加也不大，其它特点与经典滤波器基本相同。

时域降噪（Temporal）

时域降噪是一种 3D 降噪方法，它的主要思想是利用多帧图像在时间上的相关性实现降噪。

一种最简单的实现方法是时域均值滤波，即将相邻几帧图像做加权平均。由于累加后噪声的增长速度（根号关系）小于信号的增长速度（线性关系），所以图像的信噪比会提高。这种方法的主要问题在于只适合处理静态图像，如果画面中存在运动的物体则会出现伪影（ghost effect）。

运动适应降噪 Motion Adaptive Noise Filter

对基本的时域降噪进行一些改造就可以得到一种自适应降噪算法。假设图像中坐标 (x,y) 处的像素值为 P(x,y)， 新一帧中同位置像素值为 P'(x,y)，如果两个像素值的差异小于某阈值，即|P'-P|<threshold， 则可以用 P 代替 P'。这种方法对静止的图像效果非常明显。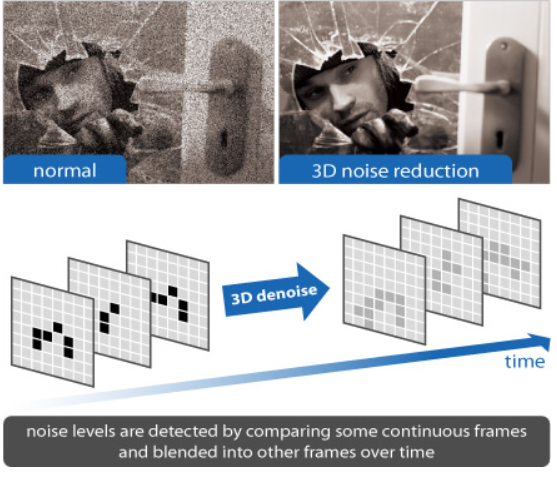

假设 \(\hat{g}(i,j,k)\) 代表有噪声的视频信号序列，其中 (i,j) 代表像素坐标，k 代表时间序列，则 \(\hat{g}(i,j,k)\) 可以表示为真实信号 \(\hat{f} (i,j,k)\) 和噪声信号 \(\hat{n} (i,j,k)\) 的叠加形式：

\[ \hat{g}(i,j,k) = \hat{f}(i,j,k) + \hat{n}(i,j,k) \]

真实信号 f (i,j,k) 当然是不可能知道的，只能用某种方法对其进行估计。一种经典的估计方法是采用以下非线性滤波器：

\[ \hat{f} (k) = \hat{f}(k-1) + \alpha [\hat{g}(k) - \hat{f}(k-1)] \]

其中 \(\hat{f}(k)\) 代表第 k 帧图像，它的来源是在第 k-1 帧图像的基础上叠加了 g(k) 与 \(\hat{f}(k-1)\) 的差值成分，即 \(∆= α(k)|\hat{g}(k)-\hat{f}(k-1)|\) ，其中α(k) 是与∆相关联的阻尼系数。

  • 当∆ < thres0 时判断为噪声，采用α(k)=0。
  • 当∆ > thres1 时判断为真实信号，采用取α(k)=1。
  • 当 thres0 < ∆ < thres1 时α(k) 介于 0 和 1 之间。

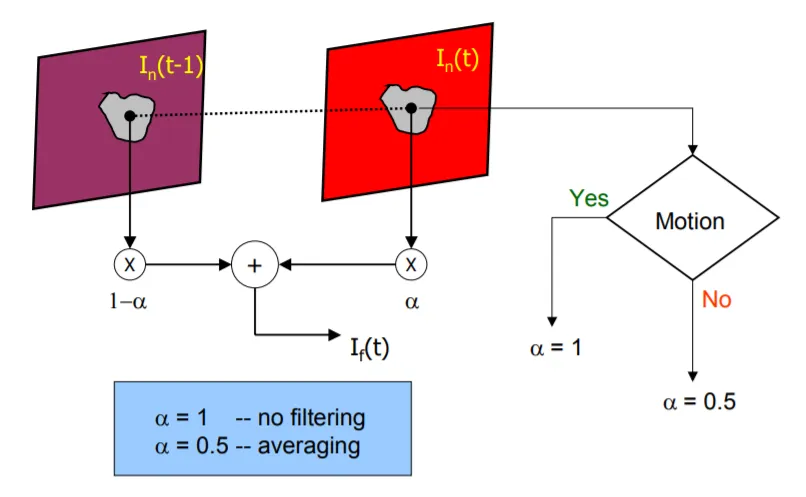
当然，这种方法的局限也是很明显的，一方面阈值的选取需要能够有效地区分噪声与画面变化，这本身不是一件很容易的事情；另一方面当像素变化超过阈值后此方法就失效了，因此画面前景部分的噪声处于逍遥法外的状态，这也是一个问题。

因此，一个理想的滤波器应该同时满足几个特征，即

  • 能够有效地区分画面的前景（运动目标）和背景（不动目标）。
  • 对画面中的前景像素进行空域降噪。
  • 对画面中的背景像素进行时域降噪。

空域时域降噪（STNR）

STNR 是一种 2D+3D 降噪方法，它通过一套算法判别一个像素是属于前景还是背景，被判决为背景的像素将会参与时域平滑，被判决为前景的像素将会参与空域平滑，而判决条件则每一帧都在动态更新，以尽可能保证判决准确性。

光流法 Optical Flow

假设前一帧时间为 t， 后一帧时间为 t+δt。在理想情况下（δt 很小，在δt 时间内图像亮度保持稳定，物体运动速度不大，并且不会突然消失或被遮挡），则前一帧 I 的像素点 I(x, y, z, t) 在后一帧中的位置为 I(x+δx, y+δy, z+δz, t+δt )。

如果假定图像亮度恒定，即可得到光流法的约束方程（constraint equation）

\[ I(x,y,z,t) = I(x+δx, y+δy, z+δz, t+δt ) \]

进一步假定图像中的物体运动速度不大，则后一帧图像可以用前一帧图像的泰勒展开形式表示（只保留一阶近似）

\[ I(x+δx, y+δy, z+δz, t+δt ) = I(x,y,z,t) + \frac{\mathrm{d} I}{\mathrm{d} x} δx + \frac{\mathrm{d} I}{\mathrm{d} y} δy + \frac{\mathrm{d} I}{\mathrm{d} z} δz + \frac{\mathrm{d} I}{\mathrm{d} t} δt \]

根据约束方程，上式中偏导数之和应为 0，即

\[ \frac{\mathrm{d} I}{\mathrm{d} x} V_x + \frac{\mathrm{d} I}{\mathrm{d} y} V_y + \frac{\mathrm{d} I}{\mathrm{d} z} V_z + \frac{\mathrm{d} I}{\mathrm{d} t} V_t = 0 \]

对于二维图像可忽略 z 分量，约束方程的最终形式为：

\[ I_x V_x + I_y V_y = - I_t \]

通常在一个小窗口内进行光流计算，采用最小二乘法求得该窗口内的平均运动向量。理想情况下，小窗口内的像素应具有一致的运动向量，因此求得的平均向量就代表着物体真实的运动方向。

块匹配法 Block Matching

块匹配的思想是在参考帧（通常是上一帧）中的一个小范围内搜索与当前块 (block) 最匹配的块，如果确实能够找到则计算出运动向量 v。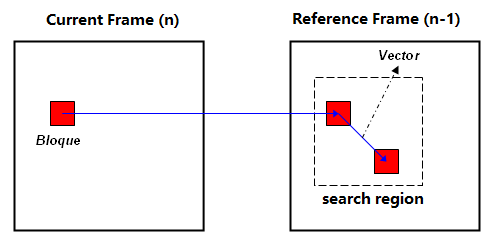

所谓“最匹配”的块其实可以有很多种不同的评判标准。常用的标准有 Mean Squared Error (MSE) 以及 Mean Absolute Error (MAE) 等算法。

搜索区域一般是根据产品的需求和设计约束而定，常用的有 13x13，17x17 像素等。搜索区域越大能够检测的运动速度越大，但是所需的算力成本也会呈平方增长。

当图像种存在重复的纹理模式时，光流法和块匹配法都容易失效。在下图的例子中，绿框所示的块状纹理和黄框所示的边缘纹理都容易引起算法失效。而蓝框所示的含直角的块则较容易被算法正确识别。

BM3D 算法

基础估计

  • 对于每个目标图块，在附近寻找最多 MAXN1（超参数）个相似的图块，为了避免噪点的影响，将图块经过 2D 变换（代码中使用 DCT 变换）后再用欧氏距离衡量相似程度。按距离从小到大排序后取最多前 MAXN1 个。叠成一个三维数组。

\[ \begin{equation} d\left(Z_{x_R}, Z_x\right)=\frac{\left\|\Upsilon^{\prime}\left(\mathcal{T}_{2 \mathrm{D}}^{\mathrm{ht}}\left(Z_{x_R}\right)\right)-\Upsilon^{\prime}\left(\mathcal{T}_{2 \mathrm{D}}^{\mathrm{ht}}\left(Z_x\right)\right)\right\|_2^2}{\left(N_1^{\mathrm{ht}}\right)^2} \end{equation} \]

  • 对 3D 数组的第三维，即图块叠起来后，每个图块同一个位置的像素点构成的数组，进行 DCT 变换后，采用硬阈值的方式将小于超参数 \(\lambda_{3D}\) 的成分置为 0。同时统计非零成分的数量作为后续权重的参考。后将第三维进行逆变换。

\[ \begin{equation} \widehat{\mathbf{Y}}_{S_{x_R}^{\mathrm{ht}}}^{\mathrm{ht}}=\mathcal{T}_{3 \mathrm{D}}^{\mathrm{ht}^{-1}}\left(\Upsilon\left(\mathcal{T}_{3 \mathrm{D}}^{\mathrm{ht}}\left(\mathbf{Z}_{S_{x_R}^{\mathrm{ht}}}\right)\right)\right), \end{equation} \]

  • 将这些图块逆变换后放回原位，利用非零成分数量统计叠加权重，最后将叠放后的图除以每个点的权重就得到基础估计的图像，此时图像的噪点得到了较大的去除。

\[ \begin{equation} \hat{y}^{\text {basic }}(x)=\frac{\sum_{x_R \in X} \sum_{x_m \in S_{x_R}^{\mathrm{ht}}} w_{x_R}^{\mathrm{ht}} \widehat{Y}_{x_m}^{\mathrm{ht}, x_R}(x)}{\sum_{x_R \in X} \sum_{x_m \in S_{x_R}^{\mathrm{ht}}} w_{x_R}^{\mathrm{ht}} \chi_{x_m}(x)}, \forall x \in X, \end{equation} \]

最终估计

  • 由于基础估计极大地消除了噪点，对于含噪原图的每个目标图块，可以直接用对应基础估计图块的欧氏距离衡量相似程度。按距离从小到大排序后取最多前 MAXN1 个。将基础估计图块、含噪原图图块分别叠成两个三维数组。

\[ \begin{equation} S_{x_R}^{\text {wie }}=\left\{x \in X: \frac{\left\|\widehat{Y}_{x_R}^{\text {basic }}-\widehat{Y}_x^{\text {basic }}\right\|_2^2}{\left(N_1^{\text {wie }}\right)^2}<\tau_{\text {match }}^{\text {wie }}\right\} . \end{equation} \]

  • 对含基础估计 3D 数组的第三维，即图块叠起来后，每个图块同一个位置的像素点构成的数组，进行 DCT 变换，利用如下公式得到系数。

\[ \begin{equation} \mathbf{W}_{S_{x_R}^{\text {wie }}}=\frac{\left|\mathcal{T}_{3 \mathrm{D}}^{\text {wie }}\left(\widehat{\mathbf{Y}}_{S_{x_R}^{\text {waic }}}^{\text {wasic }}\right)\right|^2}{\left|\mathcal{T}_{3 \mathrm{D}}^{\text {wie }}\left(\widehat{\mathbf{Y}}_{S_{x_R}^{\text {basic }}}^{\text {baic }}\right)\right|^2+\sigma^2} \end{equation} \]

  • 将系数与含噪 3D 图块相乘放回原处，最后做加权平均调整即可得到最终估计图。相对于基础估计图，还原了更多原图的细节。

\[ \begin{equation} \widehat{\mathbf{Y}}_{S_{x_R}^{\text {wie }}}^{\text {wie }}=\mathcal{T}_{3 \mathrm{D}}^{\text {wie }^{-1}}\left(\mathbf{W}_{S_{x_R}^{\text {wie }}} \mathcal{T}_{3 \mathrm{D}}^{\text {wie }}\left(\mathbf{Z}_{S_{x_R}^{\text {wie }}}\right)\right) \end{equation} \]

BM3D 代码实现

  • BM3D 官网，Matlab 实现 https://webpages.tuni.fi/foi/GCF-BM3D/。
  • 一篇 BM3D 的快速实现，提供了源码 https://www.ipol.im/pub/art/2012/l-bm3d/。

参考文献

https://zhuanlan.zhihu.com/p/98820927
https://zhuanlan.zhihu.com/p/536544215
https://zhuanlan.zhihu.com/p/46399784
https://www.ipol.im/pub/art/2012/l-bm3d/
https://webpages.tuni.fi/foi/GCF-BM3D/
https://zhuanlan.zhihu.com/p/102423615