ISP YUV 域之 CE(Contrast Enhancement)
相关概念
直方图 Histogram
在分析图像数据的统计特性时,有时可以抛弃图像的色度分量,只考察图像的亮度分量,此时可以引入图像的亮度直方图(Luminance Histogram),以常用的 8 位精度图像为例,直方图的 X 轴为 0~255,共 256 个桶,每个桶刚好覆盖 1 个像素值,直方图的 Y 轴表示每个桶盛纳了多少个像素。所有桶中盛纳的像素数加到一起应等于图像的总像素数。
在分析画面的亮暗特征,人们经常把亮度区间定性地划分成暗调、阴影、中调、亮调、高光等几个区域,各区域的边界则可以根据应用特点灵活掌握。

当需要分析图像的颜色特性时,可以引入通道直方图(Channel
Histogram),分别对 R/G/B 三个颜色通道进行直方图统计。 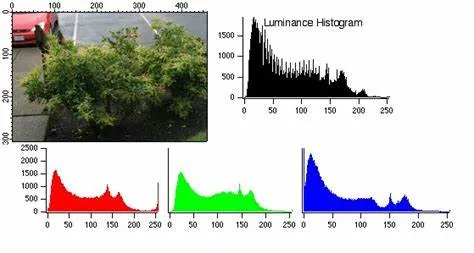
对比度 Contrast
图像对比度指的是一幅图像中最亮的白和最暗的黑之间灰度反差的大小。差异越大代表对比越大,否则对比越小。一种常用的定量度量方法是 Michelson 对比度,定义为
\[ C_M = \frac{I_{Max} - I_{Min}}{I_{Max} + I_{Min}} \]
当一幅图像最白和最黑像素灰度都是 128 时,图像对比度最低,C=0。 当一幅图像最白像素灰度=255,最黑像素灰度=0 时,图像对比度最高,C=1.0。
对比度拉伸 Contrast Stretching
既然搞清楚了图像不通透的原因,就很容通过数学的方法将一个低对比度图像处理得更通透一些。一类简单有效的处理方法叫做对比度拉伸(Contrast
Stretching),基本思想是用一个下图所示分段线性函数(Piece-Wise Linear,
PWL Function)对像素亮度进行映射。 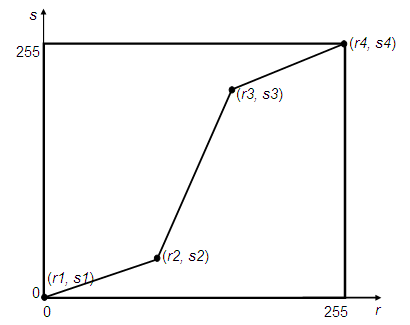
这种方法虽然简单,但是对很多低对比度图像能够收到相当好的效果。 
对比度拉伸的局限:对比度拉伸适合处理低动态(LDR)图像,这类图像的特点是对比度低,直方图的跨度较小,存在向两极拉伸的空间。对于高动态(HDR)图像,直方图跨度已经很大,对比度拉伸没有操作的空间。
直方图均衡化 Histogram Equalization
直方图均衡化被认为是提升图像对比度最为有效的方法,它的基本思想是用数学方法重新调整像素的亮度分布,使调整后的直方图具有最大的动态范围,每个桶(bin/bucket)盛纳的像素数量几乎相等。
用数学语言描述,假设均衡前直方图的像素密度函数为 p(x),每个桶的宽度为 dx,则每个桶的像素数量为 p(x)dx。假设均衡后像素密度函数为 p(y),且 p(y) 为常数,不妨取 1。
直方图均衡的方法是 dy=p(x)dx,意义是将源直方图 dx 宽度所盛纳的 p(x)dx
个像素映射到目标直方图的 dy
宽度中,映射前后像素数量不变,密度发生变化,意义如下图所示。 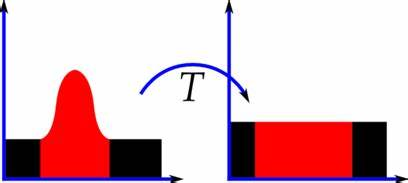
显然直方图均衡前后图像的总像素数量应保持不变,所以有约束方程
\[ \int_{0}^{1} p(x)dx = \int_{0}^{1} dy = 1 \]
我们的最终目标是求解 x 与 y 的映射函数 y=f(x),这个的问题并不困难,
\[ y = f(x) = \int_{0}^{x}p(u)du = P(x) - P(0) = P(x) \]
这个公式可以理解为,x 对应的 y 值是原图上 0~x
这些像素的概率之和。原图中最大的 x 对应 y=1。 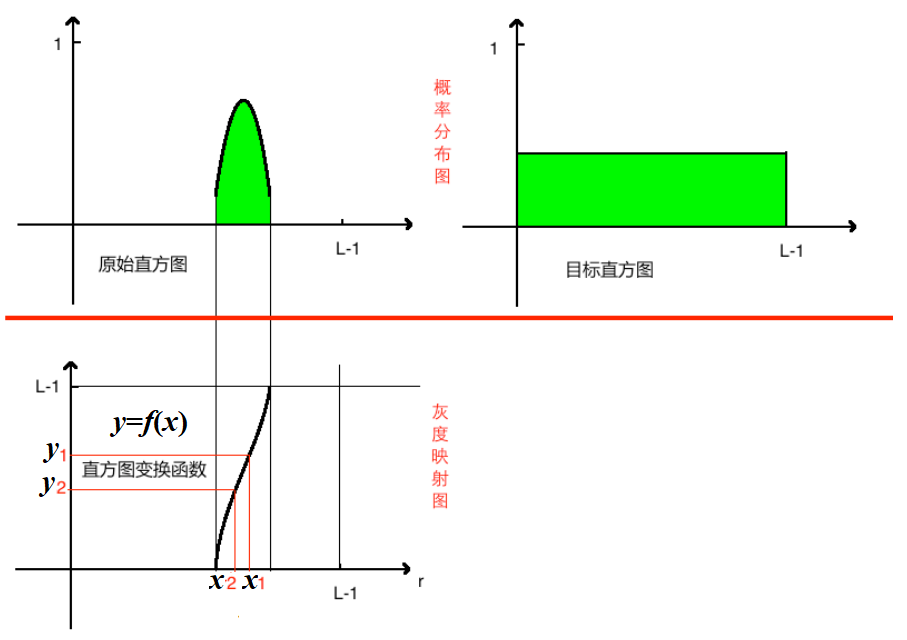
下面一组图显示了直方图均衡改善图像对比度的效果。 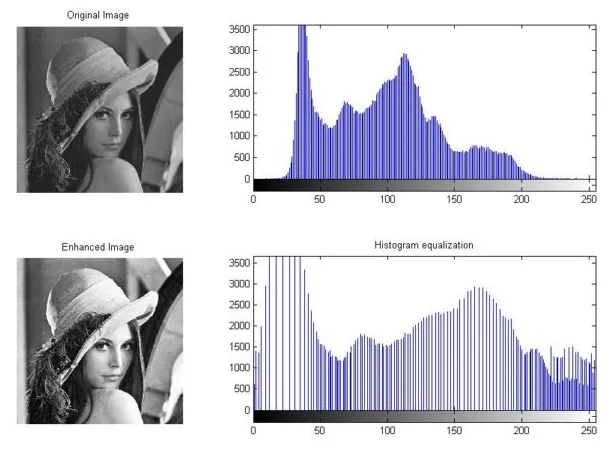
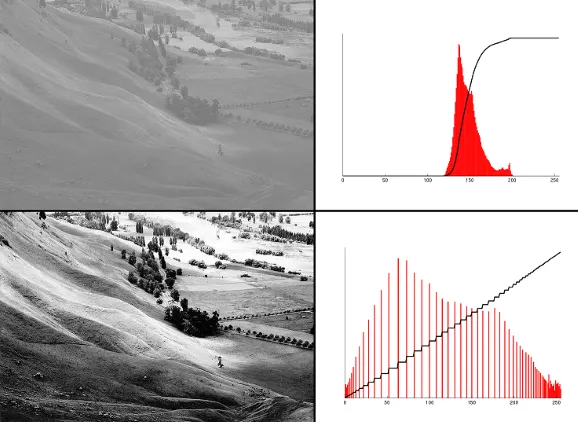
下图是对直方图拉伸和均衡两种方法的效果做比较。 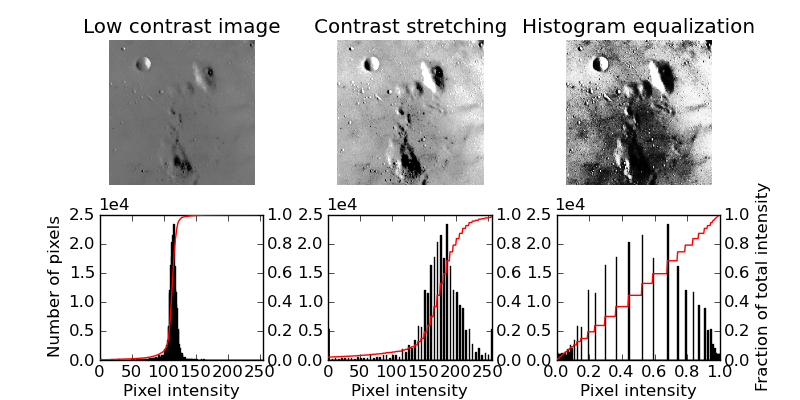
直方图均衡的局限
朴素的直方图均衡算法对整幅图像的像素使用相同的变换公式,当图像像素值分布比较均衡时效果较好。如果图像的颜色比较集中,比如存在明显的暗区或亮区,则这些区域的处理效果会不太理想。
分色问题
当原图的直方图比较集中时,这意味着原图实际上只出现了少数几个颜色值,如果对原图进行拉伸操作,则这些颜色之间的距离就会变大,直方图上留下了更多概率为
0
的空洞,这样,原本比较接近的颜色在拉伸后的图上会出现显著的差异,图像出现颜色分层现象(banding),或者叫分色现象。

对齐问题
直方图均衡的一个重要特征是把原图中最亮的像素对齐到预设的最大值(比如 8bit 图是 255)。当原图中颜色比较丰富时,这个操作一般问题不大。但是也会有有一些比较极端的情况,比如原图中所有像素都是一个值(例如 8,这对应一幅纯黑的图像,多半是拍摄于夜间),则均衡之后所有像素都被映射到 255,图像变成了纯白的。于是,直方图均衡相当于无脑改变了原图的色调,而不管这种改变是否合理。
噪声问题
直方图均衡算法一种常见的问题是放大暗区的噪声,其根源也是对齐问题。如果一个区域的像素分布大体是均匀的,但是图像中带有一些噪声,则
HE 变换函数会把原图中很窄的 x 值分布映射到整个 y
值空间,这同时也就放大了原图中的噪声。 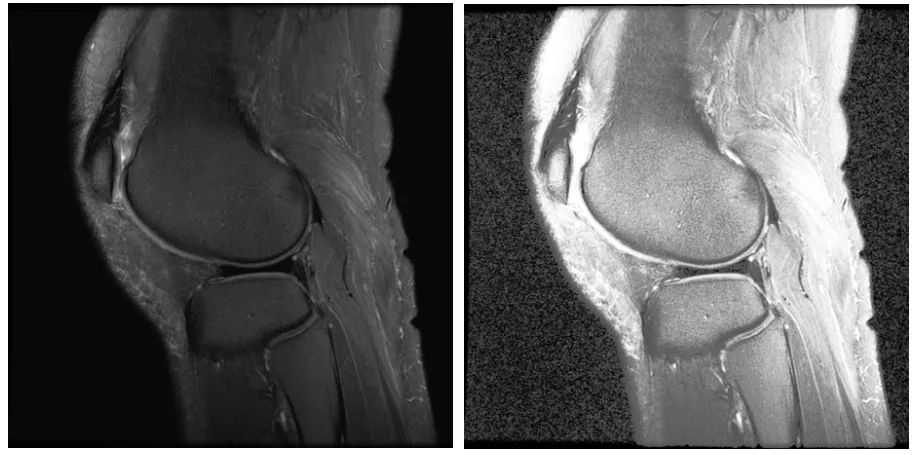
自适应直方图均衡 Adaptive Histogram Equalization(AHE)
参考人类视觉的局部性原理,人们提出了自适应直方图均衡算法(AHE),基本思想是将图像分成若干个区域(tile),比如 8x8=64 个 tile,直方图均衡的基本单位不再是整个图像,而是对每个小区域做直方图均衡。AHE 更适合于用来改善图像的局部对比度,以及增强图像边缘信息,但是并没有解决直方图均衡会放大图像噪声的问题。
限制对比度自适应直方图均衡 CLAHE
我们已经知道,如果原图中某些颜色的频率太高,挤占了其它颜色的机会,均衡后的图像就会出现颜色分层、色调异常、噪声过大等比较棘手的问题。
为了解决这些问题,一个显然的思路就是损有余而补不足,或者叫削峰填谷,把我们认为多余的概率平均分摊给其它像素,使亮度增益相对均匀地散布到所有像素上,而不是让某一个颜色突然地对齐到最大亮度。
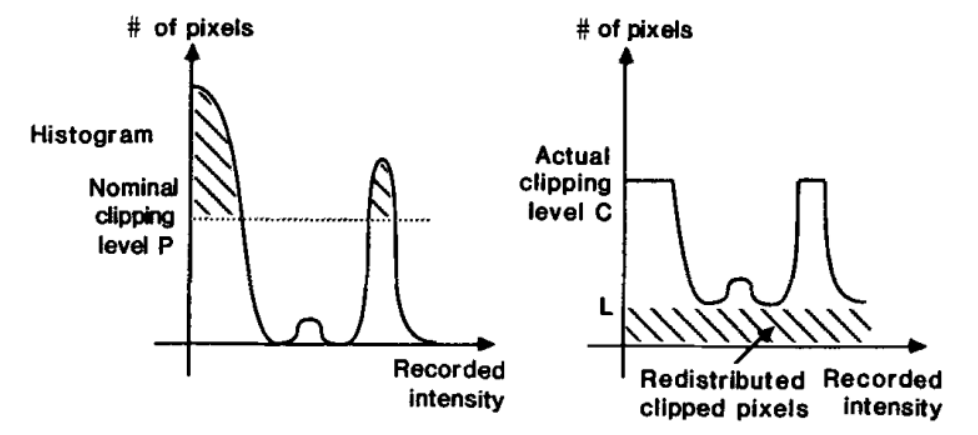
按照这个思路设计的算法就是 Contrast Limited Adaptive Histogram Equalization。
回头再来分析那个黑图像被对齐到全白的例子。如果用 CLAHE 来处理这个黑图,我们可以拍脑袋规定直方图每个 bin 的频数不能超过总像素数的 50%,超过的部分要被均摊到各个 bin 中。根据这个规定,像素 x=8 被映射成
y=P(8)=0.5*255=128.
CLAHE 把 x=8 的频数强制分给了其它 X 值,但是由于原图中并不存在所谓的其它 X 值,所以这部分频数实际上就浪费了,目标图中除了 128 之外,根本不会出现别的像素值。
以下图为例,由于 CLAHE 人为削减了最亮像素的频数,所以 CLAHE
图的亮区得到了抑制,而暗区的亮度得到了明显的提升。 
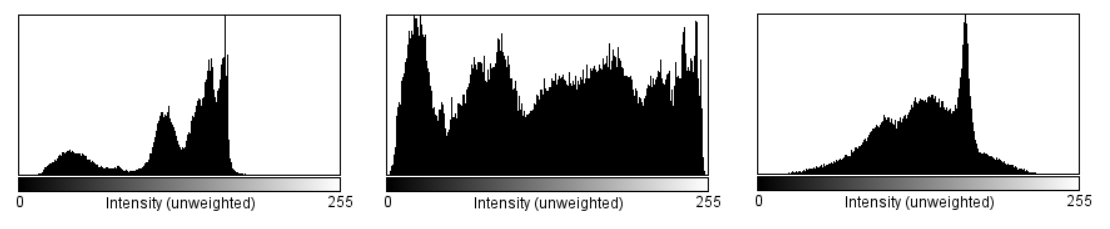
如果仔细分析图像质量的话,这个图的绿植效果其实并不好,绿得很不自然,可能还不如原图的效果。其实原图的主要问题是亮部对比度不足,需要拉伸,而暗部的直方图分布是没有太大问题的,不调整也可以。
从这个例子我们发现,被强制裁掉的频数该如何分配仍然是一个可以讨论的话题。有的时候可能直接丢弃了会比较好,如果舍不得丢,也可以考虑优先分配给离本主比较近的像素。
当然,单纯地限制像素频数无助于解决颜色数量不够导致的分色问题。如果需要改善分色问题,则还要引入抖色(dither)之类的机制,让原本一个颜色随机地抖动变成一些相近的颜色,以填补直方图中的空洞。从视觉效果上看,抖色相对于在图像中主动添加噪声,而噪声会模糊两层颜色之间的边界,起到平滑过渡的作用。
参考文献
https://zhuanlan.zhihu.com/p/150381937