Lens 之景深
景深的计算
相机景深:其指的是在某个物距之间,还能够清晰成像的距离: 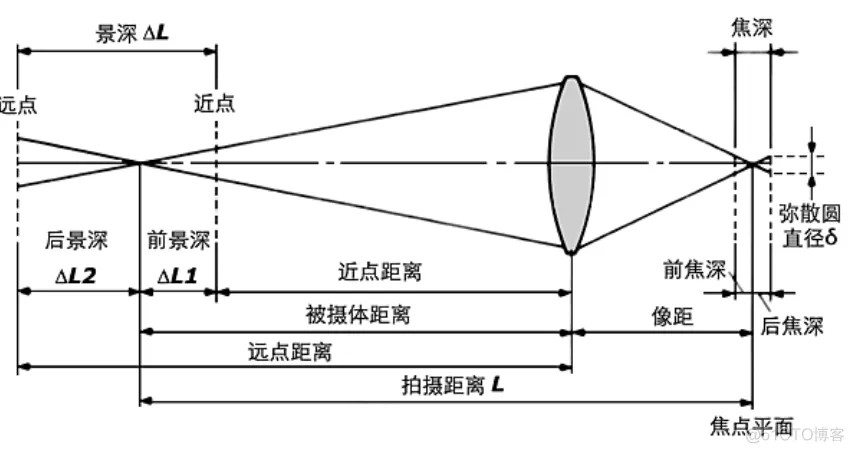
如果 sensor 刚好在像距的位置上,物体的一个点,成的像也就是一个点。如果 sensor 在像距的前面或者后面,这个点也就成了一个圆,专业术语叫弥散圆。当这个圆大到一定的程度的时候,照片也就糊了。
景深公式依据下列 6 个关系式:
其中 d 为光圈直径,f 为焦距,N 代表镜头设定的光圈值(2.8、4、5.6、8、11、22)等。
光学透镜成像公式(这个在光学原理一节有介绍,要通过相似三角形推导):
其中 v 代表像距、s 代表物距。
后物体的成像公式:
前物体的成像:
解以上方程组得:
景深三要素
光圈
光圈值,是镜头的焦距/镜头通光直径得出的相对值(相对孔径的倒数),光圈值越小,光圈越大。相同光圈值,sensor
表面的照度相同。光圈越大,景深越小。 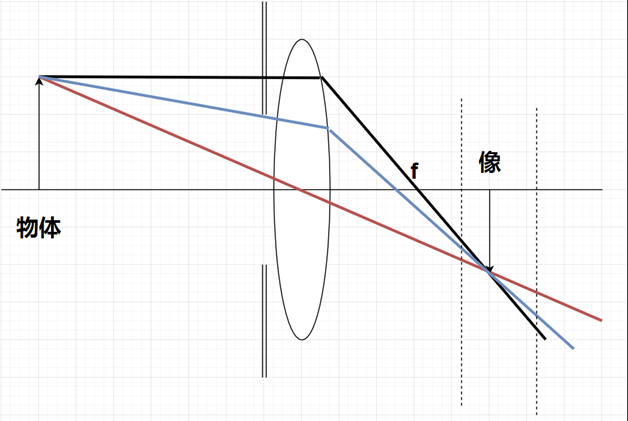
如图,当光圈减小,虚线位置的弥散圈也在减小。弥散圈越小,成的像就越清晰。原来看不清楚的物体,弥散圈变小了,就能看清了,景深就变大了。夜间摄影的时候,增大光圈可以提高进光量,提升图像质量,但是大光圈也会导致景深太小,这个时候就需要两者权衡。拍人像的时候,我们又会要求景深小,这样就有背景虚化的效果,这个时候就需要大光圈。
物距
物体越近,景深越小 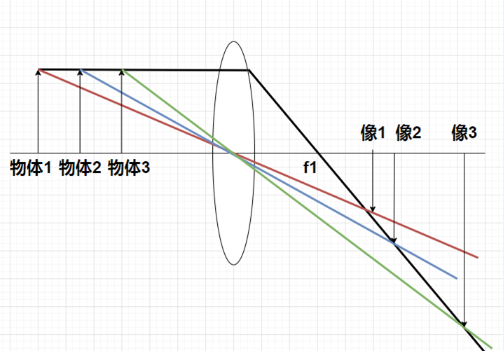
物体 123 是等距的,他们成的像分别是像 123,但是像的位置不是等距的。由于 sensor 聚焦好之后只能在一个位置上,在这个位置上能看到更多的物体,就是景深大。物体 1 比较远,我们将 sensor 聚焦在像 1 上,像 2 距离像 1 很近,弥散圈很小,很容易看清楚物体 2。相反的,物体 3 比较近,我们将 sensor 聚焦在像 3 上,像 2 离像 3 比较远,弥散圈大,不容易看清楚物体 2。所以从图中可以很容易的看出,物体越近,景深越小。
焦距
焦距越长,景深越小。 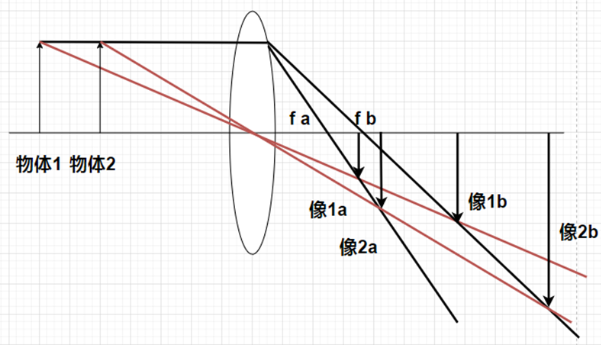
两个物体 1 和 2,焦距 fa < fb。当焦距为 fa,成的像分别是 1a 和 2a,当焦距为 fb 时,成的像分别为 1b 和 2b。当焦距比较小,为 fa 的时候,可以很明显的看到像 1a 和像 1b 距离很近,由于 sensor 只能固定在一个位置,更容易同时看清两个物体。因此焦距越短,景深越大。
| 景深 | 光圈 | 物距 | 焦距 |
|---|---|---|---|
| 大 | 小 | 近 | 短 |
| 小 | 大 | 远 | 长 |
景深与 Sensor 的关系
我们会有一个直观的理解就是弥散圆小于 cmos 的像原大小那么就不会对成像产生影响,就感觉景深变大了,实际上景深需要转换到等效参数下。 在等效焦距、等效光圈、对焦距离三者相同的条件下,不同尺寸的感光元件景深保持一致。其中焦距和等效焦距、光圈和等效光圈的换算普遍以 135 传感器为标准。
预览: