Sensor 的特性与噪声

CMOS sensor 的响应特性

理想 CMOS sensor 的响应特性下图所示：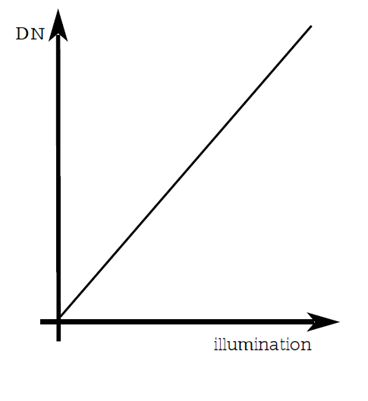

横坐标是光强，纵坐标是 cmos 输出信号，直线的斜率决定了单位输入能够激励的响应大小，这个斜率称为增益系数（gain）。sensor 会提供一组接口用于调节实际生效的增益值。

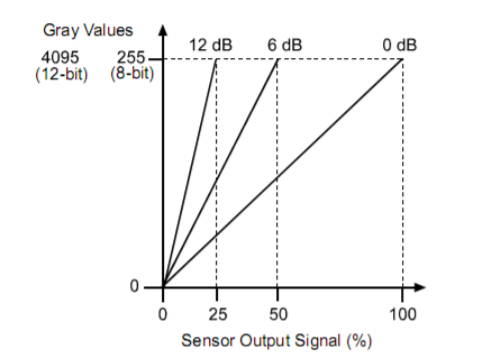
而实际的 sensor 只能是在一段有限的区间内保持线性响应，对于幅度过小或者过大的输入信号会不能如实地表示。

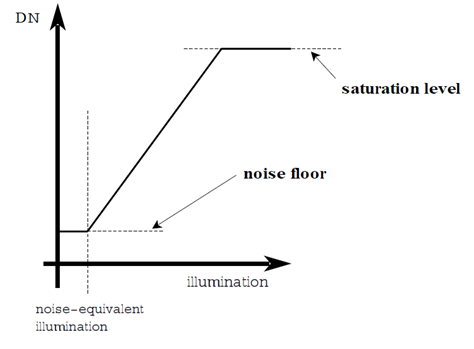
下图是实验测量的输入输出曲线，横坐标是入射到 sensor 的光子数，纵坐标是 sensor 输出的数值（Digital Number, DN）。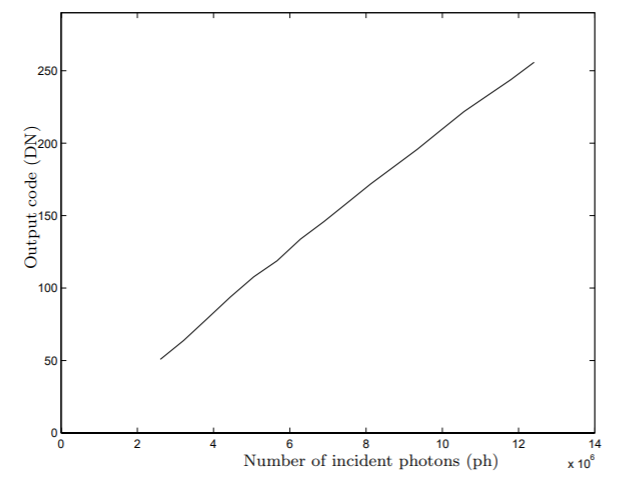

以上关系用公式描述就是：

\[ S(N,t) = q(\lambda) \cdot N \cdot t \]

其中，\(S(N, t)\) 是 sensor 的一个像素采集到的电子数， \(q(λ)\) 是 sensor 在波长λ处的光电转换效率，N 是单位时间内入射到 sensor 表面的光子数（波长λ的单色光），t 是曝光时间。

sensor 最终输出的像素值是使用 ADC 对 S(N,t) 进行采样和 AD 转换得到的量化值，该值会有 PV(Pixel Value)，ADU(Analog-Digital Unit)，DN(Digital Number)，Output Code 等多种表述方式，并且

\[ DN = g * S(N,t) \]

其中符号 g 代表增益系数 gain，意义是多少个光子能够激励出 1 个比特的 DN 值。

势阱容量 （Saturation Capacity）

势阱容量又称 Full Well Capacity，指一个像素的势阱最多能够容纳多少个光生电子，消费类的 sensor 一般以 2000~4000 较为常见，此值越大则 sensor 的动态性能越好。

下图是一些单反相机 sensor 的饱和阱容比较。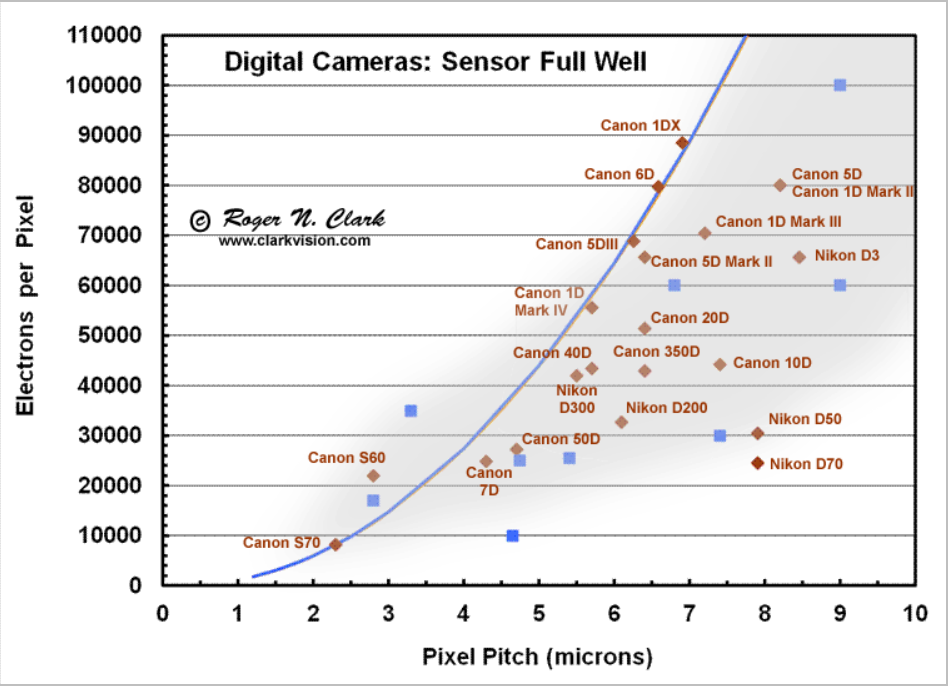

噪声 （Noise）

由于电子的无规则热运动产生的噪声在所有电子设备中普遍存在，器件的温度越高，电子的热运动越剧烈，产生的噪声也就越大。

假设照明强度恒定、均匀，相机拍摄图像中的噪声是测量信号中空间和时间振动的总和。下图以传递函数的形式总结了 CMOS sensor 光、电转换模型以及几种主要噪声的数学模型。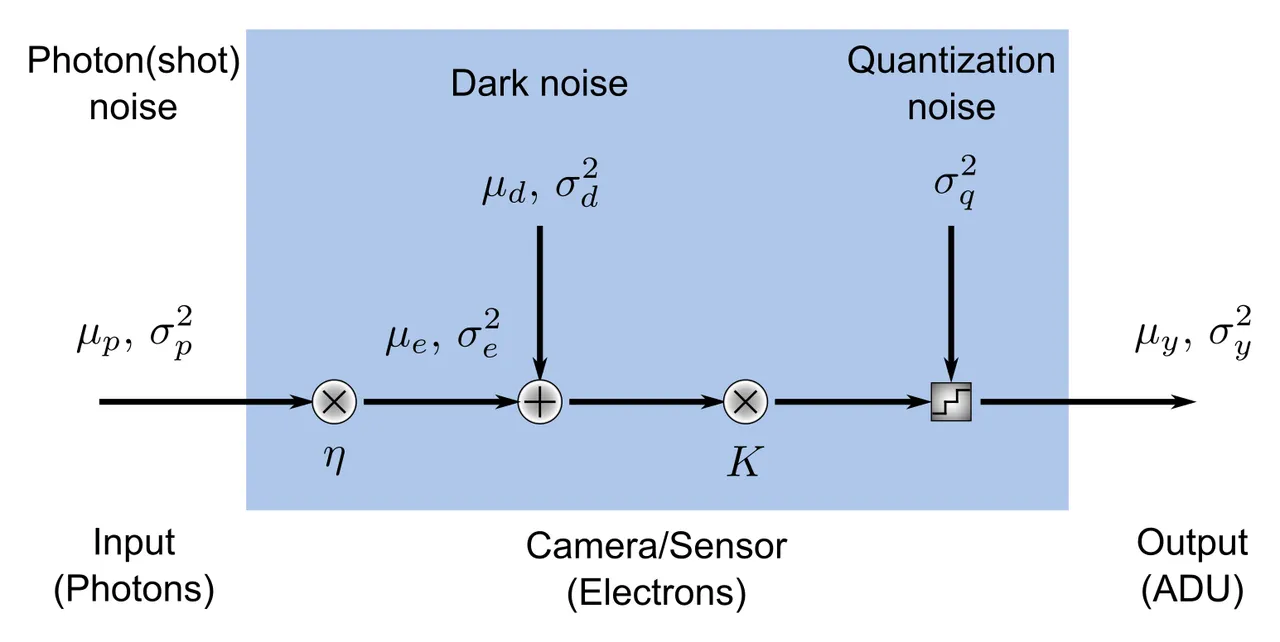

下图更加细致地描述了 CMOS sensor 成像过程中各种噪声的来源和作用位置。

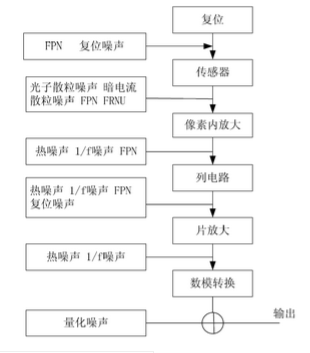
sensor 噪声中含有几部分分量：

• 暗散粒噪声 (σD): 硅片中电子的热运动会导致一些价电子随机激发至导带中形成暗电流（dark current），所以即使完全没有光子入射，sensor 也会存在一定的信号输出。暗散粒噪声在统计上服从泊松分布，与光信号的高低水平无关，但与传感器的温度有关，一般的规律是温度每升高 8°C 暗电流翻一倍。

• 读出噪声 (σR): 该噪声是在产生电子信号时生成的。Sensor 中使用 AD 转换器（ADC）将模拟放大器输出的模拟电压采样为数字电压。由于数字信号的精度总是有限的，通常为 10 比特至 14 比特，幅值位于两个相邻数字之间的模拟信号会四舍五入到最接近的数值，所以这个过程会引入量化噪声，这是读出噪声的重要组成部分。该噪声由传感器的设计决定，意义是至少需要多少个电子才能驱动读出电路的 ADC 变化一个比特。它与信号高低水平和传感器温度无关。

• 光子散粒噪声 (σS): Shot noise, 该噪声是与落于传感器像素上光子相关的统计噪声。在微观尺度下，光子流到达传感器的行为在时间和空间上都是不均匀的，整体上其统计规律符合泊松分布。光子散粒噪声是与被测信号的高低水平有关的，与传感器温度无关。

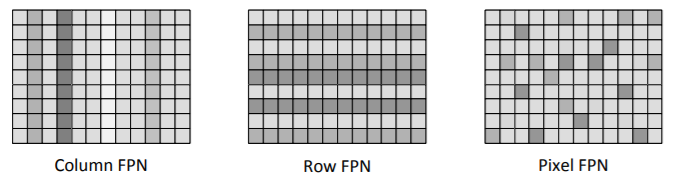
• 固定模式噪声 (σF): Fixed-pattern noise（FPN）, CMOS sensor 每个像素内都配置一个电荷电压放大器，每行、每列都有一些晶体管用于控制像素的复位和读出，这些器件的工作参数相对理论值的漂移就构成一种固定模式噪声。另外，坏像素、瑕疵像素也可以视为一种固定模式噪声。

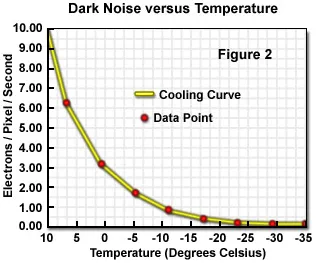
• 复位噪声 (σr): 卷帘曝光方式需要 先对势阱复位，将势阱中自由积累的电荷全部释放，为后续的读出准备。但是由于暗电流的存在，每次复位后都会残留一些大小随机的噪声信号，即复位噪声，其大小与像素结构、芯片温度、PN 结电容有关，因此也称为 kTC 噪声。像素的复位是需要一定时间的。定量的研究表明，即使是采用较大的复位电流，一般也需要 1ms 以上的时间才能将电荷释放干净，如下图所示。

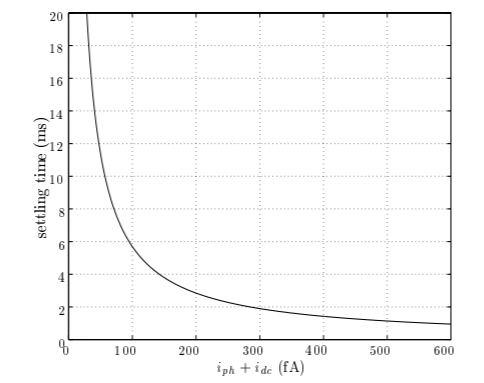
  实际的复位控制信号通常会短于 1ms，因此下一帧图像多多少少会残存一些上一帧图像的影子，这个残影叫做 image lag，也是噪声的一种形式。

• 1/f 噪声 (σf): 1/f 噪声是一种低频噪声，在有些文献中也称 flicker noise（闪烁噪声） 或 pink noise（粉红噪声），它广泛存在于半导体器件中。在低频的时候 1/f 噪声一般显著高于电散粒噪声。一种理论认为，半导体晶格中都会存在一些缺陷，这些缺陷能够捕获一些自由电子并将其束缚一段时间，这可以解释 1/f 噪声的一种来源。

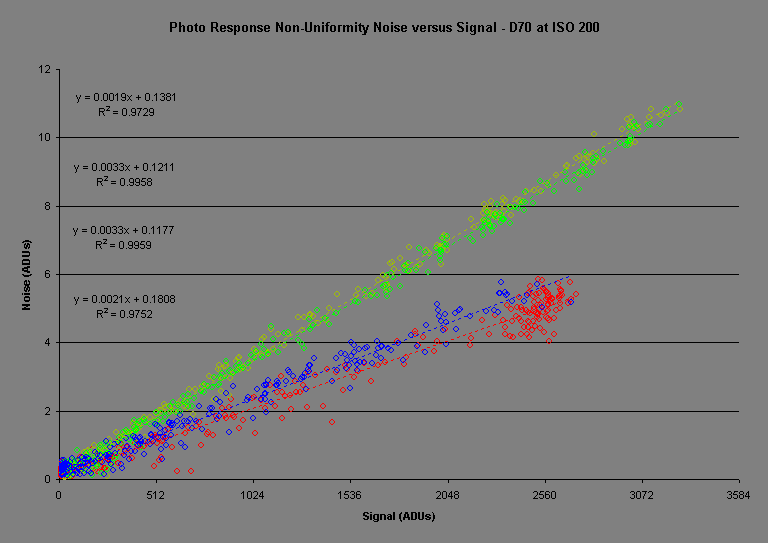
• 光响应非均匀性 (σp): 英文为 PRNU，Photo Response Non-Uniformity。Bayer 格式的 sensor 通常存在四种像素 (R,Gr,Gb,B)，这四种像素的光电转换特性（即增益特性）不可能是完全一样的，不同种像素间存在种间差异，同种像素之间也存在个体差异，如下图所示：

• 串扰： 英文为 Crosstalk，在通信领域中指两条信号线之间由于屏蔽不良而发生了的信号耦合，在 sensor 领域，串扰指的是入射到一个像素 A 的光信号没有在这个像素里被捕获，反而被其周围的像素 B 捕获，导致 B 产生了不该有的信号。

在下图例子中，粉色表示的是不透光的像素，不应该有任何输出，黄色表示正常像素，应该有输出。实际上，光子是可以在硅片中穿透一定的距离的，从而有机会进入到粉色像素的感光区，从而变成粉色像素的信号，这就是 CMOS sensor 的串扰机制。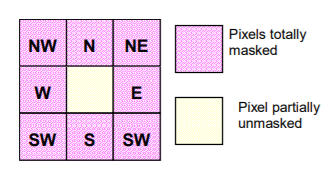

从下图可以看出，波长越长，串扰越严重，某些像素位置串扰能量可以达到 5%。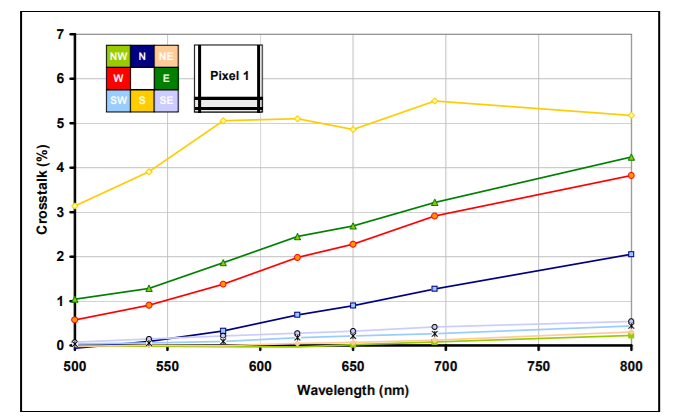

甚至可以进一步将量化噪声吸收到读出噪声中，于是每个像素的总有效噪声是下列所有噪声的总和：

\[ \sigma_{eff} = \sqrt{\sigma_D^2 + \sigma_R^2 + \sigma_S^2} \]

噪声模型

PRNU 体现的是红、绿、蓝三种像素的增益差异，对于任一种像素，光信号越强像素值抖动越大，这体现了光信号本身的散粒噪声，光信号为零时，输出幅度最小的像素体现了半导体的暗散粒噪声，而 红、绿、蓝三种像素之间的差异体现了 FPN 噪声。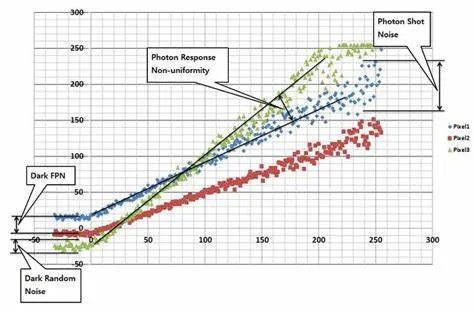

尽管像素噪声有多种来源，但每种噪声的贡献程度并不是同等重要的。为了简化计算，实际上经常采用简化的噪声模型，只考虑光散粒噪声、暗散粒噪声、读出噪声、以及 ADC 器件的量化噪声，如下图所示。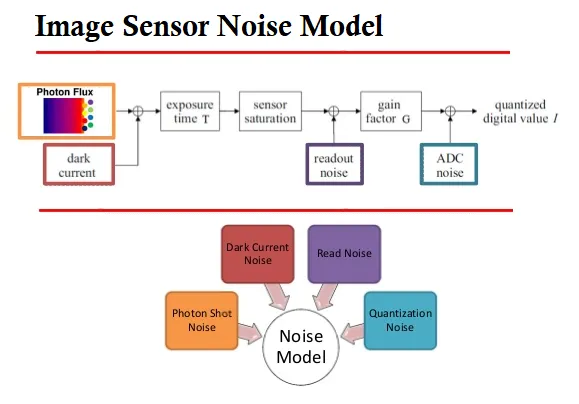

信噪比 （SNR）

信噪比是一个电子设备或者电子系统中信号与噪声的比例，如下图所示。这里面的信号指的是来自设备外部需要通过这台设备进行处理的电子信号，而噪声是指该设备自行产生的无规则信号，并且该种信号并不随外部输入信号的变化而变化。

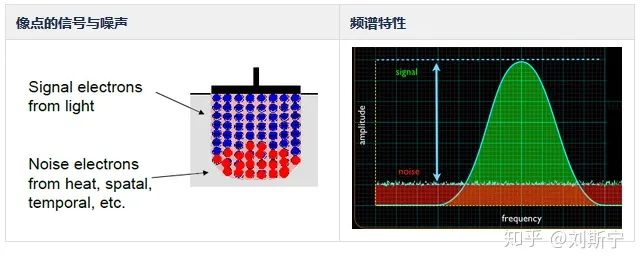
下面分析 sensor 图像的信噪比。如前所述，设 S 为传感器上每个像素上入射光子通量为 N 光子/秒情况下产生的“信号”电子的数量，其中量子效率为 QE，曝光时间为 t 秒，那么：

\[ S = (Q E)Nt \]

通过 S，可以将光子散粒噪声表示为：

\[ \sigma_s = \sqrt{(Q E)Nt} \]

信噪比（SNR）可以由下式进行估算：

\[ SNR = \frac{S}{\sigma_{eff}} \]

前面已经提到：

\[ \sigma_{eff} = \sqrt{\sigma_D^2 + \sigma_R^2 + \sigma_S^2} \]

下图给出了 sensor 信号（光电子数 S）与噪声 (σeff) 之间的关系和变化规律。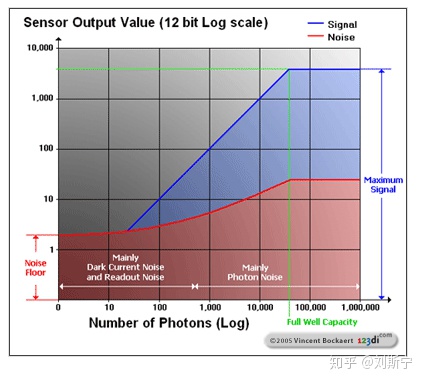

传感器在光子数达到一个阈值后才开始有信号的（图上是在 10 与 100 个光子之间），如果传感器接受的光子数少于某个阈值，就不会有信号输出。这个阈值一般认为是读出噪声。在像素达到饱和前，光电子数随着入射光子数的增加而线性增加，而噪声随入射光子数增加按根号规律增加，噪声增加的速率低于信号增加的速率，因此总的信噪比不断增长。

当 S 很小时，SNR 主要由σR 决定，即 sensor 暗电流和读出噪声是主要来源。当 S 很大时，SNR 主要由σS 决定，即光信号本身的统计涨落是噪声的主要来源。

一般认为，SNR=10dB 是可接受（acceptable）的图像质量标准，该值意味着信号幅度是噪声的 3.16 倍。而 SNR=40dB 是优秀（excellent）的图像质量标准，该值意味着信号幅度是噪声的 100 倍，因此至少需要 10000e-饱和阱容。介于中间的是 SNR=30dB，该值要求像素提供 1000e-以上的饱和阱容，这刚好是很多手机 sensor 的指标范围。

下图是一些单反相机的典型 SNR 对比。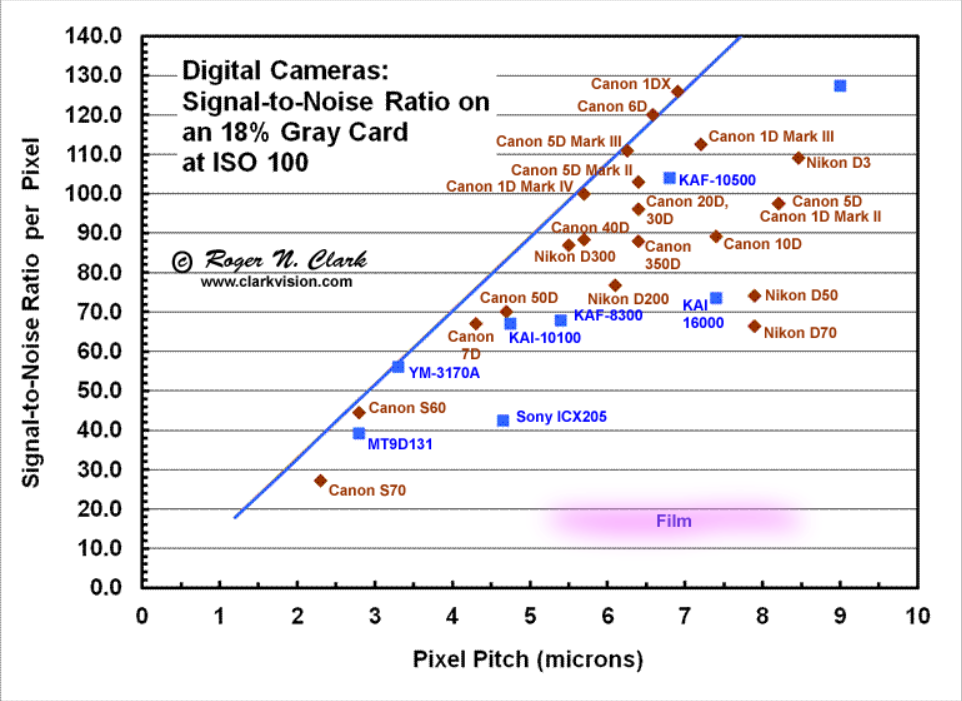

下图是 Canon 1D3 单反相机在不同 ISO 下的信噪比曲线，横坐标是曝光量，纵坐标是 SNR，都是以"stop"为单位，即以 2 为底的 log-log 坐标。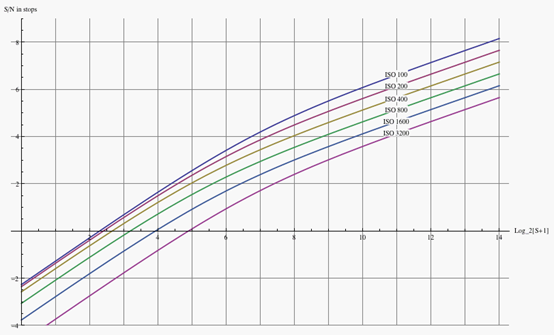

动态范围 （Dynamic Range）

一个信号系统的动态范围被定义成最大不失真电平和噪声电平的比值，在实际应用中经常用以 10 为底的对数来表示，单位是分贝。对于胶片和感光元件来说，动态范围表示图像中所包含的从“最暗”至“最亮”的取值范围。根据 ISO15739 的定义，“最亮”指的是能够使输出编码值达到特定“饱和值”的亮度；而“最暗”指的是图像信噪比下降至 1.0 时的亮度。

sensor 动态范围越大，所能表现的层次越丰富，所包含的色彩空间也越广。下图是用来测量 sensor 动态范围性能的常用方法。

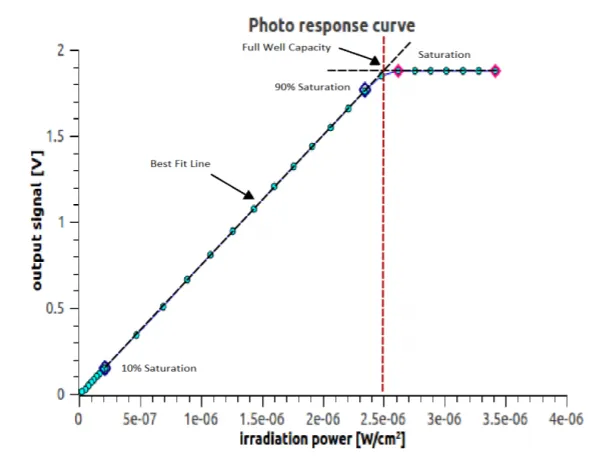
前面已经提到，sensor 是由数以百万个甚至更多像素组成的，这些像素在曝光过程中吸收光子转化成电荷。一旦这些像素容量达到饱和，多余的电荷便会溢出导致输出信号不再增加，此时像素的值不能反映光信号的真实强度，如下图所示。

根据动态范围的定义，sensor 动态范围的分贝表示用以下公式计算：

\[ DR = 20log(\frac{FullWellCapacity}{ReadOutNoise}) \]

根据上面的公式可以简单计算出动态范围与 FullWellCapacity 之间的关系。

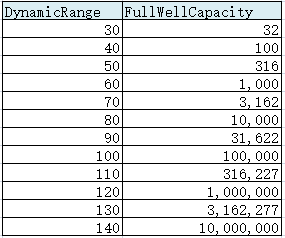
显然，目前较好的工艺水平（SONY）可以做到每个像素容纳 10000 ~ 30000 个电子，可以提供 80 ~ 90dB 的极限动态范围，但是更多就不合理也不经济了，因为更大的势阱容量需要更大的像素面积，而像素大到一定程度之后就会遇到成品率瓶颈。

下图列举了一些典型单反相机 sensor 的动态范围指标，纵坐标可以理解为 AD 转换器的位数。例如 12 位 ADC 能够表示的动态范围是 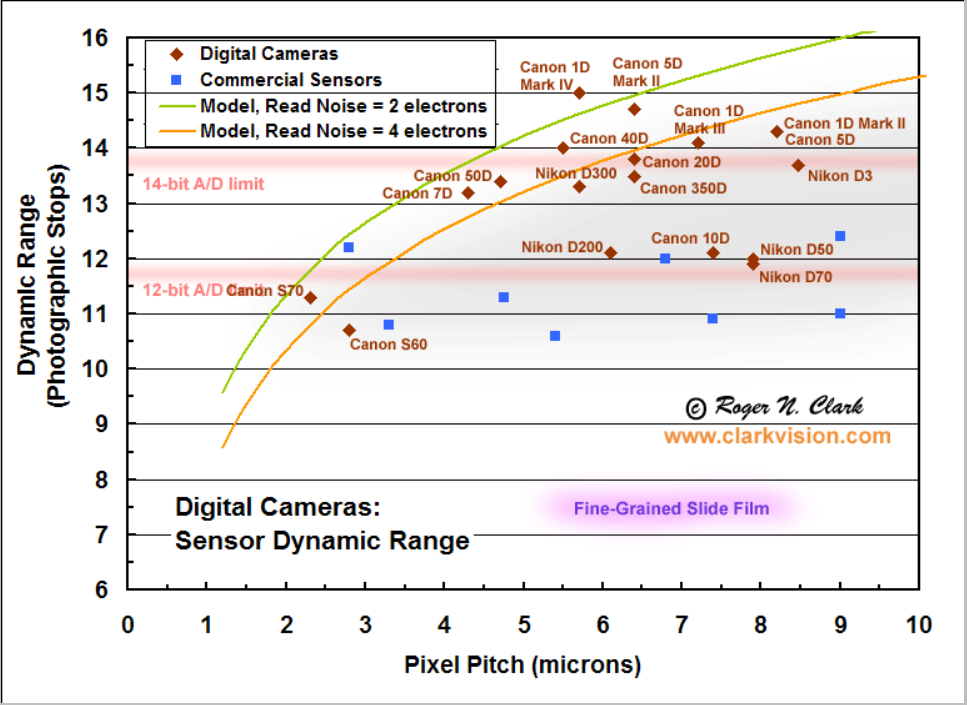\(2^{12} = 4096\)，而 14 位 ADC 能够表示 \(2^{14}=16384\) ，以此类推。

PS: ADC 位数的选择必须是和 sensor 的动态范围相适配的，ADC 位数高于 sensor 是没有任何意义的性能浪费，低于 sensor 则不能完全发挥出 sensor 的性能优势，也是一种性能浪费。从图中可以看到，单反相机的主流是采用 14 位 ADC，更高端的则采用 16 位 ADC。

灵敏度 （Sensitivity）

CMOS sensor 对入射光功率的响应能力用灵敏度参数衡量，常用的定义是在 1μm2 单位像素面积上，标准曝光条件下 (1Lux 照度，F5.6 光圈），在 1s 时间内积累的光子数能激励出多少 mV 的输出电压。

在量子效率一定的情况下，sensor 的灵敏度主要取决于电荷/电压转换系数 (Charge/Voltage Factor, CVF)。在下图的例子中，CVF =220uV/e，这意味着阱容 2000e 的像素能够激励出最大 440mV 的电压信号。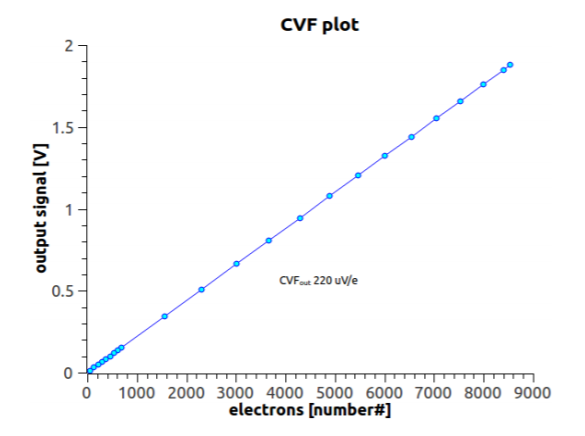

在曝光、增益相同的条件下，灵敏度高的 sensor 信噪比更高，这意味着至少在两个方面可以获得比较优势，

• 在图像噪声水平接近的情况下，灵敏度高的 sensor 图像亮度更高、细节更丰富。
• 在图像整体亮度接近的情况下，灵敏度高的 sensor 噪声水平更低，图像画质更细腻。

EMVA 1288 定义了评价 camera 灵敏度的标准，即多少个光子可以引起 camera 像素值变化 1，即一个 DN。根据量子力学的公式：

\[ E_p = \frac{h \cdot c}{\lambda } \]

1 个波长为 540 nm 的绿光光子携带的能量是：

\[ E_p = 3.683 \times 10^{-19}[J] \]

Camera 技术手册中会给出像素灵敏度规格：

根据此规格即可计算像素值变化 1 需要多少个光子。

参考文献

https://zhuanlan.zhihu.com/p/100777121