基于陀螺仪的视频稳定非线性滤波器
Abstract
我们提出了一种对移动设备上捕获的视频进行视频稳定和滚动快门校正的方法。该方法使用来自机载陀螺仪的数据来跟踪相机的角速度,并且可以在相机捕获期间内实时运行。我们消除了由于手抖动引起的小抖动和滚动快门失真,营造出在三脚架上拍摄的视频的效果。
我们提出了一种对移动设备上捕获的视频进行视频稳定和滚动快门校正的方法。该方法使用来自机载陀螺仪的数据来跟踪相机的角速度,并且可以在相机捕获期间内实时运行。我们消除了由于手抖动引起的小抖动和滚动快门失真,营造出在三脚架上拍摄的视频的效果。
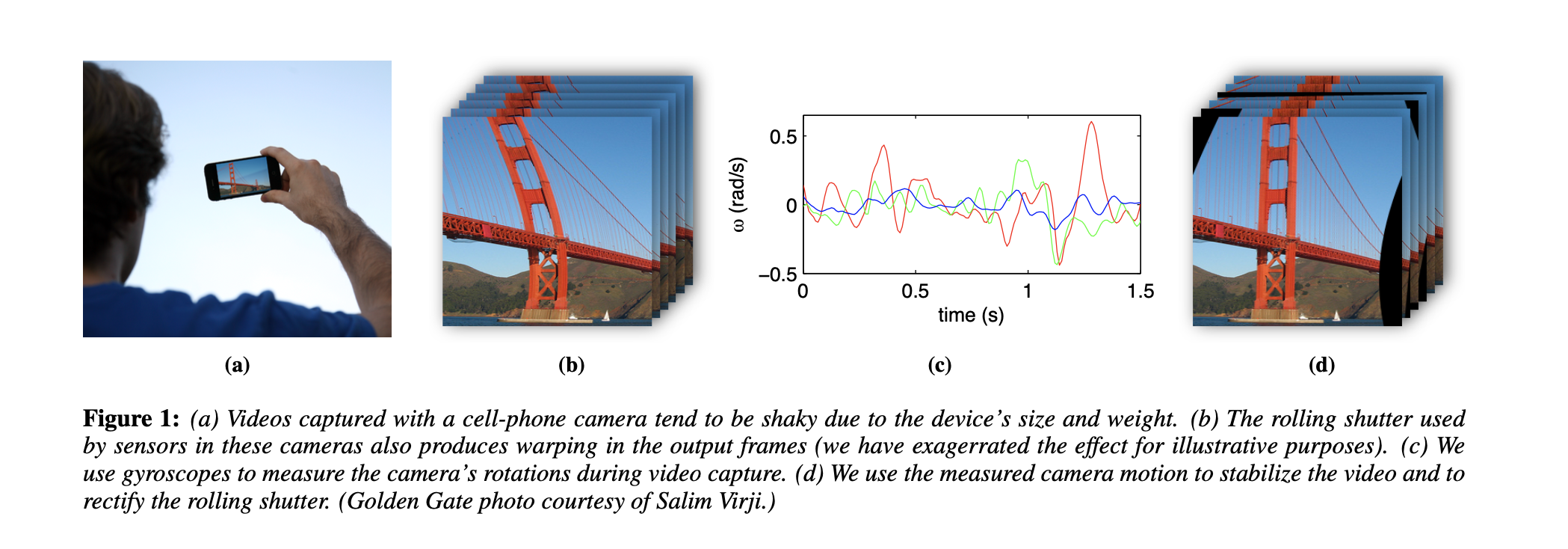
在本文中,我们提出了一种基于商用陀螺仪的强大实时视频稳定和滚动快门校正技术。首先来对相机运动和卷帘快门扭曲进行建模,然后从单个视频捕获自动校准陀螺仪和相机输出。 这种校准使我们能够仅使用陀螺仪数据来有效校正卷帘快门扭曲并稳定视频。
在本文中,我们提出了一种混合方法来估计运动并通过切换函数稳定视频,该方法在 Kanade-Lucus-Tomasi (KLT) 跟踪器和 IMU 辅助运动估计器之间切换估计的运动。为了实现这一点,由于 KLT 跟踪器在较大运动期间的性能不佳,我们使用 KLT 跟踪器来校正低旋转的运动,并使用 IMU 辅助运动估计器来校正高旋转,此外,卡尔曼滤波器用于去除不需要的运动,从而平滑轨迹。
这里以小孔成像模型为例,全相模型是相同的流程只是投影模型不一样而已。在相机校准模型一文中已经介绍了将像素坐标系变换到相机坐标系中 相机校准模型 如下:
\[ \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{d_x}& 0 &u_o \\ 0 & \frac{1}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \frac{1}{z_c}\begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_c\\ y_c\\ z_c \end{bmatrix} \]
这里我们取 \(z_c = 1\) 再做一个变换得到:
\[ \begin{bmatrix} x_c\\ y_c\\ z_c \end{bmatrix} =\begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} ^{-1} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} \]
我们记 :
\[ K_{内参}^{-1} = \begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} ^{-1} \]
则将像素坐标系与该矩阵相乘就可以将像素坐标系转换到相机坐标系上,待后面使用。
具体可以参考 imu 姿态解算 一文,我们需要对 IMU 数据做三件事情:
IMU 坐标系对齐相机坐标系,这一步目的为了将 IMU 的正交三轴数据与 Camera 坐标系对齐。
卡尔曼滤波:为了消除 IMU
的系统误差以及如果要做重力矫正需要做姿态解算(重力对齐)。这里常用的就是卡尔曼滤波和
mahony
滤波,这一层滤波的目的就是为了得到更为准确的相机姿态和相机抖动状态,如下图所示:
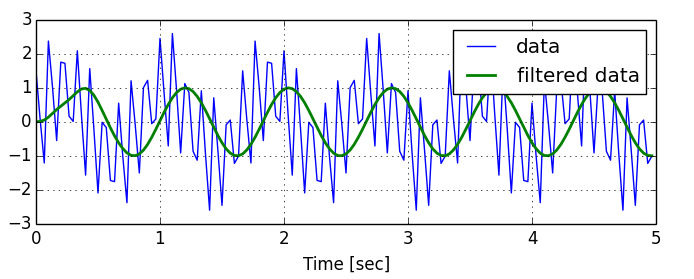
平滑滤波:在我们得到相机的抖动状态就可以对相机的姿态做一个平滑滤波(可以采用四元数求平均,或者高斯滤波等算法),这个平滑滤波的目的是为了得到相机防抖后想要得到的状态。
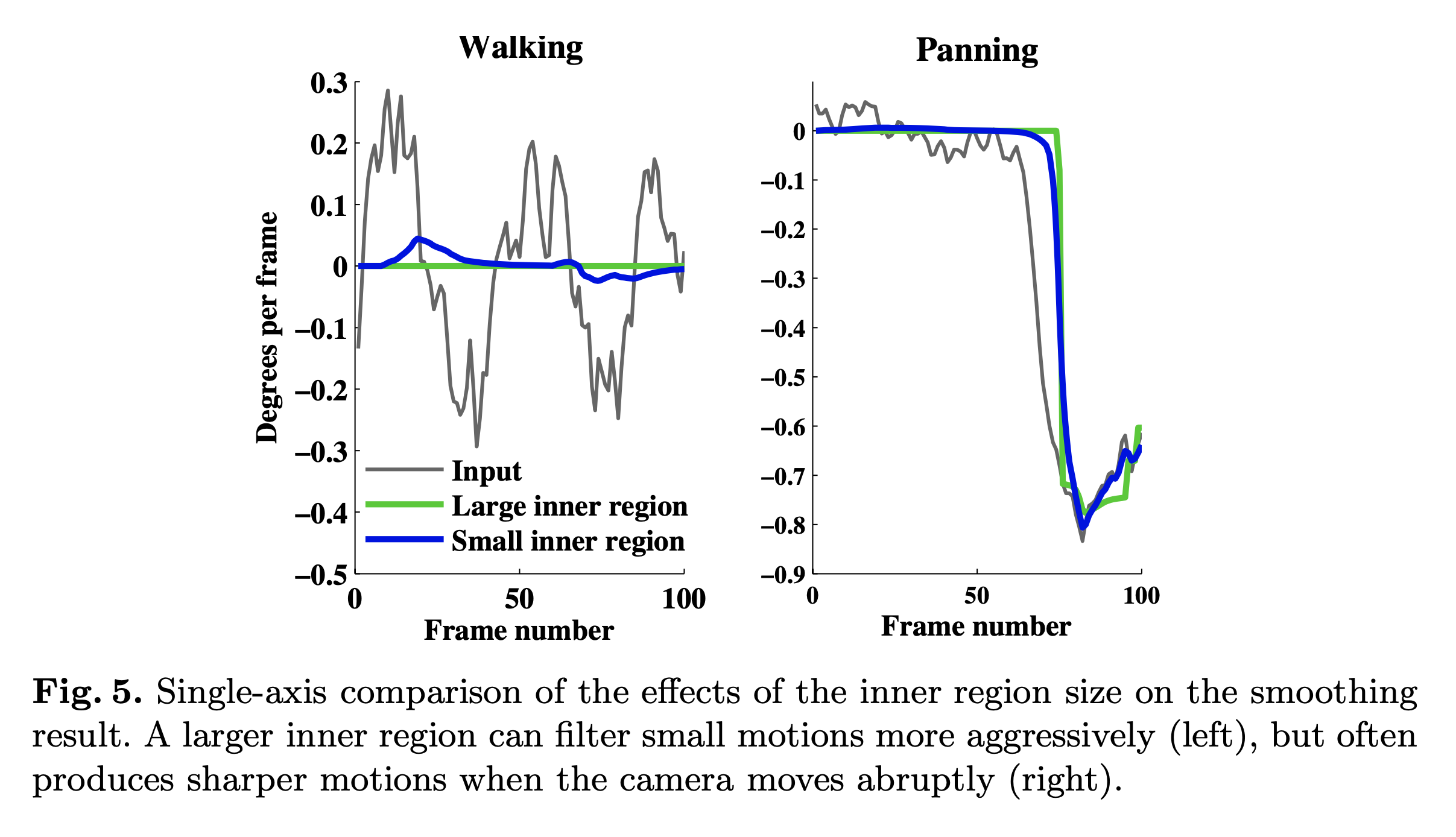
我们将从 Large inner region 曲线或者 Small inner region 曲线到 Input 曲线的变换矩阵记为 \(M(\alpha, \beta, \gamma)\) 为了简化模型这里面的数据是已经将 IMU 坐标系变化到相机坐标系下的变换矩阵。
到这里我们就得到了两条曲线和一个变换矩阵。
这里我们记旋转矩阵为:
\[ \begin{aligned} M(\alpha, \beta, \gamma) & =\left[\begin{array}{ccc} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{array}\right] \\ & =\left[\begin{array}{ccc} \cos \gamma \cos \beta & -\sin \gamma & \cos \gamma \sin \beta \\ \sin \gamma \cos \beta & \cos \gamma & \sin \gamma \sin \beta \\ -\sin \beta & 0 & \cos \beta \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{array}\right] \\ & =\left[\begin{array}{ccc} \cos \gamma \cos \beta & -\sin \gamma \cos \alpha+\cos \gamma \sin \beta \sin \alpha & \sin \gamma \sin \alpha+\cos \gamma \sin \beta \cos \alpha \\ \sin \gamma \cos \beta & \cos \gamma \cos \alpha+\sin \gamma \sin \beta \sin \alpha & -\cos \gamma \sin \alpha+\sin \gamma \sin \beta \cos \alpha \\ -\sin \beta & \cos \beta \sin \alpha & \cos \beta \cos \alpha \end{array}\right] \end{aligned} \]
综合前面两节的内容我们可以通过如下公式得到投影变换矩阵 R:
\[ R = K_{内参}^{-1} \ast M(\alpha ,\beta ,\gamma ) \ast K_{内参} \]
改写成完整的公式如下:
\[ R = \begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix}^{-1} \ast \left[\begin{array}{ccc} \cos \gamma \cos \beta & -\sin \gamma \cos \alpha+\cos \gamma \sin \beta \sin \alpha & \sin \gamma \sin \alpha+\cos \gamma \sin \beta \cos \alpha \\ \sin \gamma \cos \beta & \cos \gamma \cos \alpha+\sin \gamma \sin \beta \sin \alpha & -\cos \gamma \sin \alpha+\sin \gamma \sin \beta \cos \alpha \\ -\sin \beta & \cos \beta \sin \alpha & \cos \beta \cos \alpha \end{array}\right] \ast \begin{bmatrix} \frac{f}{d_x}& 0 &u_o \\ 0 & \frac{f}{d_y}& v_0\\ 0 & 0 & 1 \end{bmatrix} \]
该公式是通过相机的内参矩阵将像素坐标系变换到相机坐标系,然后通过 IMU 得到相机的姿态,将相机坐标系变换到世界坐标系下对相机的姿态进行稳定,得到稳定后的相机姿态,再将上述矩阵的逆乘起来变换回像素坐标系。这样就得到了透视变换的矩阵,将像素的坐标与该 R 矩阵相乘就得到了该像素防抖后的坐标值(就是 opencv 里的 remap)。
V4L2 是专门为 linux 设备设计的一套视频框架,其主体框架在 linux 内核,可以理解为是整个 linux 系统上面的视频源捕获驱动框架。其广泛应用在嵌入式设备以及移动端、个人电脑设备上面,市面上的编码产品类如:SDV、手机、IPC、行车记录仪都会用到这个框架来进行视频采集。
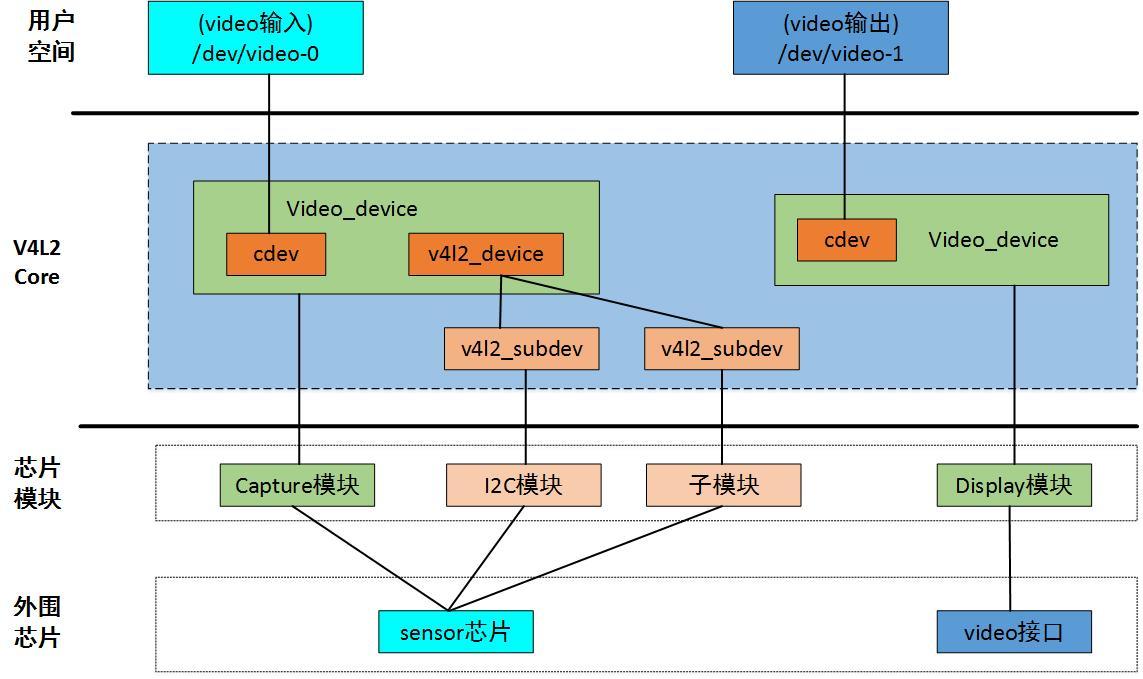
该图描述了 v4l2 驱动框架的整体结构,v4l2 本质上也是一个字符设备驱动程序,图中芯片模块对应 Soc 的各个子模块,video_device 结构体主要用来控制 Soc 的 video 模块,v4l2_device 会包含多个 v4l2_subdev ,每个 v4l2_subdev 用来控制各自的子模块,某些驱动不需要 v4l2_subdev ,依靠 video 模块就能实现功能。
该框架旨在提供标准内核接口来控制电压和电流 Regulator。其目的是允许系统动态控制 Regulator 功率输出,以节省功率并延长电池寿命。 这适用于电压 Regulator(电压输出可控)和电流 Regulator(电流限制可控)。
RTC 和系统时钟有不同的用途。前者是硬件时钟,以非易失方式维护绝对时间和日期,而后者是内核维护的软件时钟,用于实现 gettimeofday(2)和 time(2)系统调用,以及在文件上设置时间戳等。系统时钟报告从起点开始的秒和微秒,起点定义为 POSIX 纪元:1970-01-0100:00:00 +0000(UTC)。
CCF 主要用于系统 clock 的管理等操作。clk 的种类说明: 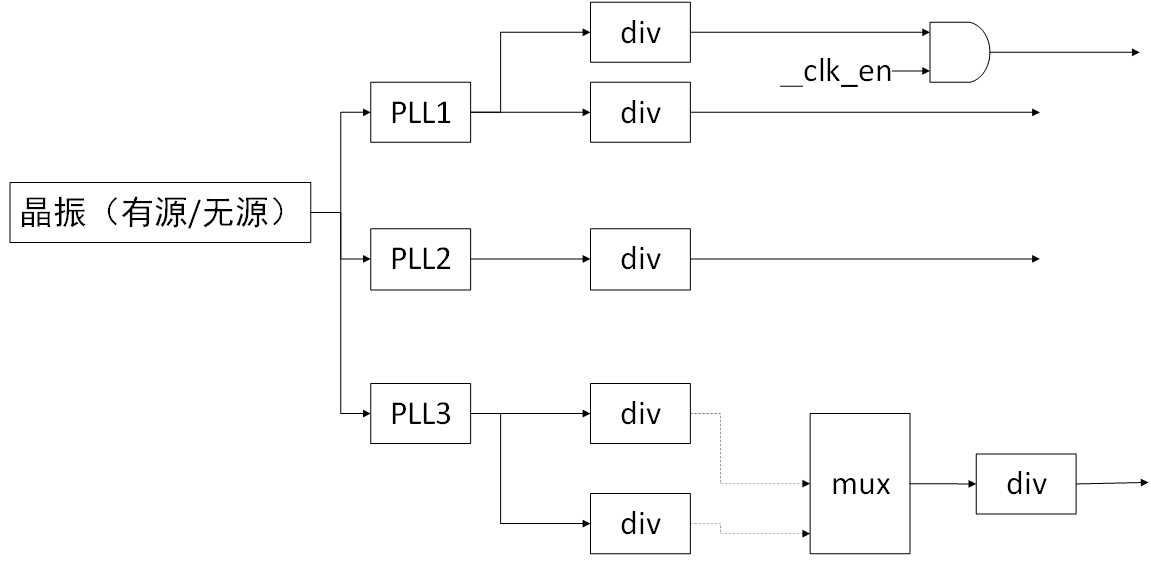
如上图所示,时钟源大概可分为如下几种:
而在 CCF 子系统的抽象中,这五种均抽象为 clk,但是针对这 5 种类型的时钟也提供了单独的时钟注册函数(也就是对 clk_register 函数的封装,并针对不同的时钟类型定义了不同的结构体)。
在 CCF 子系统中,针对硬件时钟的操作接口,也抽象了对应的结构体 struct clk_ops,包含时钟的使能接口、时钟频率的修改接口等等。而针对上述所说的不同种类的时钟源,其并不需要实现所有 struct clk_ops 中定义的接口。针对“时钟使能的与门电路”而言,仅需要实现 enabel、disable、is_enable 接口即可;针对多路时钟源选择的 mux 而言,则需要实现父时钟源的设置及获取的接口 set_parent、get_parent 等;对于倍频、分频而言,则需要实现时钟频率相关的接口 set_rate、recalc_rate 等。
按键输入、键盘、鼠标、触摸屏等等这些都属于输入设备,按键和键盘就是代表按键信息,鼠标和触摸屏代表坐标信息,因此在应用层的处理就不同。为此
input 子系统分为 input 驱动层、 input 核心层、 input
事件处理层,最终给用户空间提供可访问的设备节点,input 子系统框架如图
所示: