物理学基础概念

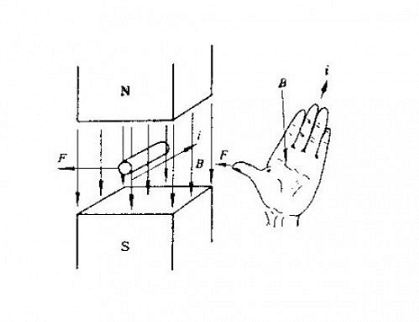
左手定则

将左手的食指，中指和拇指伸直，使其在空间内相互垂直。食指方向代表磁场的方向（从 N 级到 S 级），中指代表电流的方向（从正极到负极），那拇指所指的方向就是受力的方向。可用于判断安培力（运动导体所受到的力）和洛伦兹力（运动电荷所受的力）。

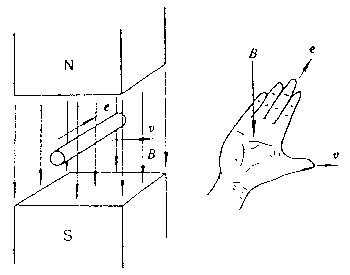
右手定则

伸开右手，使拇指与其余四个手指垂直，并且都与手掌在同一平面内；让磁感线垂直于手心进入，并使拇指指向导线运动方向，这时四指所指的方向就是感应电流的方向。用于判断导体在做切割磁场时产生的电流方向。

概述

openshoe 是一种通过惯性测量元件 (IMU) 来对运动进行积分以得到路径的控制算法。算法的核心是 ZUPT（零速度更新算法），在只有 IMU 惯性测量元件的情况下获得路径只能通过对加速度积分得到速度，再将速度对时间进行积分得到路径，这里如果不能对积分得到的速度进行有效的校正那么这个速度误差会时刻对时间进行积分，导致路径完全失效，因此必须采取有效手段及时对速度误差进行校正以得到较为准确的路径信息，ZUPT 就是一种基于检测零速度进行路径积分校正的算法。该算法的关键是对零速度的准确检测。

零速度检测算法

openshoe 采用广义似然检测算法对零速度进行检测，以判断 IMU 是否处于静止状态。

广义似然检测原理

要理解广义似然检测原理需要先熟悉几个概率论中相关的概念，详细如下：

传感器误差模型

对于理想的 IMU 三轴加速度计两两正交，构成一个正交的三轴直角坐标系，加速度计每一轴单独测量该轴的加速度，而陀螺仪则测量该轴的角速度。在实际的真实 IMU 中由于制造工艺的误差，三个坐标轴不可能完全两两正交，加速度计与陀螺仪的坐标系也不会完全重合，并且单个传感器也不是完全精确的。在实际器件中将数字输出量转化为实际物理量的 scale 参数在不同轴上是不同的，但是设备生产商都会提供一个默认的 scale 参数用于转换所有轴的数据，而且数字量的输出还会受到零偏（传感器在静止情况下也会有微小量的输出）的影响，这些就是造成 IMU 传感器的系统误差。

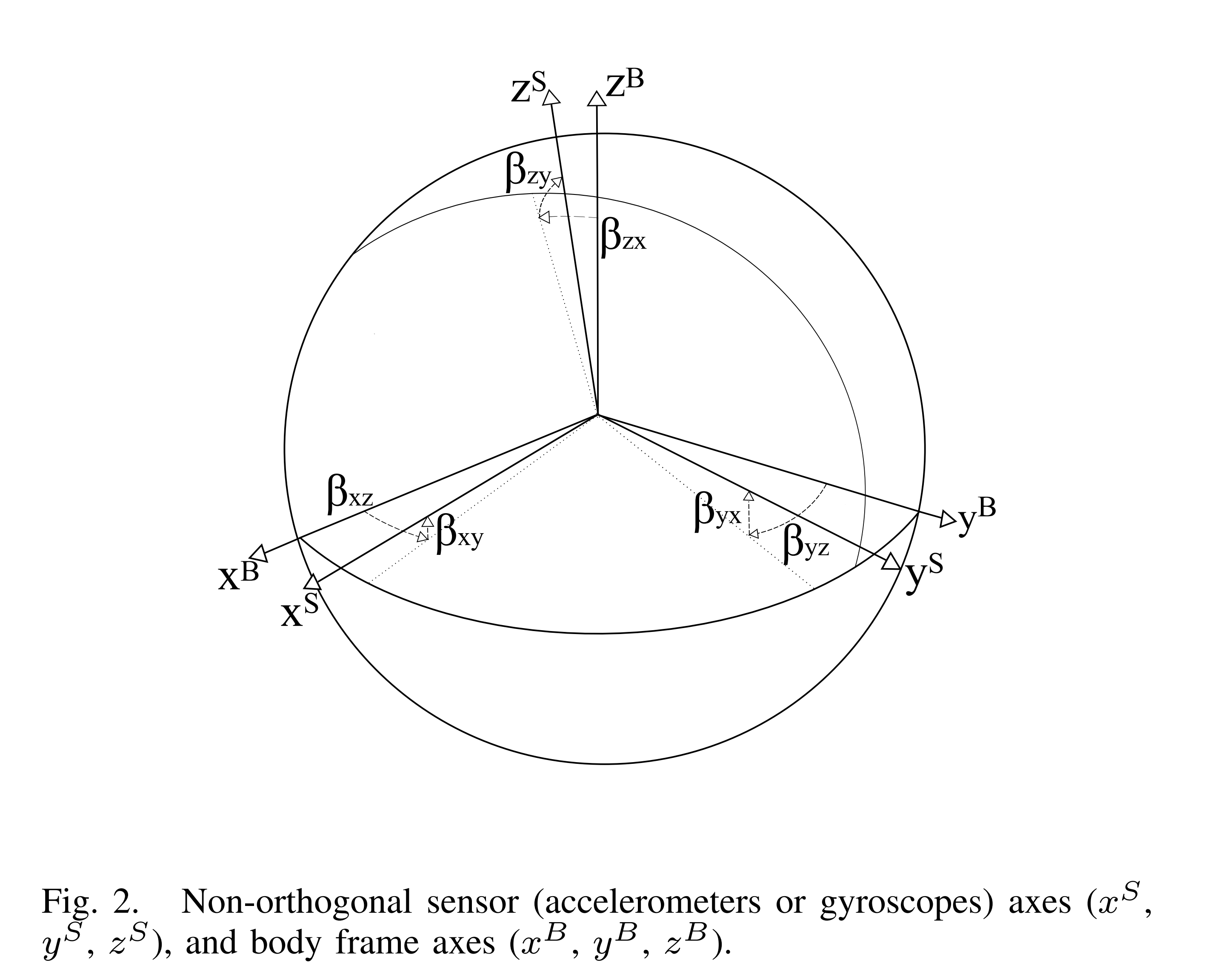
我们取实际器件的加速度计坐标系为 AF, 陀螺仪坐标系为 GF，根据 AF 和 GF 分别建立对应的正交坐标系 AOF 和 GOF，其建立约束为

• AOF 的 x 轴与 AF 的 x 轴重合。
• AOF 的 y 轴位于 AF 的 x 与 y 轴的平面中。

对于 GOF 的建立约束与 AOF 的约束类比建立。最后再建立一个正交机体坐标系 BF，BF 通常与 AF 和 GF 之间有一个小角度的偏差。在非正交坐标系（AF 或 GF）中测量得到的物理量\(s^S\)可以转换到机体坐标系 BF 中得到\(s^B\)于是得到下式：

\[ s^B = Ts^S, T = \begin{bmatrix} 1 & -\beta_{yz} & \beta_{zy} \\ \beta_{xz} & 1 & -\beta_{zx} \\ -\beta_{xy} & \beta_{yx} & 1 \end{bmatrix} \tag{1} \]

\(s^B 和 s^S\) 表示加速度或角速度在机体坐标系 BF 和加速度坐标系 AF 或陀螺仪坐标系 GF 下测量表示量，\(\beta_{ij}\) 表示加速度或陀螺仪的 i 轴绕机体坐标系 BF 的 j 轴的旋转角度。如图二所示：

IMU 通过加速度计解算姿态角

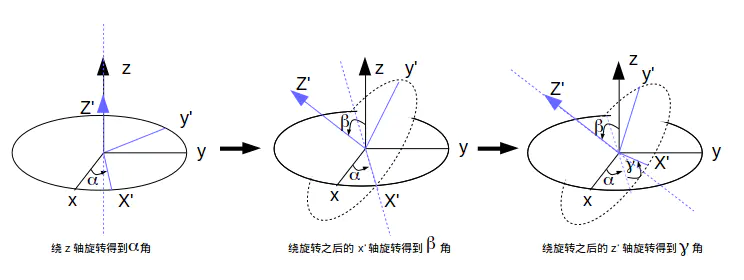
通过三角函数可以将加速度计三个轴的角速度解算为姿态角，其中 \(\alpha\) , \(\beta\) 和 \(\gamma\)（ \(\gamma\) 是 z 轴与重力加速度之间的夹角）与三个轴之间的关系如上图所示：

\[ \begin{aligned} &\beta = arcsin(\frac{a_x}{g}) \\ &\gamma = arcsin(\frac{a_y}{g}) \end{aligned} \]

其中重力加速度 $ g $ 的取值使用三轴角速度的矢量和即：

\[ g = \sqrt{a_x^{2} + a_y^{2} + a_z^{2}} \]

将 g 的值带入上式可以得到：

\[ \begin{aligned} &\beta = arctan(\frac{a_x}{\sqrt{a_y^{2} + a_z^{2}}}) \\ &\gamma = arctan(\frac{a_y}{\sqrt{a_x^{2} + a_z^{2}}}) \end{aligned} \]

其中 α 为俯仰角 pitch，β 为滚转角 roll，其中航向角 yaw 是没有办法通过加速度计来计算的。

openwrt 编译错误

you should not run configure as root (set FORCE_UNSAFE_CONFIGURE=1 in environment to bypass this check)

解决方法：

1

export FORCE_UNSAFE_CONFIGURE=1

Buildroot 配置

交叉编译工具链

Buildroot 为交叉编译工具链提供两种解决方案：

• 内部工具链后端，在配置界面中调用“Buildroot toolchain”
• 外部工具链后端，在配置界面中调用“External toolchain“；有三种方式来使用外部工具链：
  • 让 Buildroot 基于预定义的外部工具链 profile 自动下载、安装。在 Toolchain 中选择已有的 profile 即可
  • 为 Buildroot 手动指定提前安装好的、预定义了 profile 的工具链。在 Toolchain 中选择 profile 后，反选掉 Download toolchain automatically 并在 Toolchain path 中填写已有工具链路径即可
  • 使用定制的外部工具链。通常用于使用 crosstool-NG 或 Buildroot 生成的已有定制工具链。选择 Toolchain 列表中的 Custom toolchain ，然后填写 Toolchain path, Toolchain prefix, External toolchain C librrary 选项。若外部工具链使用 glibc 库，只需要选择工具链是否支持 C++ 以及是否内建 RPC 支持即可。如果使用 uClibc 库，则还有宽字符、本地化、程序 invocation、线程支持等选项

Buildroot 不支持由 OpenEmbedded、Yocto 支持的工具链，因为这些工具生成的工具链并不是单纯的工具链——它们除了编译器、binutils、C/C++ 库之外还加了一大堆预编译的库和程序。因此 Buildroot 并没有办法导入它们的 sysroot 。Buildroot 也不支持发行版提供的工具链，这些工具链包含的东西也比较复杂，所以无法加载到构建环境中。

何为实时性？

RTOS 的实时性该怎么理解呢？快速？确定性？

从中断控制器视角看实时性

我们知道一般都是 Cortex-M 跑 RTOS，Cortex-A 很少跑 RTOS，一般都是跑 Linux、Android 这些非实时系统。如果单纯从速度来看 A 核在高主频加持下一定会具有更快的速度才对呀，那 M 核的竞争力在哪里呢？实际上这就是 A 核和 M 核在设计上的两个不同方向的取舍。

首先我们看 NVIC 中断控制器的设计：

• 中断延迟波动很小：NVIC 支持中断嵌套，这样即使当前中断在处理中且非常耗时也没关系，因为可以通过高优先级的中断来响应更紧急的事件，这样中断延迟就不依赖与中断处理时间了，从设计上保证了延迟的确定性。
• 中断延迟小：NVIC 在不同的中断会跳转到不同地址运行，且可以直接在硬中断上下文中执行中断程序，这样整个 pipeline 很短，且 NVIC 还支持尾链这个概念进一步降低延迟（当高优先级的 ISR 抢占低优先级 ISR 时，处理器会跳过上下文保存和恢复，直接处理第二个 ISR，没有任何额外的开销）。通常 NVIC 中断响应时间在十几到几十 ns 之间。

NVIC 中断控制器在实时性上是满足要求的，快速和确定性都满足，但是他不适合处理大量中断，假如每秒要处理成千上万（这个中断数量对于 A 核来讲是很常见的 UAC、UVC，DSP 等一个模块每秒可能就有几千个中断）个中断，那么对 NVIC 来讲这是灾难性的，各种嵌套设计各种性能评估，除此之外对于多核系统 NVIC 也没有一套将中断分配给各个 CPU 核的机制，那么就无法充分利用多核的优势提高中断处理能力。而 A 核的 GIC 控制器就是为解决这些问题而设计的。

Cortex-A 核的 GIC 中断控制器设计很复杂，但是不支持中断嵌套，由 Distributor、CPU interface、Redistributor、ITS 组成，Distributor 具有仲裁和分发的作用，会将中断发送给 Redistributor，Redistributor 将中断发送给 CPU interface。这样第一解决了多核问题，其次 GIC 没有中断嵌套，当中断发生后跳转到一个固定地址，然后判断中断源进行下一步跳转，在 Linux 中接下来就会分为中断上半部和下半部机制，上半部在硬中断上下文快速响应然后返回，以更快处理其他中断兼顾实时性。中断下半部为了不同的应用需求设计了 softirq、tasklet、workqueue、thread 等机制来实现大量的中断任务，兼顾高性能。GIC 中断控制器解决了 NVIC 的问题但是却丢了硬实时性。

• 中断延迟比较大：中断处理的 PipeLine 比较长，中断响应延迟一般在 us 级别。
• 中断延迟波动比较大：中断不支持嵌套那么就一定要等上一个中断返回才能得到处理，这个延迟就不可控了。

从中断控制器视角看实时性是快速+确定的 latency。

获取 ns 时间戳（已弃用）

1
2
3
4
5
6
7

#include <linux/timekeeping32.h>

struct timespec ts;
u64 ns;

getnstimeofday(&ts);
ns = timespec_to_ns(&ts);

ktime accessors — The Linux Kernel documentation

可以使用 ktime_get_ns() 替代。 如果要获取 us 时间会涉及到 64bit 除法问题，会遇到如下问题：

1

ERROR: modpost: "__aeabi_uldivmod" [common_drivers/drivers/usb/dwc_otg.ko] undefined!

调用 div_u64() 函数，需要 include <linux/math64.h>

1

u64	tm = div_u64(ktime_get_raw_ns(),1000);

基本使用

设置开机自启动并启动 Docker-CE

1
2

sudo systemctl enable docker
sudo systemctl start docker

C Tips

区别以下函数

1
2
3
4
5
6
7

int* f();        //f 为一个函数，函数返回值为指向整形的指针
int (*f)();      //f 为一个指针，该指针指向一个函数
int* f[];        //f 为一个数组，数组内容为指针
int (*f[])();    //f 为数组，数组的内容为指向函数的指针
int*(*f[])();    //f 为数组，数组的内容为指向函数的指针，该函数返回一个指向整形的指针
int f()[];       //不存在
int f[]();       //不存在