修改UAC配置参数后无法正常通信

如果修改了UAC的配置后出现UAC无法正常通信的问题，可以通过修改设备的idVendor和idProduct来解决，只有设备的idVendor和idProduct发生改变Windows才会重新读取设备的配置描述符。

USB sof统计方法

打时间戳方式

1. ktime_get_raw_ns() Linux标准接口。
2. meson_timestamp() Amlogic实现的硬件定时器接口。

sof打时间戳的时机

1. 直接在SOF中断handle里打时间戳，然后将其保存到一个fifo里。
2. 通过一个hrtimer，主动查询SOF中断寄存器查看是否有SOF包，如果有SOF包则打上时间戳保存到fifo里。

sof时间戳导出到应用层

通过seq file创建一个proc（/proc/sof_ts）文件，应用通过读取该文件来获取sof时间戳。

buffer 统计

采样间隔 1ms、采样 buffer 里的数据长度

😊 There are two types of DMA mappings

Consistent DM（硬件保证 cache 一致性） mappings which are usually mapped at driver initialization, unmapped at the end and for which the hardware should guarantee that the device and the CPU can access the data in parallel and will see updates made by each other without any explicit software flushing.

Streaming DMA（需要软件来维护 cache 一致性） mappings which are usually mapped for one DMA transfer, unmapped right after it (unless you use dma_sync_* below) and for which hardware can optimize for sequential accesses.

Memory Mapped IO

Getting Access to the Device

This address should not be used directly. Instead, to get an address suitable for passing to the accessor functions described below, you should call ioremap(). An address suitable for accessing the device will be returned to you.

After you've finished using the device (say, in your module's exit routine), call iounmap() in order to return the address space to the kernel. Most architectures allocate new address space each time you call ioremap(), and they can run out unless you call iounmap().

同步问题原因

USB Isochronous 传输（协议无问题）

Isochronous Transfer 同步问题

电脑播放器播放音乐时：是按一个固定的速率，比如 44.1KHZ，电脑内有一个晶振，可分频出一个 44.1KHZ，进行音乐播放，发给 USB 的数据流速率固定。USB 声卡自己得有一个晶振才能工作，它也可分频出一个 44.1KHZ，供给 I2S 信号或 DAC。

问题来了，晶振是有误差的，这两个 44.1KHZ 不可能完全一模一样，电脑可能是 44.100KHZ，USB 声卡可能是 44.098KHZ，误差约 50ppm，很正常的情况。虽然声卡晶振分频出来是 44.098KHZ，但声卡认为它就是工作在 44.100KHZ 下。好吧，如果二者时钟独立运行，那么 1 个小时会误差 0.2 秒，会出现不同步！ 即电脑播了 1 个小时的数据，USB 声卡实际是无法播完的，要多 0.2 秒才能播完。 如果声卡也要 1 小时播完，那这 1 小时就需要丢掉 0.2 秒的数据。

所以二者的时钟必须要同步一致才行，这就是 UAC 同步问题的原因，因此 USB 音频规定了一是采用“等时传输模式”，二是设备需要指定为 3 种同步方式之一：同步（synchronous），适应（adaptive），异步（asynchronous）。

音量基本概念

声学中的分贝

因为人耳的特性，我们对声音的大小感知呈对数关系。所以我们通常用分贝描述声音大小，分贝（decibel）是量度两个相同单位之数量比例的单位，主要用于度量声音强度，常用 dB 表示。声学中，声音的强度定义为声压。计算分贝值时采用 20 微帕斯卡为参考值（通常被认为是人类的最少听觉响应值，大约是 3 米以外飞行的蚊子声音）。这一参考值是人类对声音能够感知的 阈值 下限。声压是场量，因此使用声压计算分贝时使用下述版本的公式：

\[ L_p = 20log_{10}(\frac{p_{rms}}{p_{ref}})dB \]

其中的 pref 是标准参考声压值 20 微帕。

分贝声音变化范围

在编程中，我们可以用以下公式计算两个声音之间的动态范围，单位为分贝：

\[ dB = 20 * log(A1 / A2) \]

其中 A1 和 A2 是两个声音的振幅，在程序中表示每个声音样本的大小。声音采样大小（也就是量化深度）为 1bit 时，动态范围为 0，因为只可能有一个振幅。采样大小为 8bit 也就是一个字节时，最大振幅是最小振幅的 256 倍。因此，动态范围是 48 分贝，计算公式如下：

\[ dB = 20 * log(256) \]

48 分贝的动态范围大约是一个安静房间和一台运行着电动割草机之间的区别。如果将声音采样大小增加一倍到 16bit，产生的动态范围则为 96 分贝，计算公式如下：

\[ dB = 20 * log(65536) \]

这非常接近听力最低阈值和产生痛感之间的区别，这个范围被认为非常适合还原音乐。

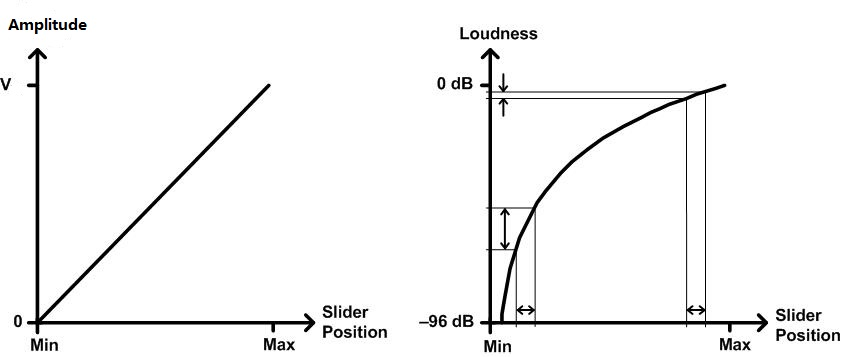
音量滑块与声音增幅大小线性变化

HID 相关概念

报表描述符由描述 HID 设备的数据项目（Item）组成，Item 的第一个字节（项目前缀）由三部分构成，即项目类型（item type）、项目标签（item tag）和项目长度（item size）。

HID 的项目有短项目和长项目两种，其中短项目的格式如下图：

Interrupts

中断用于通知 host 音频功能的当前状态发生了变化。本规范目前定义了两种不同类型的中断：

• Memory Change: 某些内部实体的内存位置已更新。可以通知主机软件，以便采取适当的行动。
• Control Change: 音频函数内部的某些可寻址控件更改了其一个或多个属性值

时钟实体、单元或终端内部的音频控件可以是中断的源。同样，AudioControl 接口中的任何可寻址 Control 或任何 AudioStreaming 接口都可以生成中断。最后所有与音频端点相关的可寻址控件都可能是中断的源。

音频功能的状态变化通常是由发生的特定事件引起的。事件可以是用户发起的，也可以是设备发起的。用户发起的插孔插入或移除是用户发起事件的典型示例。主机可以切换选择器或混音器，以便从刚刚插入的设备 （例如耳机）播放音频，并停止从当前设备（例如扬声器） 播放音频。设备启动事件的示例如下：一个外部设备 （例如 A/V 接收器可以在其光学数字输出上从 PCM 转换为 AC-3 编码数据，这取决于当前正在播放的材料如果此设备连接到具有自动检测功能的音频功能的光学数字输入，则该音频功能上的接口可能需要重新配置（例如，启动 AC-3 解码过程），这可能会导致所有其他接口的格式发生某些变化，甚至变得不可用。设备可以发出中断，让主机知道音频功能需要重新配置。

Standard Requests

音频设备类支持 USB 规范的第 9 节“USB 设备框架”中描述的标准请求。音频设备类对标准请求的值没有提出特定的要求。

Class-Specific Requests

特定于类的请求用于设置和获取与音频相关的控件。这些控制器主要分为两组：那些操纵音频功能的控制器，如音量，音调，选择器的位置等。以及那些影响等时终点上的数据传输的数据，比如当前的采样频率。

• AudioControl Requests

  对音频功能的控制是通过操作嵌入在音频功能的实体中的单个控件的属性来执行的。特定于类的音频控件接口描述符包含一组实体描述符，每个描述符指示实体中存在哪些控件。音频控制请求总是指向音频功能的单个音频控制接口。请求包含足够的信息（实体 ID、控制选择器和通道号），以便音频功能决定必须路由特定请求的位置。同样的请求布局也可用于特定于供应商的对扩展单元的请求。但是，本规范不包括它们

• AudioStreaming Requests

  对音频流接口的类特定行为的控制是通过操作接口控制或端点控制来执行的。它们可以是特定于类的（如本规范中定义的）或特定于供应商的。对于任何一种情况，都可以使用相同的请求布局。音频流请求被定向到控件所在的收件人。这可以是接口或它关联的等时端点。

音频设备类支持一个附加的特定于类的请求：

• Memory Requests

  音频功能中的每个可寻址实体（时钟实体、终端、单元、接口和端点）都可以公开一个内存映射接口，从而提供通用地操作实体的方法。特定于供应商的控制实现可以基于这种类型的请求。

原则上，所有的请求都是可选的。如果音频功能不支持某个请求，则必须通过在向该功能发出请求时停止控制管道来表明这一点。但是，如果支持某个集合请求，则也必须支持关联的 Get 请求。可以支持获取请求，而不支持关联的集合请求。如果支持中断，那么就必须实现所有必要的 Get 请求，这些请求需要从音频功能中检索适当的信息，以响应这些中断