微积分（下）

原图

多元函数微分

多元函数及其邻域

二元函数的严格定义： 假设\(D\)是二维向量\((x,y)\)的集合，\(D\)上的二元函数\(\ f\)是一个映射法则，它对\(D\)内的每一个有序对\((x,y)\)指定唯一的一个实数：

\[ z=f(x,y),\quad (x,y)\in D \]

如果用\(P\)来代替\((x,y)\)的话，也可以写作：

\[ z=f(P),\quad P\in D \]

\(D\)称为\(f\)的定义域，\(x、y\)（或\((x,y)\)，或\(P\)）称为\(f\)的自变量，\(z\)称为\(f\)的因变量。

如果定义域\(D\)是更高维的向量的集合，也就是说自变量为更高维的向量，那么 \(f\)可以称为多元函数，也叫作多变量函数。

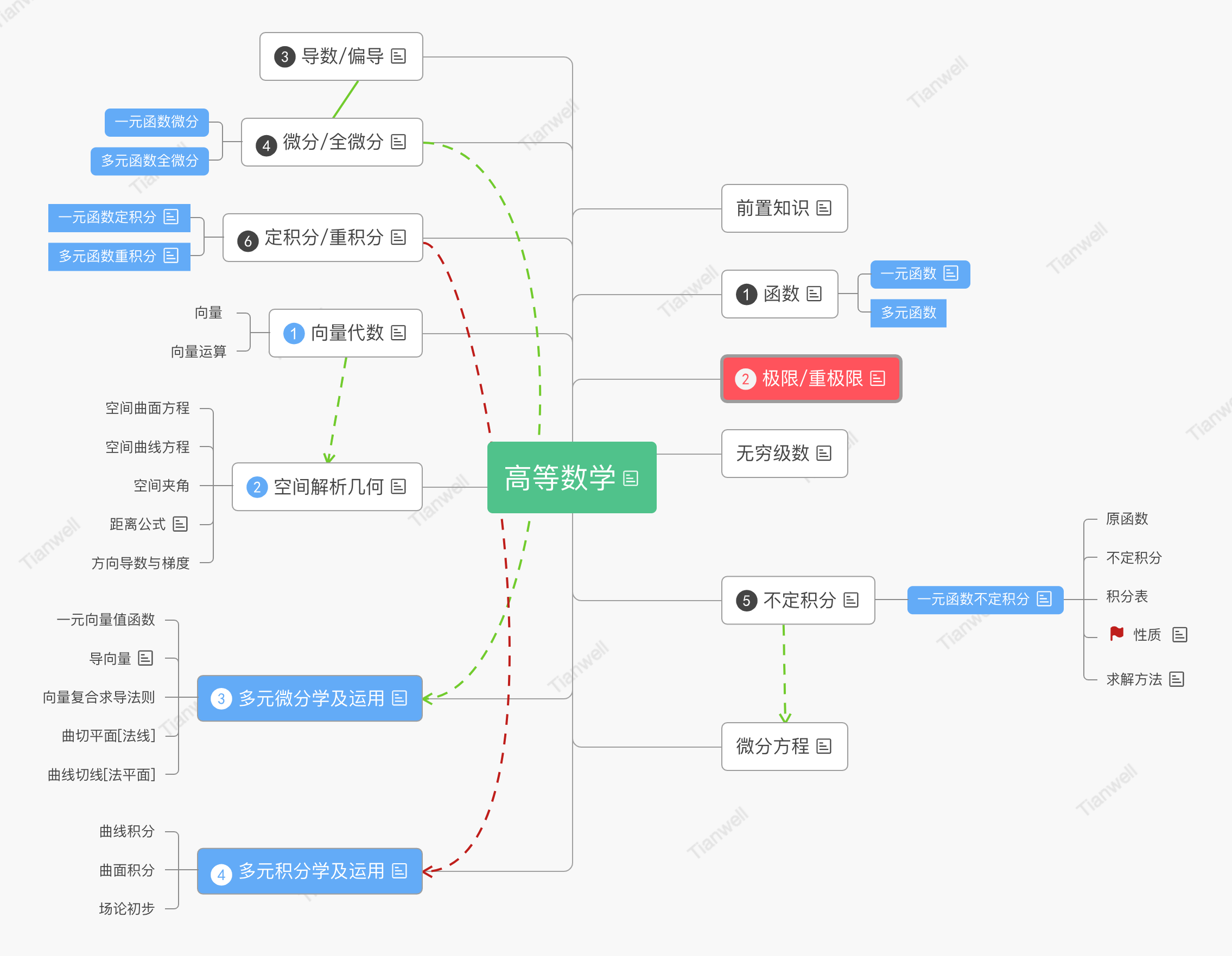
邻域和去心邻域：

二维向量的邻域要比一维向量的复杂。对于二维向量\(P_0(x_0,y_0)\)而言，半径为\(\delta\) 邻域可以表示为平面点集：

\[ U(P_0,\delta)=\{(x,y)\ |\ (x-x_0)^2 + (y-y_0)^2 < \delta^2\} \]

多元函数极限和连续

• 聚点： 如果对于任意给定的\(\delta > 0\)，点\(P\)的去心邻域\(\mathring{U}(P,\delta)\)内总有平面点集\(E\)中的点，那么称点\(P\)为\(E\)的聚点。 定义聚点是为了保证，从\(P_0(x_0,y_0)\)的某去心邻域内的某一点\(P(x,y)\)出发，至少能找到一串完全在 E 中的点来靠近\(P_0\)

• 二元函数极限的定义： 设二元函数\(f(x,y)\)的定义域为\(D，P_0(x_0,y_0)\)是\(D\)的聚点。如果存在常数\(L\)，对于任意给定的正数\(\epsilon\)，总存在正数\(\delta\)，使得当点\(P(x,y)\)满足下列条件时： \[ (x,y)\in D\cap \mathring{U}(P_0,\delta) \] 都有： \[ |f(x,y)-L| < \epsilon \] 成立，那么就称常数\(L\)为函数\(f(x,y)\)当\((x,y)\to(x_0,y_0)\)时的极限，记作： \[ \lim_{(x,y)\to(x_0,y_0)}f(x,y)=L\quad 或、quad f(x,y)\to L\ \big(\ (x,y)\to(x_0,y_0)\ \big) \] 因为这是二元函数的极限，所以也称作二重极限。

• 连续： 设二元函数\(f(x,y)\)的定义域为\(D\)，\(P_0(x_0,y_0)\)是\(D\)的聚点，且\(P_0\in D\)，如果： \[ \lim_{(x,y)\to(x_0,y_0)}f(x,y)=f(x_0,y_0) \] 那么称函数\(f(x,y)\)在点\(P_0(x_0,y_0)\)连续。

全微分

设函数\(z=f(x,y)\)在点\((x_0,y_0)\)的某邻域内有定义，假设：

\[ \Delta x=x-x_0,\quad \Delta y=y-y_0 \]

如果函数\(z=f(x,y)\)在点\((x_0,y_0)\)的全增量：

\[ \Delta z=f(x_0+\Delta x, y_0+\Delta y)-f(x_0, y_0) \]

可以表示为：

\[ \Delta z=A\Delta x+B\Delta y+o(\rho)=A\Delta x+B\Delta y+\epsilon_1\Delta x+\epsilon_2\Delta y \]

其中\(A、B\)不依赖于\(\Delta x、\Delta y\)，且：

\[ \rho=\sqrt{(\Delta x)^2+(\Delta y)^2},\quad \lim_{\Delta x\to 0}\epsilon_1=0,\quad \lim_{\Delta y\to 0}\epsilon_2=0 \]

那么称\(z=f(x,y)\)在点\((x_0,y_0)\)处可微分，而\(A\Delta x+B\Delta y\)称为\(z=f(x,y)\)在点\((x_0,y_0)\)处的全微分（或称为切平面），记作\(\mathrm{d}z\)，即：

\[ \mathrm{d}z=A\mathrm{d}x+B\mathrm{d}y \]

可以类比单变量微分的定义，单变量微积分是以直线代替曲线，双变量全微分是以平面代替曲线。

偏导数

• 关于\(x\)的偏导数： \[ \left.\frac{\partial f}{\partial x}\right|_{(x_0,y_0)}=\left.\frac{\mathrm{d}}{\mathrm{d}x}f(x,y_0)\right|_{x=x_0}=\lim_{h\to 0}\frac{f(x_0+h,y_0)-f(x_0,y_0)}{h} \]

• 关于\(y\)的偏导数： \[ \left.\frac{\partial f}{\partial y}\right|_{(x_0,y_0)}=\left.\frac{\mathrm{d}}{\mathrm{d}y}f(x_0,y)\right|_{y=y_0}=\lim_{h\to 0}\frac{f(x_0,y_0+h)-f(x_0,y_0)}{h} \]

• 与全微分的关系： 如果函数\(z=f(x,y)\)在点\((x_0,y_0)\)可微分，那么该函数在点\((x_0,y_0)\)的偏导数\(f_x(x_0,y_0)、f_y(x_0,y_0)\)必定存在，且\(z=f(x,y)\)在点\((x_0,y_0)\)的全微分为： \[ \mathrm{d}z=f_x(x_0,y_0)\mathrm{d}x+f_y(x_0,y_0)\mathrm{d}y \]

方向导数与梯度

对于二元函数\(z=f(x,y)\)，沿某单位向量：

\[ \boldsymbol{u}=\begin{pmatrix}u_1\\u_2\end{pmatrix} \]

在\((x_0,y_0)\)点的方向导数为：

\[ \left.\frac{\partial f}{\partial u}\right|_{(x_0,y_0)}=\lim_{t\to 0}\frac{f(x_0+tu_1, y_0+tu_2)-f(x_0,y_0)}{t},\quad t\in\mathbb{R} \]

单位向量还可以用该向量的方向余弦\(\cos\alpha\)和\(\cos\beta\)表示，即：

\[ \boldsymbol{u}=\begin{pmatrix}u_1\\u_2\end{pmatrix}=\begin{pmatrix}\cos\alpha\\\cos\beta\end{pmatrix} \]

所以方向导数也常表示为：

\[ \left.\frac{\partial f}{\partial u}\right|_{(x_0,y_0)}=\lim_{t\to 0}\frac{f(x_0+t\cos\alpha, y_0+t\cos\beta)-f(x_0,y_0)}{t},\quad t\in\mathbb{R} \]

• 模长：该方向向量的模长是方向导数的最大值。
• 方向：该方向向量的方向正是取得最大方向导数的方向。
• 投影：它向某单位向量\(\boldsymbol{u}\)的投影就是对应的方向导数。

该方向向量就称为梯度，记作：

\[ \nabla f(x_0,y_0)=grad f(x_0,y_0)=\begin{pmatrix}f_x(x_0,y_0)\\f_y(x_0,y_0)\end{pmatrix}=f_x(x_0,y_0)\boldsymbol{i}+f_y(x_0,y_0)\boldsymbol{j} \]

直观的理解就是：

• 沿着梯度向量方向走，能以最快的速度到达山顶。
• 逆着梯度向量方向走，能以最快的速度到达山脚。
• 和梯度向量方向垂直，此时坡度为 0，即不上山也不下山。

全导数

若\(z=f(x,y)\)是可微分的，而 x 和 y 是 t 的可导函数，则 z 是 t 的可导函数，并且：

\[ \frac{\mathrm{d}z}{\mathrm{d}t}=\frac{\partial z}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}t}+\frac{\partial z}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}t} \]

这个导数可以看作过切点的曲线的导数，所以又被称为全导数。

总结： \[ \begin{array}{c|c} \hline \quad \quad&\quad 描述、quad &\quad 公式 \quad\\ \hline \\ \quad 偏导数 \quad&\quad \begin{aligned}y=y_0\ 和、x=x_0\ 两平面、\ \\与曲面相交所得曲线的导数、end{aligned}\quad&\quad f_x=\frac{\partial f}{\partial x},f_y=\frac{\partial f}{\partial y}\quad \\ \\ \hline \\ \quad 方向导数 \quad&\quad\begin{aligned}垂直于 xy 的平面、quad\quad\ \ \\与曲面相交所得曲线的导数、\ \end{aligned}\quad&\quad \frac{\partial f}{\partial u}=f_x\cos\alpha+f_y\cos\beta\quad\\ \\ \hline \\ \quad 全导数 \quad&\quad\begin{aligned}垂直于 xy 的曲面、quad\quad\ \ \\与曲面相交所得曲线的导数、\ \end{aligned}\quad&\quad\frac{\mathrm{d}z}{\mathrm{d}t}=\frac{\partial z}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}t}+\frac{\partial z}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}t}\quad\\ \\ \hline \end{array} \]

雅可比矩阵

• 二元函数的导数： 二元函数\(z=f(x,y)\)的微分，微分在\(\mathrm{d}x\mathrm{d}y\mathrm {d}z\)坐标系中的方程为：

  \[ \mathrm{d}z=f_x\mathrm{d}x+f_y\mathrm{d}y \]

  可以改写为矩阵的形式： \[ \underbrace{\begin{pmatrix}\mathrm{d}z\end{pmatrix}}_ {\boldsymbol{d_z}}\quad=\quad\underbrace{\begin{pmatrix} f_x&f_y\end{pmatrix}}_{T}\quad\underbrace{\begin{pmatrix} \mathrm{d}x\\\mathrm{d}y\end{pmatrix}}_{\boldsymbol{d_{xy} }} \]

  或者写作：

  \[ \boldsymbol{d_z}=T\boldsymbol{d_{xy}} \]

• 一般的多元函数： \[ y=f(x_1,x_2,\cdots,x_n),\quad (y,x_1,x_2,\cdots, x_n\in\mathbb{R}) \]

  如果可微的话，那么微分方程为：

  \[ \mathrm{d}y=f_{x_1}\mathrm{d}x_1+f_{x_2}\mathrm{d}x_2 +\cdots+f_{x_n}\mathrm{d}x_n \]

  可以改写为矩阵的形式：

  \[ \underbrace{\begin{pmatrix}\mathrm{d}y\end{pmatrix}}_ {\boldsymbol{d_y}}\quad=\quad\underbrace{\begin{pmatrix}f_ {x_1}&f_{x_2}&\cdots&f_{x_n}\end{pmatrix}}_{T} \quad\underbrace{\begin{pmatrix}\mathrm{d}x_1\\\mathrm{d} x_2\\\vdots\\\mathrm{d}x_b\end{pmatrix}}_{\boldsymbol{d_ {x}}} \]

  或者写作：

  \[ \boldsymbol{d_y}=T\boldsymbol{d_{x}} \]

  其中矩阵 T 就是该多元函数的导数。

• 二元方程组的导数： \[ \begin{cases} \mathrm{d}z=\frac{\partial f}{\partial x}\mathrm{d}x +\frac{\partial f}{\partial y}\mathrm{d}y\\ \\ \mathrm{d}w=\frac{\partial g}{\partial x}\mathrm{d}x +\frac{\partial g}{\partial y}\mathrm{d}y \end{cases} \] 可以写成矩阵的形式： \[ \underbrace{\begin{pmatrix}\mathrm{d}z\\\mathrm{d}w\end{pmatrix}}_{\boldsymbol{d_{v}}}\quad=\quad\underbrace{\begin{pmatrix}\frac{\partial f}{\partial x}&\frac{\partial f}{\partial y}\\\frac{\partial g}{\partial x}&\frac{\partial g}{\partial y}\end{pmatrix}}_{T}\quad\underbrace{\begin{pmatrix}\mathrm{d}x\\\mathrm{d}y\end{pmatrix}}_{\boldsymbol{d_{u}}} \] 或者写作： \[ \boldsymbol{d_{v}}=T\boldsymbol{d_{u}} \] 其中矩阵 T 就是该方程组所代表的函数的导数。

• 雅可比矩阵（多元方程组的导数矩阵）： 假如\(f_1,f_2,\cdots,f_n\)都是\(x_1,x_2,\cdots,x_m\)的函数，并且相对于各个自变量的偏微分都存在，那么定义 T 为： \[ T=\frac{\partial (f_1,f_2,\cdots,f_n)}{\partial (x_1,x_2,\cdots,x_m)}=\begin{pmatrix}\frac{\partial f_1}{\partial x_1}&\frac{\partial f_1}{\partial x_2}&\cdots&\frac{\partial f_1}{\partial x_m}\\\frac{\partial f_2}{\partial x_1}&\frac{\partial f_2}{\partial x_2}&\cdots&\frac{\partial f_2}{\partial x_m}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial f_n}{\partial x_1}&\frac{\partial f_n}{\partial x_2}&\cdots&\frac{\partial f_n}{\partial x_m}\end{pmatrix} \] 该矩阵\(T\)称为雅可比矩阵。因为雅可比矩阵的英文名为 Jacobian Matrix，所以上述矩阵又常写作： \[ J=\frac{\partial (f_1,f_2,\cdots,f_n)}{\partial (x_1,x_2,\cdots,x_m)} \]

• 海森矩阵： 一元导数\(y=f(x)\)的二阶导数就是连续两次使用\(\frac{\mathrm{d}}{\mathrm{d}x}\)： \[ \frac{\mathrm{d}^2y}{\mathrm{d}x^2}=\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right) \] 类似的，二元函数\(z=f(x,y)\)的二阶导数就是连续两次计算雅可比矩阵： \[ \frac{\partial^2 z}{\partial(x,y)^2}=\frac{\partial }{\partial(x,y)}\left(\frac{\partial z}{\partial(x,y)}\right)=\begin{pmatrix}f_{xx}&f_{xy}\\f_{yx}&f_{yy}\end{pmatrix} \] 二阶导数又称为海森矩阵（Hessian Matrix），所以常用 H 来表示这个矩阵： \[ H=\frac{\partial^2 z}{\partial(x,y)^2}=\begin{pmatrix}f_{xx}&f_{xy}\\f_{yx}&f_{yy}\end{pmatrix} \] 海森矩阵可以判断图像的凹凸性。

此外关于隐函数的求导，多元函数的极值求法这里不再列出，详细可以参考相关书籍。

重积分

二重积分

设\(f(x,y)\)是有界闭区域\(D\)上的有界函数，将闭区域\(D\)任意分成\(n\)个小闭区域：

\[ \Delta A_1,\Delta A_2,\cdots,\Delta A_i,\cdots,\Delta A_n \]

其中\(\Delta A_i\)表示第\(i\)个小闭区域，也表示它的面积，规定\(\Delta A_i\)中最长的直径（一个闭区域的直径是指区域上任意两点间距离的最大者）为\(\lambda\)，在每个\(\Delta A_i\)内任取一点\((x_i,y_i)\)，可以得到级数：

\[ \sum_{i=0}^{n}f(x_i,y_i)\Delta A_i \]

如果当\(\lambda\to 0\)时，无论如何划分闭区域\(D\)，无论怎样选取\((x_i,y_i)\)，该级数的极限总是存在，那么称此极限为函数\(f(x,y)\)在闭区域\(D\)上的二重积分，记作：

\[ \iint_{D} f(x, y) \mathrm{d} A=\lim _{\lambda \rightarrow 0} \sum_{i=0}^{n} f\left(x_{i}, y_{i}\right) \Delta A_{i} \]

其中\(f(x,y)\)称为被积函数，\(\mathrm{d}A\)称为面积微分，\(x\)与\(y\)称为积分变量，\(D\)称为积分区域。

二重积分的性质

设\(f(x,y)，g(x,y)\)都是有界闭区域\(D\)上的有界函数，\(\alpha、\beta\)为常数，则：

• 齐次性： \[ \iint_{D} \alpha f(x, y) \mathrm{d} A=\alpha \iint_{D} f(x, y) \mathrm{d} A \]

• 可加性： \[ \iint_{D}(f(x, y)+g(x, y)) \mathrm{d} A=\iint_{D} f(x, y) \mathrm{d} A+\iint_{D} g(x, y) \mathrm{d} A \]

• 推论： \[ \iint_{D}(\alpha f(x, y) \pm \beta g(x, y)) \mathrm{d} A=\alpha \iint_{D} f(x, y) \mathrm{d} A \pm \beta \iint_{D} g(x, y) \mathrm{d} A \]

• 区域可加性： 如果闭区域\(D\)被有限条曲线分为有限个部分闭区域，那么\(D\)上的二重积分等于各部分闭区域上的二重积分之和。

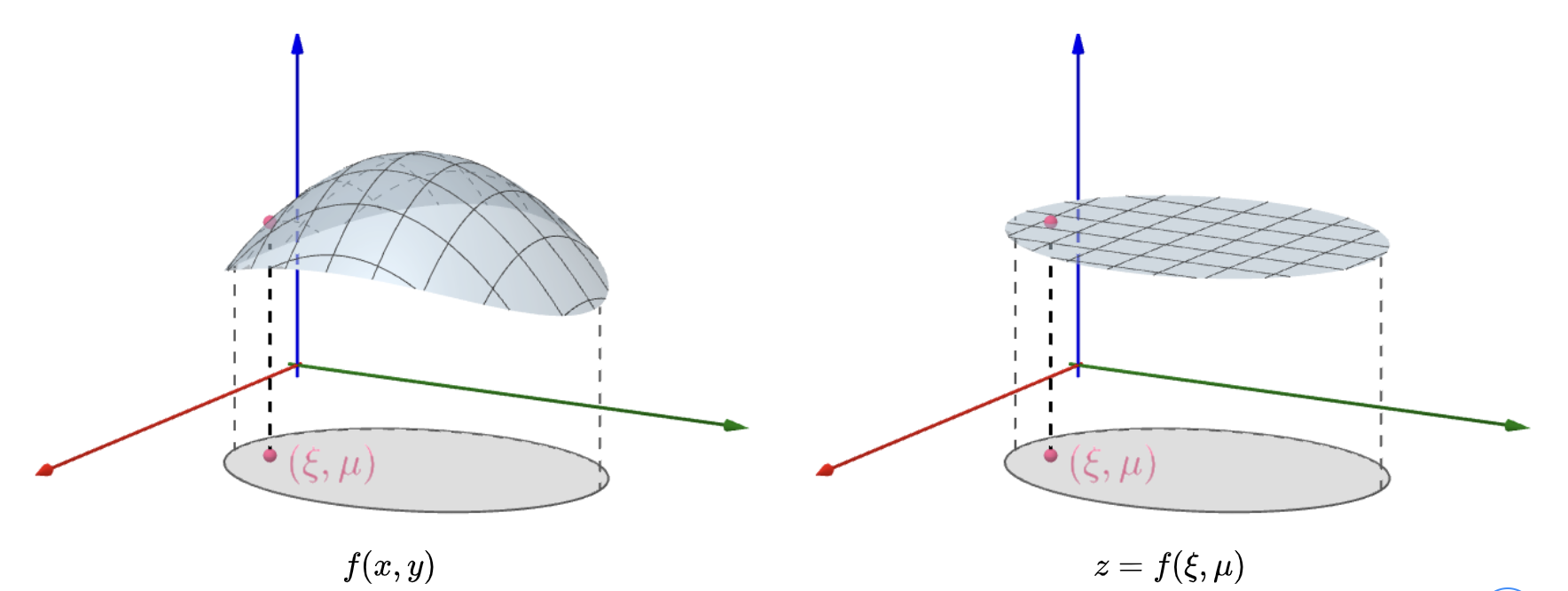
• 二重积分中值定理： 设函数\(f(x,y)\)在闭区域\(D\)上连续，\(A\)是区域\(D\)的面积，则在\(D\)上至少存在一点\((\xi,\mu)\)，使得： \[ \iint_{D} f(x, y) \mathrm{d} A=f(\xi, \mu) A \]

二重积分法

弱富比尼定理

设有矩形区域\(R\)：

\[ R=\{(x,y)|a\le x\le b,c\le y\le d\} \]

若\(f(x,y)\)在区域\(R\)上连续，则：

\[ \iint_{R} f(x, y) \mathrm{d} A=\int_{c}^{d}\left[\int_{a}^{b} f(x, y) \mathrm{d} x\right] \mathrm{d} y=\int_{a}^{b}\left[\int_{c}^{d} f(x, y) \mathrm{d} y\right] \mathrm{d} x \]

将二重积分变为，先积 x 后积 y（或先积 y 后积 x）的二次积分。

强富比尼定理

若\(f(x,y)\)在区域\(D\)上连续：

• 若区域 D 为\(a \le x \le b, g_1(x) \le y \le g_2(x)\)，其中\(g_1、g_2\)在\([a,b]\)上连续，则：

\[ \iint_{D} f(x, y) \mathrm{d} A=\int_{a}^{b}\left[\int_{g_{1}(x)}^{g_{2}(x)} f(x, y) \mathrm{d} y\right] \mathrm{d} x \]

• 若区域 D 为\(c \le y \le d, h_1(y) \le x \le h_2(y)\)，其中\(h_1、h_2\)在\([c,d]\)上连续，则：

\[ \iint_{D} f(x, y) \mathrm{d} A=\int_{c}^{d}\left[\int_{h_{1}(y)}^{h_{2}(y)} f(x, y) \mathrm{d} x\right] \mathrm{d} y \]

可见，和富比尼定理的较弱形式不一样，这里是不能交换积分顺序的。

坐标系变换

有时候切换一下坐标系问题会变得简单的多，为此研究在坐标变换后的多重积分也是很有价值的。

在区域 D 上，如果\(xy\)直角坐标系和\(uv\)直角坐标系之间存在如下的坐标变换函数，且\(x(u,v)、y(u,v)\)在区域 D 上有一阶连续偏导数（这是为了保证可以找到最佳线性近似）：

\[ \begin{cases} x=x(u,v)\\ y=y(u,v) \end{cases} \]

如果雅可比行列式存在且不为 0：

\[ |J|=|\frac{\partial(x,y)}{\partial(u,v)}|=\begin{vmatrix}\frac{\partial x}{\partial u }&\frac{\partial x}{\partial v}\\\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}\end{vmatrix}\ne 0 \]

则区域 D 上在\(xy\)直角坐标系下的面积为：

\[ \iint_{D} \mathrm{~d} x \mathrm{~d} y=\iint_{D}\|J\| \mathrm{d} u \mathrm{~d} v \]

所以，\(z=f(x,y)\)在区域 D 上的体积为（在\(xyz\)直角坐标系下的体积）：

\[ \iint_{D} f(x, y) \mathrm{d} x \mathrm{~d} y=\iint_{D} f(x(u, v), y(u, v))\|J\| \mathrm{d} u \mathrm{~d} v \]

三重积分

设\(f(x,y,z)\)是有界闭区域\(\Omega\)上的有界函数，将闭区域\(\Omega\)任意分成\(n\)个小闭区域：

\[ \Delta V_1,\Delta V_2,\cdots,\Delta V_i,\cdots,\Delta V_n \]

其中\(\Delta V_i\)表示第\(i\)个小闭区域，也表示它的体积，规定\(\Delta V_i\)中最大的体积为\(\lambda\)：

\[ \lambda=\max(\Delta V_i) \]

在每个\(\Delta V_i\)内任取一点\((\xi_i,\mu_i,\zeta_i)\)，可以得到级数：

\[ \sum_{i=0}^{n}f(\xi_i,\mu_i,\zeta_i)\Delta V_i \]

如果当\(\lambda\to 0\)时，无论如何划分闭区域\(\Omega\)，无论怎样选取\((\xi_i,\mu_i,\zeta_i)\)，该级数的极限总是存在，那么称此极限为函数\(f(x,y,z)\)在闭区域\(\Omega\)上的三重积分，记作：

\[ \iiint_{\Omega} f(x, y, z) \mathrm{d} V=\lim _{\lambda \rightarrow 0} \sum_{i=0}^{n} f\left(\xi_{i}, \mu_{i}, \zeta_{i}\right) \Delta V_{i} \]

其中\(f(x,y,z)\)称为被积函数，\(\mathrm{d}V\)称为体积微分，\(x、y\)以及\(z\)称为积分变量，\(\Omega\)称为积分区域。

三重积分法

富比尼定理

区域 E 可以表示为： \[ E=\{(x,y,z)|a\le x\le b,g_1(x)\le y\le g_2(x), u_1(x,y)\le z\le u_2(x,y)\} \]

那么通过富比尼定理，函数\(f(x,y,z)\)在区域 E 上的三重积分可以如下计算：

\[ \begin{aligned} \iiint_{E} f(x, y, z) \mathrm{d} V &=\iint_{D}\left[\int_{u_{1}(x, y)}^{u_{2}(x, y)} f(x, y, z) \mathrm{d} z\right] \mathrm{d} A \\ &=\int_{a}^{b} \int_{g_{1}(x)}^{g_{2}(x)} \int_{u_{1}(x, y)}^{u_{2}(x, y)} f(x, y, z) \mathrm{d} z \mathrm{~d} y \mathrm{~d} x \end{aligned} \]

这样就将三重积分划为了方便计算的三次积分。

坐标系变换

同样变换坐标系是为了简化问题。这里直接给出坐标系变换积分公式：

• 柱面坐标系的体积微分： 通过雅可比行列式\(|J|\)，可得柱面坐标系函数\(w=f(\rho,\theta,z)\)在区域 \(\Omega\)上的三重积分为：

  \[ \begin{aligned} \iiint_{\Omega} f(\rho, \theta, z) \mathrm{d} V &=\iiint_ {\Omega} f(\rho, \theta, z)\|J\| \mathrm{d} \rho \mathrm{d} \theta \mathrm{d} z \\ &=\iiint_{\Omega} f(\rho, \theta, z) \rho \mathrm{d} \rho \mathrm{d} \theta \mathrm{d} z \end{aligned} \]

  其中\(\rho\mathrm{d}\rho\mathrm{d}\theta\mathrm{d}z\)称为柱面坐标系的 体积微分。

• 球面坐标系的体积微分： 通过雅可比行列式\(|J|\)，可得球面坐标系函数\(w=f(r,\varphi,\theta)\)在区域\(\Omega\)上的三重积分为： \[ \begin{aligned} \iiint_{\Omega} f(r, \varphi, \theta) \mathrm{d} V &=\iiint_ {\Omega} f(r, \varphi, \theta)\|J\| \mathrm{d} r \mathrm{~d} \varphi \mathrm{d} \theta \\ &=\iint_{\Omega} \iint(r, \varphi, \theta) r^{2} \sin \varphi \mathrm{d} r \mathrm{~d} \varphi \mathrm{d} \theta \end{aligned} \]

  其中\(r^2\sin\varphi\mathrm{d}r\mathrm{d}\varphi\mathrm{d}\theta\)称为球面坐标系的体积微分。

曲线积分与曲面积分

第一类曲线积分

设\(L\)为\(xOy\)面内的一条光滑曲线弧，函数\(f(x,y)\)在\(L\)上有界。在\(L\)上任意插入一点列\(P_0、P_1，\cdots、P_{n}\)，把\(L\)分成\(n\)个小段。设第\(k\)个小段的长度为\(\Delta s_k\)。又\((\xi_k,\eta_k)\)为第\(k\)个小段上任意取定的一点，做乘积\(f(\xi_k,\eta_k)\Delta s_k\)，并作和：

\[ \sum_{k=1}^{n}f(\xi_k,\eta_k)\Delta s_k \]

如果当各小弧段的长度的最大值\(\lambda\to 0\)时，这和的极限总是存在，且与曲线\(L\)的分法及点\((\xi_k,\eta_k)\)的取法无关，那么称此极限为函数\(f(x,y)\)在曲线\(L\)上的第一类曲线积分，记作：

\[ \int_L f(x,y)\mathrm{d}s=\lim_{\lambda\to 0}\sum_{k=1}^{n}f(\xi_k,\eta_k)\Delta s_k \]

其中\(\mathrm{d}s\)称为弧微分。

• 物理意义： 第一类曲线积分的物理意义还是很明显的，之前介绍过，如果\(\mu(x,y)\)是曲线\(L\)的密度函数时，如下计算的是曲线质量： \[ m=\int_L \mu(x,y)\mathrm{d}s \] 而如果\(\delta(x,y)\)是曲线\(L\)的电荷密度函数，那么如下计算的就是曲线的电荷量： \[ c=\int_L \delta(x,y)\mathrm{d}s \]

• 几何意义： 第一类曲线积分\(\int_L f(x,y)\mathrm{d}s\)的几何意义就是求曲线 L 与曲面\(z=f(x,y)\)之间的面积：

• 性质：

  • 性质 1：设\(\alpha、\beta\)为常数，则： \[ \int_L[\alpha f(x,y)+\beta g(x,y)]\mathrm{d}s=\alpha\int_L f(x,y)\mathrm{d}s+\beta\int_L g(x,y)\mathrm{d}s \]

  • 性质 2：设光滑曲线\(L\)可分为两个光滑曲线\(L_1\)和\(L_2\)，则： \[ \int_L f(x,y)\mathrm{d}s=\int_{L_1} f(x,y)\mathrm{d}s+\int_{L_2} f(x,y)\mathrm{d}s \]

  • 性质 3：设在光滑曲线 L 上有\(f(x,y)\le g(x,y)\)，则： \[ \int_L f(x,y)\mathrm{d}s\le\int_{L} g(x,y)\mathrm{d}s \]

第二类曲线积分

设\(L\)为\(xOy\)面内从\(A\)点到\(B\)点的一条光滑曲线弧，函数\(P(x,y)、Q(x,y)\)在\(L\)上有界。在\(L\)上任意插入一点列\(P_0、P_1，\cdots、P_{n}\)，把\(L\)分成\(n\)个有向小弧段：

\[ \overbrace{P_{k-1} P_{k}}, \quad\left(k=1,2, \cdots, n, P_{0}=A, P_{n}=B\right) \]

设\(\Delta x_k=x_k-x_{k-1}，\Delta y_k=y_k-y_{k-1}\)，点\((\xi_k,\eta_k)\)为\(\overbrace{P_{k-1} P_{k}}\)上任意取定的点，做乘积\(P(\xi_k,\eta_k)\Delta x_i\)，并作和：

\[ \sum_{k=1}^{n}P(\xi_k,\eta_k)\Delta x_k,\quad \sum_{k=1}^{n}Q(\xi_k,\eta_k)\Delta y_k \]

如果当各小弧段的长度的最大值\(\lambda\to 0\)时，和的极限总是存在，且与曲线\(L\)的分法及点\((\xi_k,\eta_k)\)的取法无关，就称这两个极限为\(P(x,y)\)在有向曲线\(\ L\) 上对坐标\(\ x\) 的曲线积分：

\[ \int_L P(x,y)\mathrm{d}x=\lim_{\lambda\to 0}\sum_{k=1}^{n}P(\xi_k,\eta_k)\Delta x_k \]

以及\(Q(x,y)\)在有向曲线\(\ L\) 上对坐标\(\ y\) 的曲线积分：

\[ \int_L Q(x,y)\mathrm{d}y=\lim_{\lambda\to 0}\sum_{k=1}^{n}Q(\xi_k,\eta_k)\Delta y_k \]

以上两个积分也称为第二类曲线积分。

• 性质：

  • 性质 1：设\(\alpha、\beta\)为常数，则： \[ \int_L[\alpha\boldsymbol{F_1}(x,y)+\beta\boldsymbol{F_2}(x,y)]\cdot\mathrm{d}\boldsymbol{s}=\alpha\int_L\boldsymbol{F_1}(x,y)\cdot\mathrm{d}\boldsymbol{s}+\beta\int_L\boldsymbol{F_2}(x,y)\cdot\mathrm{d}\boldsymbol{s} \]

  • 性质 2：设有向光滑曲线\(L\)可分为两个光滑有向曲线\(L_1\)和\(L_2\)，则： \[ \int_L \boldsymbol{F}(x,y)\cdot\mathrm{d}\boldsymbol{s}=\int_{L_1} \boldsymbol{F}(x,y)\cdot\mathrm{d}\boldsymbol{s}+\int_{L_2}\boldsymbol{F}(x,y)\cdot\mathrm{d}\boldsymbol{s} \]

  • 性质 3：设\(L\)是有向光滑曲线，\(L^-\)是\(L\)的反向曲线，则： \[ \int_L \boldsymbol{F}(x,y)\cdot\mathrm{d}\boldsymbol{s}=-\int_{L^-} \boldsymbol{F}(x,y)\cdot\mathrm{d}\boldsymbol{s} \]

两类曲线积分的关系

区别

• 第一类曲线积分针对的是曲线，而第二类曲线积分针对的是有向曲线。
• 第一类曲线积分，作用在曲线上的是标量；而第二类曲线积分，作用在曲线上的是向量。

联系

因为弧微分和有向弧微分的关系为\(\boldsymbol{\tau}\mathrm{d}s=\mathrm{d}\boldsymbol{s}\)，所以：

\[ \int_L \boldsymbol{F}\cdot\boldsymbol{\tau}\mathrm{d}s=\int_L \boldsymbol{F}\cdot\mathrm{d}\boldsymbol{s} \]

左边为第一类曲线积分，右边为第二类曲线积分，可见这两类积分是可以互相转化的。

二维的散度和旋度

通量

在连续向量场\(\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}\)中的光滑闭曲线\(L\)，\(\boldsymbol{n}\)为光滑闭曲线\(L\)的单位法向量（指向闭曲线外部），则\(\boldsymbol{F}\)穿过\(L\)的流量，即通量为：

\[ \oint_{L} \boldsymbol{F}\cdot\boldsymbol{n}\mathrm{d}s=\oint_{L}P\mathrm{d}y-Q\mathrm{d}x \]

需要注意的是，上式从第一类曲线积分变为了第二类曲线积分，曲线的方向为逆时针。

散度

已知水流量为向量场\(\boldsymbol{F}\)。用曲线\(L_A\)来表示 A 圆，那么 A 圆的通量为：

\[ T_A=\oint_{L_A} \boldsymbol{F}\cdot\boldsymbol{n}\mathrm{d}s \]

假设 A 圆对应的面积为\(\Omega_A\)，圆缩到最小即\(\Omega_A\to 0\)，同时再除上面积\(\Omega_A\)，就得到了\(A\)点在向量场\(\boldsymbol{F}\)中的通量密度，也称为 A 点在向量场\(\boldsymbol{F}\)中的散度，即：

\[ \operatorname{div}\boldsymbol{F}(A)=\lim_{\Omega_A\to 0}\frac{1}{\Omega_A}\oint_{L_A} \boldsymbol{F}\cdot\boldsymbol{n}\mathrm{d}s \]

同样的，也可以算出 C 点的散度\(\operatorname{div}\boldsymbol{F}(C)\)，两者谁大，就说明哪个水龙头的出水量更大。

环量

在连续向量场\(\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}\)中的光滑闭曲线\(L\)，\(\boldsymbol{\tau}\)为光滑闭曲线\(L\)的单位切向量\(\boldsymbol{\tau}\)（指向逆时针方向），则\(\boldsymbol{F}\)对于\(L\)的环量为：

\[ \oint_{L} \boldsymbol{F}\cdot\boldsymbol{\tau}\mathrm{d}s=\oint_{L}P\mathrm{d}x+Q\mathrm{d}y \]

需要注意的是，上式从第一类曲线积分变为了第二类曲线积分，曲线的方向为逆时针。

旋度

已知水流量为向量场\(\boldsymbol{F}\)。用曲线\(L_A\)来表示\(A\)圆，那么\(A\)圆的环量为：

\[ H_A=\oint_{L_A} \boldsymbol{F}\cdot\boldsymbol{\tau}\mathrm{d}s \]

可见，环量会受到圆的大小的影响，所以来排除掉这个影响。假设 A 圆对应的面积为\(\Omega_A\)，圆缩到最小即\(\Omega_A\to 0\)，同时再除上面积\(\Omega_A\)，就得到了\(A\)点在向量场\(\boldsymbol{F}\)中的环量密度，也称为\(A\)点在向量场\(\boldsymbol{F}\)中的旋度，即：

\[ \operatorname{curl}\boldsymbol{F}(A)=\lim_{\Omega_A\to 0}\frac{1}{\Omega_A}\oint_{L_A} \boldsymbol{F}\cdot\boldsymbol{\tau}\mathrm{d}s \]

格林公式

格林公式的通量形式：

某光滑闭曲线 L 围成闭区域 D，定义在闭区域 D 上的向量场\(\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}\)，它的分量具有一阶连续偏导数，则\(\boldsymbol{F}\)关于 L 的通量，可通过闭区域 D 上的散度求出：

\[ \underbrace{\oint_{L} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} s=\oint_{L} P \mathrm{~d} y-Q \mathrm{~d} x}_{\text {闭曲线的通量 }}=\underbrace{\iint_{D} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y} \mathrm{~d} x \mathrm{~d} y}_{\text {闭曲线围成区域的通量之和 }} \]

格林公式的环量形式：

某光滑闭曲线 L 围成闭区域 D，定义在闭区域 D 上的向量场\(\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}\)，它的分量具有一阶连续偏导数，则\(\boldsymbol{F}\)关于 L 的环量，可通过闭区域 D 上的旋度求出：

\[ \underbrace{\oint_{L} \boldsymbol{F} \cdot \boldsymbol{\tau} \mathrm{d} s=\oint_{L} P \mathrm{~d} x+Q \mathrm{~d} y}_{\text {闭曲线的环量 }}=\underbrace{\iint_{D} \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \mathrm{~d} x \mathrm{~d} y}_{\text {闭曲线围成区域的环量之和 }} \]

二重积分的基本定理

\[ \iint_{D} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y} \mathrm{~d} x \mathrm{~d} y=\oint_{\partial D} P \mathrm{~d} y-Q \mathrm{~d} x \]

第一类曲面积分

设\(\Sigma\)为三维空间中的一个光滑曲面，函数\(f(x,y)\)在\(\Sigma\)上有界。把\(\Sigma\)上任意分为\(n\)个小曲面，第\(k\)个小曲面为\(\Delta S_k\)（该小曲面的面积也同样由\(\Delta S_k\)来表示）。设 (\(\xi_k,\eta_k\)) 是\(\Delta S_k\)上任意取的一点，做乘积\(f(\xi_k,\eta_k)\Delta S_k\)，并作和：

\[ \sum_{k=1}^{n}f(\xi_k,\eta_k)\Delta S_k \]

如果当各小曲面的面积的最大值\(\lambda\to 0\)时，和的极限总是存在，且与曲面\(\Sigma\)的分法及点\((\xi_k,\eta_k)\)的取法无关，就称这此极限为\(f(x,y)\)在曲面\(\Sigma\)上的第一类曲面积分：

\[ \iint_{\Sigma} f(x, y) \mathrm{d} S=\lim _{\lambda \rightarrow 0} \sum_{k=1}^{n} f\left(\xi_{k}, \eta_{k}\right) \Delta S_{k} \]

其中\(\mathrm{d}S\)称为曲面微分。

第二类曲面积分

假设太阳表面为闭球面\(\Sigma\)，将所有的小曲面的通量加起来就得到闭球面\(\Sigma\)的通量，也就是太阳的通量：

\[ \iint_{\Sigma} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} S \]

其中单位法向量\(\boldsymbol{n}\)和面积微分\(\mathrm{d}S\)组成了有向曲面，也称为有向面积微分：

\[ \boldsymbol{n}\mathrm{d}S=\mathrm{d}\boldsymbol{S} \]

所以闭球面\(\Sigma\)的通量又可以写作：

\[ \iint_{\Sigma} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} S=\iint_{\Sigma} \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{S} \]

上述积分是向量场\(\boldsymbol{F}\)在有向面积\(\Sigma\)上的积分，称为第二类曲面积分。

三维的散度和旋度

散度

假设闭曲面\(\Sigma\)围成的体积为\(V\)，和二维的情况一样，通量的密度就是散度：

\[ \operatorname{div} \boldsymbol{F}=\lim _{V \rightarrow 0} \frac{1}{V} \oiint_{\Sigma} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} S \]

假设向量场为\(\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}+R\boldsymbol{k}\)，可以证明散度还有一个偏导形式（较复杂，证明略）：

\[ \operatorname{div}\boldsymbol{F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} \]

旋度

假设三维向量场为\(\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}+R\boldsymbol{k}\)，那么以下向量就为三维空间中的旋度：

\[ \operatorname{curl}\boldsymbol{F}=\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\boldsymbol{i}+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\boldsymbol{j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\boldsymbol{k} \]

该向量的模就是环量密度，方向就是旋转轴向量。

格林公式新形式

通过\(\nabla\)算子，格林公式的通量形式可以改写为：

\[ \oint_{\partial D} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} s=\iint_{D} \nabla \cdot \boldsymbol{F} \mathrm{d} A \]

环量形式可以改写为：

\[ \oint_{\partial D} \boldsymbol{F} \cdot \boldsymbol{\tau} \mathrm{d} s=\iint_{D} \nabla \times \boldsymbol{F} \cdot \boldsymbol{k} \mathrm{d} A \]

环量公式中的\(\boldsymbol{k}\mathrm{d}A\)，其中\(\mathrm{d}A\)指的是\(xy\)面上的平面，\(\boldsymbol{k}\)是\(z\)轴的单位方向向量，也就是\(\mathrm{d}A\)的单位法向量：

因此\(\boldsymbol{k}\mathrm{d}A\)其实表示的是有向平面：

\[ \boldsymbol{k}\mathrm{d}A=\mathrm{d}\boldsymbol{A} \]

进而，格林公式的环量形式还可以改写为第二类曲面积分的形式：

\[ \oint_{\partial D} \boldsymbol{F} \cdot \boldsymbol{\tau} \mathrm{d} s=\iint_{D} \nabla \times \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{A} \]

高斯公式和斯托克斯公式

高斯公式

存在有向光滑闭曲面（或者由几片有向光滑曲面组成）\(\partial\Omega\)，该曲面的正方向\(\boldsymbol{n}\)指向外部。闭曲面\(\partial\Omega\)围成空间闭区域\(\Omega\)，在该闭区域\(\Omega\)上定义有向量函数\(\boldsymbol{F}\)，它的各个分量具有一阶连续偏导数。那么有：

\[ \underbrace{\int_{\boldsymbol{F}} \boldsymbol{F} \cdot \boldsymbol{n d} S}_{\partial \int_{\text {闭曲面的通量 }}}=\underbrace{\iiint_{\Omega} \operatorname{div} \boldsymbol{F} \mathrm{d} V=\iiint_{\Omega} \nabla \cdot \boldsymbol{F} \mathrm{d} V}_{\text {闭曲面围成区域的通量之和 }} \]

该定理称为高斯公式或者散度定理。

斯托克斯公式

假设存在有向光滑闭曲线（或者由几个有向光滑曲线组成）\(\partial\Sigma\)，该有向曲线\(\partial\Sigma\)为有向光滑曲面（或者由几个有向光滑曲面组成）\(\Sigma\)的边界，且有向曲线\(\partial\Sigma\)的方向\(\boldsymbol{\tau}与、Sigma\)的正向\(\boldsymbol{n}\)符合右手法则。在该有向曲面\(\Sigma\)上定义有向量函数\(\boldsymbol{F}\)，它的各个分量具有一阶连续偏导数。那么有：

\[ \underbrace{\oint_{\partial \Sigma} \boldsymbol{F} \cdot \boldsymbol{d} s}_{\text {有向闭曲线的环量 }}=\underbrace{\iint_{\Sigma} \operatorname{curl} \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{S}=\iint_{\Sigma} \nabla \times \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{S}}_{\text {有向闭曲线围成有向曲面的环量之和 }} \]

该定理称为斯托克斯公式。

小结

在二维平面中，格林公式有两种形式，通量形式和环量形式：

\[ \begin{gathered} \oint_{\partial D} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} s=\iint_{D} \operatorname{div} \boldsymbol{F} \mathrm{d} A=\iint_{D} \nabla \cdot \boldsymbol{F} \mathrm{d} A \\ \oint_{\partial D} \boldsymbol{F} \cdot \boldsymbol{\tau} \mathrm{d} s=\iint_{D} \operatorname{curl} \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{A}=\iint_{D} \nabla \times \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{A} \end{gathered} \]

在三维空间中，通量形式扩展为了高斯公式：

\[ \oiint_{\partial \Omega} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} S=\iiint_{\Omega} \operatorname{div} \boldsymbol{F} \mathrm{d} V=\iiint_{\Omega} \nabla \cdot \boldsymbol{F} \mathrm{d} V \]

环量形式扩展为了斯托克斯公式：

\[ \oint_{\partial \Sigma} \boldsymbol{F} \cdot \boldsymbol{\tau} \mathrm{d} s=\iint_{\Sigma} \operatorname{curl} \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{S}=\iint_{\Sigma} \nabla \times \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{S} \]

关于无穷级数这里不列出了，后面在数学物理方法中再列出。

参考文献

《马同学的多变量微积分课程》
感兴趣的可以购买他的课程，写的很好（强烈推荐）！！！