多元函数微分

多元函数及其邻域

二元函数的严格定义：
假设 $D$ 是二维向量 $(x,y)$ 的集合， $D$ 上的二元函数 $\ f$ 是一个映射法则，它对 $D$ 内的每一个有序对 $(x,y)$ 指定唯一的一个实数：

z=f(x,y),\quad (x,y)\in D

如果用 $P$ 来代替 $(x,y)$ 的话，也可以写作：

z=f(P),\quad P\in D

$D$ 称为 $f$ 的定义域， $x、y$ （或 $(x,y)$ ，或 $P$ ）称为 $f$ 的自变量， $z$ 称为 $f$ 的因变量。

如果定义域 $D$ 是更高维的向量的集合，也就是说自变量为更高维的向量，那么
$f$ 可以称为多元函数，也叫作多变量函数。

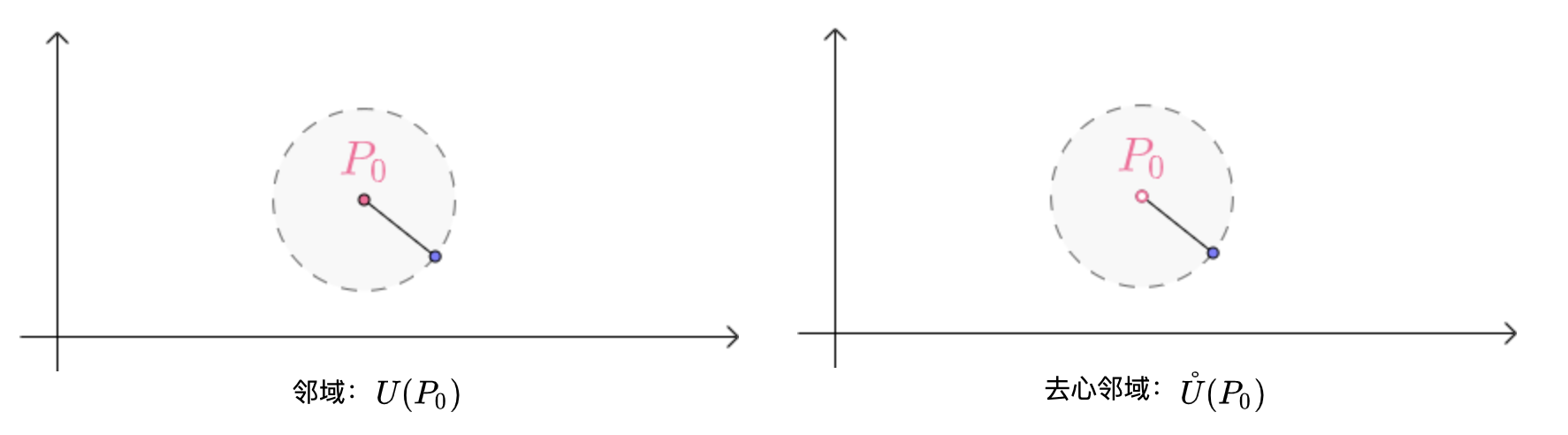
邻域和去心邻域：

二维向量的邻域要比一维向量的复杂。对于二维向量 $P_0(x_0,y_0)$ 而言，半径为 $\delta$ 邻域可以表示为平面点集：

U(P_0,\delta)=\{(x,y)\ |\ (x-x_0)^2 + (y-y_0)^2 < \delta^2\}

多元函数极限和连续

聚点：
如果对于任意给定的 $\delta > 0$ ，点 $P$ 的去心邻域 $\mathring{U}(P,\delta)$ 内总有平面点集 $E$ 中的点，那么称点 $P$ 为 $E$ 的聚点。
定义聚点是为了保证，从 $P_0(x_0,y_0)$ 的某去心邻域内的某一点 $P(x,y)$ 出发，至少能找到一串完全在 E 中的点来靠近 $P_0$
二元函数极限的定义：
设二元函数 $f(x,y)$ 的定义域为 $D，P_0(x_0,y_0)$ 是 $D$ 的聚点。如果存在常数 $L$ ，对于任意给定的正数 $\epsilon$ ，总存在正数 $\delta$ ，使得当点 $P(x,y)$ 满足下列条件时：
$(x,y)\in D\cap \mathring{U}(P_0,\delta)$
都有：
$|f(x,y)-L| < \epsilon$
成立，那么就称常数 $L$ 为函数 $f(x,y)$ 当 $(x,y)\to(x_0,y_0)$ 时的极限，记作：
$\lim_{(x,y)\to(x_0,y_0)}f(x,y)=L\quad 或、quad f(x,y)\to L\ \big(\ (x,y)\to(x_0,y_0)\ \big)$
因为这是二元函数的极限，所以也称作二重极限。
连续：
设二元函数 $f(x,y)$ 的定义域为 $D$ ， $P_0(x_0,y_0)$ 是 $D$ 的聚点，且 $P_0\in D$ ，如果：
$\lim_{(x,y)\to(x_0,y_0)}f(x,y)=f(x_0,y_0)$
那么称函数 $f(x,y)$ 在点 $P_0(x_0,y_0)$ 连续。

全微分

设函数 $z=f(x,y)$ 在点 $(x_0,y_0)$ 的某邻域内有定义，假设：

\Delta x=x-x_0,\quad \Delta y=y-y_0

如果函数 $z=f(x,y)$ 在点 $(x_0,y_0)$ 的全增量：

\Delta z=f(x_0+\Delta x, y_0+\Delta y)-f(x_0, y_0)

可以表示为：

\Delta z=A\Delta x+B\Delta y+o(\rho)=A\Delta x+B\Delta y+\epsilon_1\Delta x+\epsilon_2\Delta y

其中 $A、B$ 不依赖于 $\Delta x、\Delta y$ ，且：

\rho=\sqrt{(\Delta x)^2+(\Delta y)^2},\quad \lim_{\Delta x\to 0}\epsilon_1=0,\quad \lim_{\Delta y\to 0}\epsilon_2=0

那么称 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处可微分，而 $A\Delta x+B\Delta y$ 称为 $z=f(x,y)$ 在点 $(x_0,y_0)$ 处的全微分（或称为切平面），记作 $\mathrm{d}z$ ，即：

\mathrm{d}z=A\mathrm{d}x+B\mathrm{d}y

可以类比单变量微分的定义，单变量微积分是以直线代替曲线，双变量全微分是以平面代替曲线。

偏导数

关于 $x$ 的偏导数：
$\left.\frac{\partial f}{\partial x}\right|_{(x_0,y_0)}=\left.\frac{\mathrm{d}}{\mathrm{d}x}f(x,y_0)\right|_{x=x_0}=\lim_{h\to 0}\frac{f(x_0+h,y_0)-f(x_0,y_0)}{h}$
关于 $y$ 的偏导数：
$\left.\frac{\partial f}{\partial y}\right|_{(x_0,y_0)}=\left.\frac{\mathrm{d}}{\mathrm{d}y}f(x_0,y)\right|_{y=y_0}=\lim_{h\to 0}\frac{f(x_0,y_0+h)-f(x_0,y_0)}{h}$
与全微分的关系：
如果函数 $z=f(x,y)$ 在点 $(x_0,y_0)$ 可微分，那么该函数在点 $(x_0,y_0)$ 的偏导数 $f_x(x_0,y_0)、f_y(x_0,y_0)$ 必定存在，且 $z=f(x,y)$ 在点 $(x_0,y_0)$ 的全微分为：
$\mathrm{d}z=f_x(x_0,y_0)\mathrm{d}x+f_y(x_0,y_0)\mathrm{d}y$

方向导数与梯度

对于二元函数 $z=f(x,y)$ ，沿某单位向量：

\boldsymbol{u}=\begin{pmatrix}u_1\\u_2\end{pmatrix}

在 $(x_0,y_0)$ 点的方向导数为：

\left.\frac{\partial f}{\partial u}\right|_{(x_0,y_0)}=\lim_{t\to 0}\frac{f(x_0+tu_1, y_0+tu_2)-f(x_0,y_0)}{t},\quad t\in\mathbb{R}

单位向量还可以用该向量的方向余弦 $\cos\alpha$ 和 $\cos\beta$ 表示，即：

\boldsymbol{u}=\begin{pmatrix}u_1\\u_2\end{pmatrix}=\begin{pmatrix}\cos\alpha\\\cos\beta\end{pmatrix}

所以方向导数也常表示为：

\left.\frac{\partial f}{\partial u}\right|_{(x_0,y_0)}=\lim_{t\to 0}\frac{f(x_0+t\cos\alpha, y_0+t\cos\beta)-f(x_0,y_0)}{t},\quad t\in\mathbb{R}

模长：该方向向量的模长是方向导数的最大值。
方向：该方向向量的方向正是取得最大方向导数的方向。
投影：它向某单位向量 $\boldsymbol{u}$ 的投影就是对应的方向导数。

该方向向量就称为梯度，记作：

\nabla f(x_0,y_0)=grad f(x_0,y_0)=\begin{pmatrix}f_x(x_0,y_0)\\f_y(x_0,y_0)\end{pmatrix}=f_x(x_0,y_0)\boldsymbol{i}+f_y(x_0,y_0)\boldsymbol{j}

直观的理解就是：

沿着梯度向量方向走，能以最快的速度到达山顶。
逆着梯度向量方向走，能以最快的速度到达山脚。
和梯度向量方向垂直，此时坡度为 0，即不上山也不下山。

全导数

若 $z=f(x,y)$ 是可微分的，而 x 和 y 是 t 的可导函数，则 z 是 t 的可导函数，并且：

\frac{\mathrm{d}z}{\mathrm{d}t}=\frac{\partial z}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}t}+\frac{\partial z}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}t}

这个导数可以看作过切点的曲线的导数，所以又被称为全导数。

总结：

\begin{array}{c|c} \hline \quad \quad&\quad 描述、quad &\quad 公式 \quad\\ \hline \\ \quad 偏导数 \quad&\quad \begin{aligned}y=y_0\ 和、x=x_0\ 两平面、\ \\与曲面相交所得曲线的导数、end{aligned}\quad&\quad f_x=\frac{\partial f}{\partial x},f_y=\frac{\partial f}{\partial y}\quad \\ \\ \hline \\ \quad 方向导数 \quad&\quad\begin{aligned}垂直于 xy 的平面、quad\quad\ \ \\与曲面相交所得曲线的导数、\ \end{aligned}\quad&\quad \frac{\partial f}{\partial u}=f_x\cos\alpha+f_y\cos\beta\quad\\ \\ \hline \\ \quad 全导数 \quad&\quad\begin{aligned}垂直于 xy 的曲面、quad\quad\ \ \\与曲面相交所得曲线的导数、\ \end{aligned}\quad&\quad\frac{\mathrm{d}z}{\mathrm{d}t}=\frac{\partial z}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}t}+\frac{\partial z}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}t}\quad\\ \\ \hline \end{array}

雅可比矩阵

二元函数的导数：
二元函数 $z=f(x,y)$ 的微分，微分在 $\mathrm{d}x\mathrm{d}y\mathrm {d}z$ 坐标系中的方程为：
$\mathrm{d}z=f_x\mathrm{d}x+f_y\mathrm{d}y$
可以改写为矩阵的形式：
$\underbrace{\begin{pmatrix}\mathrm{d}z\end{pmatrix}}_ {\boldsymbol{d_z}}\quad=\quad\underbrace{\begin{pmatrix} f_x&f_y\end{pmatrix}}_{T}\quad\underbrace{\begin{pmatrix} \mathrm{d}x\\\mathrm{d}y\end{pmatrix}}_{\boldsymbol{d_{xy} }}$
或者写作：
$\boldsymbol{d_z}=T\boldsymbol{d_{xy}}$
一般的多元函数：
$y=f(x_1,x_2,\cdots,x_n),\quad (y,x_1,x_2,\cdots, x_n\in\mathbb{R})$
如果可微的话，那么微分方程为：
$\mathrm{d}y=f_{x_1}\mathrm{d}x_1+f_{x_2}\mathrm{d}x_2 +\cdots+f_{x_n}\mathrm{d}x_n$
可以改写为矩阵的形式：
$\underbrace{\begin{pmatrix}\mathrm{d}y\end{pmatrix}}_ {\boldsymbol{d_y}}\quad=\quad\underbrace{\begin{pmatrix}f_ {x_1}&f_{x_2}&\cdots&f_{x_n}\end{pmatrix}}_{T} \quad\underbrace{\begin{pmatrix}\mathrm{d}x_1\\\mathrm{d} x_2\\\vdots\\\mathrm{d}x_b\end{pmatrix}}_{\boldsymbol{d_ {x}}}$
或者写作：
$\boldsymbol{d_y}=T\boldsymbol{d_{x}}$
其中矩阵 T 就是该多元函数的导数。
二元方程组的导数：
$\begin{cases} \mathrm{d}z=\frac{\partial f}{\partial x}\mathrm{d}x +\frac{\partial f}{\partial y}\mathrm{d}y\\ \\ \mathrm{d}w=\frac{\partial g}{\partial x}\mathrm{d}x +\frac{\partial g}{\partial y}\mathrm{d}y \end{cases}$
可以写成矩阵的形式：
$\underbrace{\begin{pmatrix}\mathrm{d}z\\\mathrm{d}w\end{pmatrix}}_{\boldsymbol{d_{v}}}\quad=\quad\underbrace{\begin{pmatrix}\frac{\partial f}{\partial x}&\frac{\partial f}{\partial y}\\\frac{\partial g}{\partial x}&\frac{\partial g}{\partial y}\end{pmatrix}}_{T}\quad\underbrace{\begin{pmatrix}\mathrm{d}x\\\mathrm{d}y\end{pmatrix}}_{\boldsymbol{d_{u}}}$
或者写作：
$\boldsymbol{d_{v}}=T\boldsymbol{d_{u}}$
其中矩阵 T 就是该方程组所代表的函数的导数。
雅可比矩阵（多元方程组的导数矩阵）：
假如 $f_1,f_2,\cdots,f_n$ 都是 $x_1,x_2,\cdots,x_m$ 的函数，并且相对于各个自变量的偏微分都存在，那么定义 T 为：
$T=\frac{\partial (f_1,f_2,\cdots,f_n)}{\partial (x_1,x_2,\cdots,x_m)}=\begin{pmatrix}\frac{\partial f_1}{\partial x_1}&\frac{\partial f_1}{\partial x_2}&\cdots&\frac{\partial f_1}{\partial x_m}\\\frac{\partial f_2}{\partial x_1}&\frac{\partial f_2}{\partial x_2}&\cdots&\frac{\partial f_2}{\partial x_m}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial f_n}{\partial x_1}&\frac{\partial f_n}{\partial x_2}&\cdots&\frac{\partial f_n}{\partial x_m}\end{pmatrix}$
该矩阵 $T$ 称为雅可比矩阵。因为雅可比矩阵的英文名为 Jacobian Matrix，所以上述矩阵又常写作：
$J=\frac{\partial (f_1,f_2,\cdots,f_n)}{\partial (x_1,x_2,\cdots,x_m)}$
海森矩阵：
一元导数 $y=f(x)$ 的二阶导数就是连续两次使用 $\frac{\mathrm{d}}{\mathrm{d}x}$ ：
$\frac{\mathrm{d}^2y}{\mathrm{d}x^2}=\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)$
类似的，二元函数 $z=f(x,y)$ 的二阶导数就是连续两次计算雅可比矩阵：
$\frac{\partial^2 z}{\partial(x,y)^2}=\frac{\partial }{\partial(x,y)}\left(\frac{\partial z}{\partial(x,y)}\right)=\begin{pmatrix}f_{xx}&f_{xy}\\f_{yx}&f_{yy}\end{pmatrix}$
二阶导数又称为海森矩阵（Hessian Matrix），所以常用 H 来表示这个矩阵：
$H=\frac{\partial^2 z}{\partial(x,y)^2}=\begin{pmatrix}f_{xx}&f_{xy}\\f_{yx}&f_{yy}\end{pmatrix}$
海森矩阵可以判断图像的凹凸性。

此外关于隐函数的求导，多元函数的极值求法这里不再列出，详细可以参考相关书籍。

重积分

二重积分

设 $f(x,y)$ 是有界闭区域 $D$ 上的有界函数，将闭区域 $D$ 任意分成 $n$ 个小闭区域：

\Delta A_1,\Delta A_2,\cdots,\Delta A_i,\cdots,\Delta A_n

其中 $\Delta A_i$ 表示第 $i$ 个小闭区域，也表示它的面积，规定 $\Delta A_i$ 中最长的直径（一个闭区域的直径是指区域上任意两点间距离的最大者）为 $\lambda$ ，在每个 $\Delta A_i$ 内任取一点 $(x_i,y_i)$ ，可以得到级数：

\sum_{i=0}^{n}f(x_i,y_i)\Delta A_i

如果当 $\lambda\to 0$ 时，无论如何划分闭区域 $D$ ，无论怎样选取 $(x_i,y_i)$ ，该级数的极限总是存在，那么称此极限为函数 $f(x,y)$ 在闭区域 $D$ 上的二重积分，记作：

\iint_{D} f(x, y) \mathrm{d} A=\lim _{\lambda \rightarrow 0} \sum_{i=0}^{n} f\left(x_{i}, y_{i}\right) \Delta A_{i}

其中 $f(x,y)$ 称为被积函数， $\mathrm{d}A$ 称为面积微分， $x$ 与 $y$ 称为积分变量， $D$ 称为积分区域。

二重积分的性质

设 $f(x,y)，g(x,y)$ 都是有界闭区域 $D$ 上的有界函数， $\alpha、\beta$ 为常数，则：

齐次性：
$\iint_{D} \alpha f(x, y) \mathrm{d} A=\alpha \iint_{D} f(x, y) \mathrm{d} A$
可加性：
$\iint_{D}(f(x, y)+g(x, y)) \mathrm{d} A=\iint_{D} f(x, y) \mathrm{d} A+\iint_{D} g(x, y) \mathrm{d} A$
推论：
$\iint_{D}(\alpha f(x, y) \pm \beta g(x, y)) \mathrm{d} A=\alpha \iint_{D} f(x, y) \mathrm{d} A \pm \beta \iint_{D} g(x, y) \mathrm{d} A$
区域可加性：
如果闭区域 $D$ 被有限条曲线分为有限个部分闭区域，那么 $D$ 上的二重积分等于各部分闭区域上的二重积分之和。
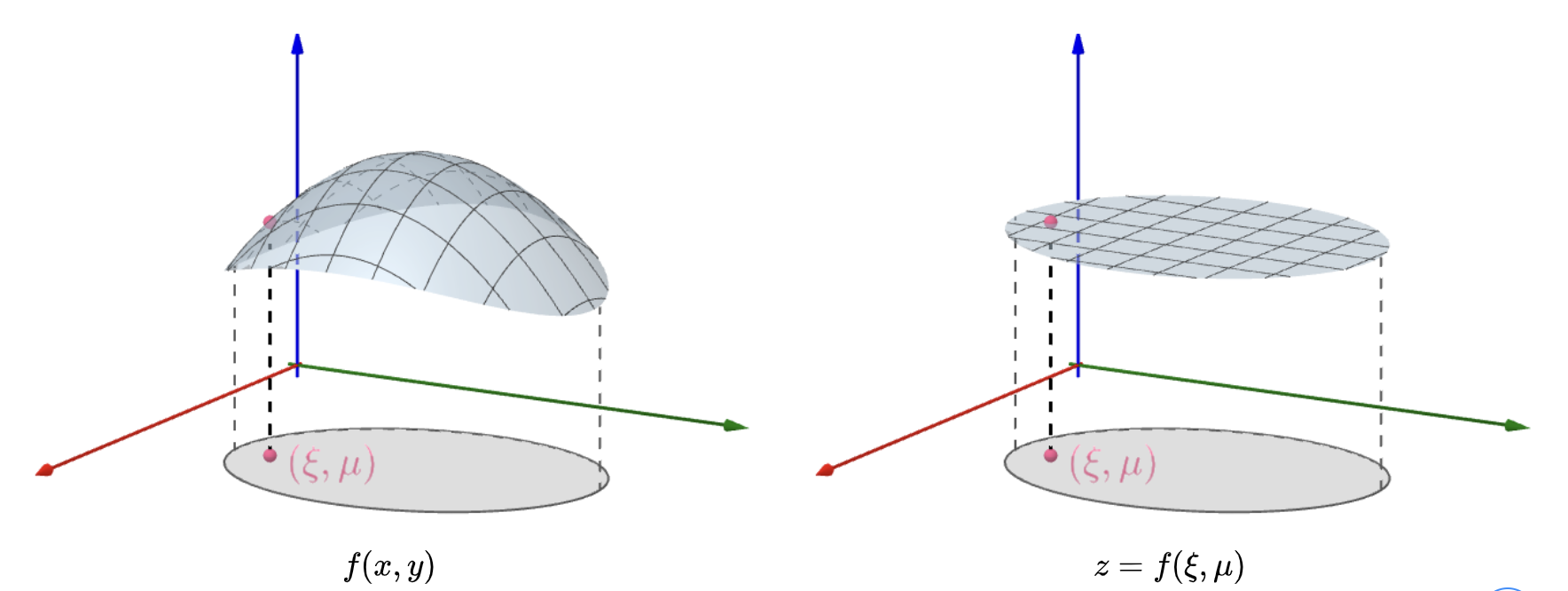
二重积分中值定理：
设函数 $f(x,y)$ 在闭区域 $D$ 上连续， $A$ 是区域 $D$ 的面积，则在 $D$ 上至少存在一点 $(\xi,\mu)$ ，使得：
$\iint_{D} f(x, y) \mathrm{d} A=f(\xi, \mu) A$

二重积分法

弱富比尼定理

设有矩形区域 $R$ ：

R=\{(x,y)|a\le x\le b,c\le y\le d\}

若 $f(x,y)$ 在区域 $R$ 上连续，则：

\iint_{R} f(x, y) \mathrm{d} A=\int_{c}^{d}\left[\int_{a}^{b} f(x, y) \mathrm{d} x\right] \mathrm{d} y=\int_{a}^{b}\left[\int_{c}^{d} f(x, y) \mathrm{d} y\right] \mathrm{d} x

将二重积分变为，先积 x 后积 y（或先积 y 后积 x）的二次积分。

强富比尼定理

若 $f(x,y)$ 在区域 $D$ 上连续：

若区域 D 为 $a \le x \le b, g_1(x) \le y \le g_2(x)$ ，其中 $g_1、g_2$ 在 $[a,b]$ 上连续，则：

\iint_{D} f(x, y) \mathrm{d} A=\int_{a}^{b}\left[\int_{g_{1}(x)}^{g_{2}(x)} f(x, y) \mathrm{d} y\right] \mathrm{d} x

若区域 D 为 $c \le y \le d, h_1(y) \le x \le h_2(y)$ ，其中 $h_1、h_2$ 在 $[c,d]$ 上连续，则：

\iint_{D} f(x, y) \mathrm{d} A=\int_{c}^{d}\left[\int_{h_{1}(y)}^{h_{2}(y)} f(x, y) \mathrm{d} x\right] \mathrm{d} y

可见，和富比尼定理的较弱形式不一样，这里是不能交换积分顺序的。

坐标系变换

有时候切换一下坐标系问题会变得简单的多，为此研究在坐标变换后的多重积分也是很有价值的。

在区域 D 上，如果 $xy$ 直角坐标系和 $uv$ 直角坐标系之间存在如下的坐标变换函数，且 $x(u,v)、y(u,v)$ 在区域 D 上有一阶连续偏导数（这是为了保证可以找到最佳线性近似）：

\begin{cases} x=x(u,v)\\ y=y(u,v) \end{cases}

如果雅可比行列式存在且不为 0：

|J|=|\frac{\partial(x,y)}{\partial(u,v)}|=\begin{vmatrix}\frac{\partial x}{\partial u }&\frac{\partial x}{\partial v}\\\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}\end{vmatrix}\ne 0

则区域 D 上在 $xy$ 直角坐标系下的面积为：

\iint_{D} \mathrm{~d} x \mathrm{~d} y=\iint_{D}\|J\| \mathrm{d} u \mathrm{~d} v

所以， $z=f(x,y)$ 在区域 D 上的体积为（在 $xyz$ 直角坐标系下的体积）：

\iint_{D} f(x, y) \mathrm{d} x \mathrm{~d} y=\iint_{D} f(x(u, v), y(u, v))\|J\| \mathrm{d} u \mathrm{~d} v

三重积分

设 $f(x,y,z)$ 是有界闭区域 $\Omega$ 上的有界函数，将闭区域 $\Omega$ 任意分成 $n$ 个小闭区域：

\Delta V_1,\Delta V_2,\cdots,\Delta V_i,\cdots,\Delta V_n

其中 $\Delta V_i$ 表示第 $i$ 个小闭区域，也表示它的体积，规定 $\Delta V_i$ 中最大的体积为 $\lambda$ ：

\lambda=\max(\Delta V_i)

在每个 $\Delta V_i$ 内任取一点 $(\xi_i,\mu_i,\zeta_i)$ ，可以得到级数：

\sum_{i=0}^{n}f(\xi_i,\mu_i,\zeta_i)\Delta V_i

如果当 $\lambda\to 0$ 时，无论如何划分闭区域 $\Omega$ ，无论怎样选取 $(\xi_i,\mu_i,\zeta_i)$ ，该级数的极限总是存在，那么称此极限为函数 $f(x,y,z)$ 在闭区域 $\Omega$ 上的三重积分，记作：

\iiint_{\Omega} f(x, y, z) \mathrm{d} V=\lim _{\lambda \rightarrow 0} \sum_{i=0}^{n} f\left(\xi_{i}, \mu_{i}, \zeta_{i}\right) \Delta V_{i}

其中 $f(x,y,z)$ 称为被积函数， $\mathrm{d}V$ 称为体积微分， $x、y$ 以及 $z$ 称为积分变量， $\Omega$ 称为积分区域。

三重积分法

富比尼定理

区域 E 可以表示为：

E=\{(x,y,z)|a\le x\le b,g_1(x)\le y\le g_2(x), u_1(x,y)\le z\le u_2(x,y)\}

那么通过富比尼定理，函数 $f(x,y,z)$ 在区域 E 上的三重积分可以如下计算：

\begin{aligned} \iiint_{E} f(x, y, z) \mathrm{d} V &=\iint_{D}\left[\int_{u_{1}(x, y)}^{u_{2}(x, y)} f(x, y, z) \mathrm{d} z\right] \mathrm{d} A \\ &=\int_{a}^{b} \int_{g_{1}(x)}^{g_{2}(x)} \int_{u_{1}(x, y)}^{u_{2}(x, y)} f(x, y, z) \mathrm{d} z \mathrm{~d} y \mathrm{~d} x \end{aligned}

这样就将三重积分划为了方便计算的三次积分。

坐标系变换

同样变换坐标系是为了简化问题。这里直接给出坐标系变换积分公式：

柱面坐标系的体积微分：
通过雅可比行列式 $|J|$ ，可得柱面坐标系函数 $w=f(\rho,\theta,z)$ 在区域 $\Omega$ 上的三重积分为：
$\begin{aligned} \iiint_{\Omega} f(\rho, \theta, z) \mathrm{d} V &=\iiint_ {\Omega} f(\rho, \theta, z)\|J\| \mathrm{d} \rho \mathrm{d} \theta \mathrm{d} z \\ &=\iiint_{\Omega} f(\rho, \theta, z) \rho \mathrm{d} \rho \mathrm{d} \theta \mathrm{d} z \end{aligned}$
其中 $\rho\mathrm{d}\rho\mathrm{d}\theta\mathrm{d}z$ 称为柱面坐标系的体积微分。
球面坐标系的体积微分：
通过雅可比行列式 $|J|$ ，可得球面坐标系函数 $w=f(r,\varphi,\theta)$ 在区域 $\Omega$ 上的三重积分为：
$\begin{aligned} \iiint_{\Omega} f(r, \varphi, \theta) \mathrm{d} V &=\iiint_ {\Omega} f(r, \varphi, \theta)\|J\| \mathrm{d} r \mathrm{~d} \varphi \mathrm{d} \theta \\ &=\iint_{\Omega} \iint(r, \varphi, \theta) r^{2} \sin \varphi \mathrm{d} r \mathrm{~d} \varphi \mathrm{d} \theta \end{aligned}$
其中 $r^2\sin\varphi\mathrm{d}r\mathrm{d}\varphi\mathrm{d}\theta$ 称为球面坐标系的体积微分。

曲线积分与曲面积分

第一类曲线积分

设 $L$ 为 $xOy$ 面内的一条光滑曲线弧，函数 $f(x,y)$ 在 $L$ 上有界。在 $L$ 上任意插入一点列 $P_0、P_1，\cdots、P_{n}$ ，把 $L$ 分成 $n$ 个小段。设第 $k$ 个小段的长度为 $\Delta s_k$ 。又 $(\xi_k,\eta_k)$ 为第 $k$ 个小段上任意取定的一点，做乘积 $f(\xi_k,\eta_k)\Delta s_k$ ，并作和：

\sum_{k=1}^{n}f(\xi_k,\eta_k)\Delta s_k

如果当各小弧段的长度的最大值 $\lambda\to 0$ 时，这和的极限总是存在，且与曲线 $L$ 的分法及点 $(\xi_k,\eta_k)$ 的取法无关，那么称此极限为函数 $f(x,y)$ 在曲线 $L$ 上的第一类曲线积分，记作：

\int_L f(x,y)\mathrm{d}s=\lim_{\lambda\to 0}\sum_{k=1}^{n}f(\xi_k,\eta_k)\Delta s_k

其中 $\mathrm{d}s$ 称为弧微分。

物理意义：
第一类曲线积分的物理意义还是很明显的，之前介绍过，如果 $\mu(x,y)$ 是曲线 $L$ 的密度函数时，如下计算的是曲线质量：
$m=\int_L \mu(x,y)\mathrm{d}s$
而如果 $\delta(x,y)$ 是曲线 $L$ 的电荷密度函数，那么如下计算的就是曲线的电荷量：
$c=\int_L \delta(x,y)\mathrm{d}s$
几何意义：
第一类曲线积分 $\int_L f(x,y)\mathrm{d}s$ 的几何意义就是求曲线 L 与曲面 $z=f(x,y)$ 之间的面积：
性质：
- 性质 1：设 $\alpha、\beta$ 为常数，则：
$\int_L[\alpha f(x,y)+\beta g(x,y)]\mathrm{d}s=\alpha\int_L f(x,y)\mathrm{d}s+\beta\int_L g(x,y)\mathrm{d}s$
- 性质 2：设光滑曲线 $L$ 可分为两个光滑曲线 $L_1$ 和 $L_2$ ，则：
$\int_L f(x,y)\mathrm{d}s=\int_{L_1} f(x,y)\mathrm{d}s+\int_{L_2} f(x,y)\mathrm{d}s$
- 性质 3：设在光滑曲线 L 上有 $f(x,y)\le g(x,y)$ ，则：
$\int_L f(x,y)\mathrm{d}s\le\int_{L} g(x,y)\mathrm{d}s$

第二类曲线积分

设 $L$ 为 $xOy$ 面内从 $A$ 点到 $B$ 点的一条光滑曲线弧，函数 $P(x,y)、Q(x,y)$ 在 $L$ 上有界。在 $L$ 上任意插入一点列 $P_0、P_1，\cdots、P_{n}$ ，把 $L$ 分成 $n$ 个有向小弧段：

\overbrace{P_{k-1} P_{k}}, \quad\left(k=1,2, \cdots, n, P_{0}=A, P_{n}=B\right)

设 $\Delta x_k=x_k-x_{k-1}，\Delta y_k=y_k-y_{k-1}$ ，点 $(\xi_k,\eta_k)$ 为 $\overbrace{P_{k-1} P_{k}}$ 上任意取定的点，做乘积 $P(\xi_k,\eta_k)\Delta x_i$ ，并作和：

\sum_{k=1}^{n}P(\xi_k,\eta_k)\Delta x_k,\quad \sum_{k=1}^{n}Q(\xi_k,\eta_k)\Delta y_k

如果当各小弧段的长度的最大值 $\lambda\to 0$ 时，和的极限总是存在，且与曲线 $L$ 的分法及点 $(\xi_k,\eta_k)$ 的取法无关，就称这两个极限为 $P(x,y)$ 在有向曲线 $\ L$ 上对坐标 $\ x$ 的曲线积分：

\int_L P(x,y)\mathrm{d}x=\lim_{\lambda\to 0}\sum_{k=1}^{n}P(\xi_k,\eta_k)\Delta x_k

以及 $Q(x,y)$ 在有向曲线 $\ L$ 上对坐标 $\ y$ 的曲线积分：

\int_L Q(x,y)\mathrm{d}y=\lim_{\lambda\to 0}\sum_{k=1}^{n}Q(\xi_k,\eta_k)\Delta y_k

以上两个积分也称为第二类曲线积分。

性质：
- 性质 1：设 $\alpha、\beta$ 为常数，则：
$\int_L[\alpha\boldsymbol{F_1}(x,y)+\beta\boldsymbol{F_2}(x,y)]\cdot\mathrm{d}\boldsymbol{s}=\alpha\int_L\boldsymbol{F_1}(x,y)\cdot\mathrm{d}\boldsymbol{s}+\beta\int_L\boldsymbol{F_2}(x,y)\cdot\mathrm{d}\boldsymbol{s}$
- 性质 2：设有向光滑曲线 $L$ 可分为两个光滑有向曲线 $L_1$ 和 $L_2$ ，则：
$\int_L \boldsymbol{F}(x,y)\cdot\mathrm{d}\boldsymbol{s}=\int_{L_1} \boldsymbol{F}(x,y)\cdot\mathrm{d}\boldsymbol{s}+\int_{L_2}\boldsymbol{F}(x,y)\cdot\mathrm{d}\boldsymbol{s}$
- 性质 3：设 $L$ 是有向光滑曲线， $L^-$ 是 $L$ 的反向曲线，则：
$\int_L \boldsymbol{F}(x,y)\cdot\mathrm{d}\boldsymbol{s}=-\int_{L^-} \boldsymbol{F}(x,y)\cdot\mathrm{d}\boldsymbol{s}$

两类曲线积分的关系

区别

第一类曲线积分针对的是曲线，而第二类曲线积分针对的是有向曲线。
第一类曲线积分，作用在曲线上的是标量；而第二类曲线积分，作用在曲线上的是向量。

联系

因为弧微分和有向弧微分的关系为 $\boldsymbol{\tau}\mathrm{d}s=\mathrm{d}\boldsymbol{s}$ ，所以：

\int_L \boldsymbol{F}\cdot\boldsymbol{\tau}\mathrm{d}s=\int_L \boldsymbol{F}\cdot\mathrm{d}\boldsymbol{s}

左边为第一类曲线积分，右边为第二类曲线积分，可见这两类积分是可以互相转化的。

二维的散度和旋度

通量

在连续向量场 $\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}$ 中的光滑闭曲线 $L$ ， $\boldsymbol{n}$ 为光滑闭曲线 $L$ 的单位法向量（指向闭曲线外部），则 $\boldsymbol{F}$ 穿过 $L$ 的流量，即通量为：

\oint_{L} \boldsymbol{F}\cdot\boldsymbol{n}\mathrm{d}s=\oint_{L}P\mathrm{d}y-Q\mathrm{d}x

需要注意的是，上式从第一类曲线积分变为了第二类曲线积分，曲线的方向为逆时针。

散度

已知水流量为向量场 $\boldsymbol{F}$ 。用曲线 $L_A$ 来表示 A 圆，那么 A 圆的通量为：

T_A=\oint_{L_A} \boldsymbol{F}\cdot\boldsymbol{n}\mathrm{d}s

假设 A 圆对应的面积为 $\Omega_A$ ，圆缩到最小即 $\Omega_A\to 0$ ，同时再除上面积 $\Omega_A$ ，就得到了 $A$ 点在向量场 $\boldsymbol{F}$ 中的通量密度，也称为 A 点在向量场 $\boldsymbol{F}$ 中的散度，即：

\operatorname{div}\boldsymbol{F}(A)=\lim_{\Omega_A\to 0}\frac{1}{\Omega_A}\oint_{L_A} \boldsymbol{F}\cdot\boldsymbol{n}\mathrm{d}s

同样的，也可以算出 C 点的散度 $\operatorname{div}\boldsymbol{F}(C)$ ，两者谁大，就说明哪个水龙头的出水量更大。

环量

在连续向量场 $\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}$ 中的光滑闭曲线 $L$ ， $\boldsymbol{\tau}$ 为光滑闭曲线 $L$ 的单位切向量 $\boldsymbol{\tau}$ （指向逆时针方向），则 $\boldsymbol{F}$ 对于 $L$ 的环量为：

\oint_{L} \boldsymbol{F}\cdot\boldsymbol{\tau}\mathrm{d}s=\oint_{L}P\mathrm{d}x+Q\mathrm{d}y

需要注意的是，上式从第一类曲线积分变为了第二类曲线积分，曲线的方向为逆时针。

旋度

已知水流量为向量场 $\boldsymbol{F}$ 。用曲线 $L_A$ 来表示 $A$ 圆，那么 $A$ 圆的环量为：

H_A=\oint_{L_A} \boldsymbol{F}\cdot\boldsymbol{\tau}\mathrm{d}s

可见，环量会受到圆的大小的影响，所以来排除掉这个影响。假设 A 圆对应的面积为 $\Omega_A$ ，圆缩到最小即 $\Omega_A\to 0$ ，同时再除上面积 $\Omega_A$ ，就得到了 $A$ 点在向量场 $\boldsymbol{F}$ 中的环量密度，也称为 $A$ 点在向量场 $\boldsymbol{F}$ 中的旋度，即：

\operatorname{curl}\boldsymbol{F}(A)=\lim_{\Omega_A\to 0}\frac{1}{\Omega_A}\oint_{L_A} \boldsymbol{F}\cdot\boldsymbol{\tau}\mathrm{d}s

格林公式

格林公式的通量形式：

某光滑闭曲线 L 围成闭区域 D，定义在闭区域 D 上的向量场 $\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}$ ，它的分量具有一阶连续偏导数，则 $\boldsymbol{F}$ 关于 L 的通量，可通过闭区域 D 上的散度求出：

\underbrace{\oint_{L} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} s=\oint_{L} P \mathrm{~d} y-Q \mathrm{~d} x}_{\text {闭曲线的通量 }}=\underbrace{\iint_{D} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y} \mathrm{~d} x \mathrm{~d} y}_{\text {闭曲线围成区域的通量之和 }}

格林公式的环量形式：

某光滑闭曲线 L 围成闭区域 D，定义在闭区域 D 上的向量场 $\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}$ ，它的分量具有一阶连续偏导数，则 $\boldsymbol{F}$ 关于 L 的环量，可通过闭区域 D 上的旋度求出：

\underbrace{\oint_{L} \boldsymbol{F} \cdot \boldsymbol{\tau} \mathrm{d} s=\oint_{L} P \mathrm{~d} x+Q \mathrm{~d} y}_{\text {闭曲线的环量 }}=\underbrace{\iint_{D} \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \mathrm{~d} x \mathrm{~d} y}_{\text {闭曲线围成区域的环量之和 }}

二重积分的基本定理

\iint_{D} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y} \mathrm{~d} x \mathrm{~d} y=\oint_{\partial D} P \mathrm{~d} y-Q \mathrm{~d} x

第一类曲面积分

设 $\Sigma$ 为三维空间中的一个光滑曲面，函数 $f(x,y)$ 在 $\Sigma$ 上有界。把 $\Sigma$ 上任意分为 $n$ 个小曲面，第 $k$ 个小曲面为 $\Delta S_k$ （该小曲面的面积也同样由 $\Delta S_k$ 来表示）。设 ( $\xi_k,\eta_k$ ) 是 $\Delta S_k$ 上任意取的一点，做乘积 $f(\xi_k,\eta_k)\Delta S_k$ ，并作和：

\sum_{k=1}^{n}f(\xi_k,\eta_k)\Delta S_k

如果当各小曲面的面积的最大值 $\lambda\to 0$ 时，和的极限总是存在，且与曲面 $\Sigma$ 的分法及点 $(\xi_k,\eta_k)$ 的取法无关，就称这此极限为 $f(x,y)$ 在曲面 $\Sigma$ 上的第一类曲面积分：

\iint_{\Sigma} f(x, y) \mathrm{d} S=\lim _{\lambda \rightarrow 0} \sum_{k=1}^{n} f\left(\xi_{k}, \eta_{k}\right) \Delta S_{k}

其中 $\mathrm{d}S$ 称为曲面微分。

第二类曲面积分

假设太阳表面为闭球面 $\Sigma$ ，将所有的小曲面的通量加起来就得到闭球面 $\Sigma$ 的通量，也就是太阳的通量：

\iint_{\Sigma} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} S

其中单位法向量 $\boldsymbol{n}$ 和面积微分 $\mathrm{d}S$ 组成了有向曲面，也称为有向面积微分：

\boldsymbol{n}\mathrm{d}S=\mathrm{d}\boldsymbol{S}

所以闭球面 $\Sigma$ 的通量又可以写作：

\iint_{\Sigma} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} S=\iint_{\Sigma} \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{S}

上述积分是向量场 $\boldsymbol{F}$ 在有向面积 $\Sigma$ 上的积分，称为第二类曲面积分。

三维的散度和旋度

散度

假设闭曲面 $\Sigma$ 围成的体积为 $V$ ，和二维的情况一样，通量的密度就是散度：

\operatorname{div} \boldsymbol{F}=\lim _{V \rightarrow 0} \frac{1}{V} \oiint_{\Sigma} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} S

假设向量场为 $\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}+R\boldsymbol{k}$ ，可以证明散度还有一个偏导形式（较复杂，证明略）：

\operatorname{div}\boldsymbol{F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}

旋度

假设三维向量场为 $\boldsymbol{F}=P\boldsymbol{i}+Q\boldsymbol{j}+R\boldsymbol{k}$ ，那么以下向量就为三维空间中的旋度：

\operatorname{curl}\boldsymbol{F}=\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\boldsymbol{i}+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\boldsymbol{j}+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\boldsymbol{k}

该向量的模就是环量密度，方向就是旋转轴向量。

格林公式新形式

通过 $\nabla$ 算子，格林公式的通量形式可以改写为：

\oint_{\partial D} \boldsymbol{F} \cdot \boldsymbol{n} \mathrm{d} s=\iint_{D} \nabla \cdot \boldsymbol{F} \mathrm{d} A

环量形式可以改写为：

\oint_{\partial D} \boldsymbol{F} \cdot \boldsymbol{\tau} \mathrm{d} s=\iint_{D} \nabla \times \boldsymbol{F} \cdot \boldsymbol{k} \mathrm{d} A

环量公式中的 $\boldsymbol{k}\mathrm{d}A$ ，其中 $\mathrm{d}A$ 指的是 $xy$ 面上的平面， $\boldsymbol{k}$ 是 $z$ 轴的单位方向向量，也就是 $\mathrm{d}A$ 的单位法向量：

因此 $\boldsymbol{k}\mathrm{d}A$ 其实表示的是有向平面：

\boldsymbol{k}\mathrm{d}A=\mathrm{d}\boldsymbol{A}

进而，格林公式的环量形式还可以改写为第二类曲面积分的形式：

\oint_{\partial D} \boldsymbol{F} \cdot \boldsymbol{\tau} \mathrm{d} s=\iint_{D} \nabla \times \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{A}

高斯公式和斯托克斯公式

高斯公式

存在有向光滑闭曲面（或者由几片有向光滑曲面组成） $\partial\Omega$ ，该曲面的正方向 $\boldsymbol{n}$ 指向外部。闭曲面 $\partial\Omega$ 围成空间闭区域 $\Omega$ ，在该闭区域 $\Omega$ 上定义有向量函数 $\boldsymbol{F}$ ，它的各个分量具有一阶连续偏导数。那么有：

\underbrace{\int_{\boldsymbol{F}} \boldsymbol{F} \cdot \boldsymbol{n d} S}_{\partial \int_{\text {闭曲面的通量 }}}=\underbrace{\iiint_{\Omega} \operatorname{div} \boldsymbol{F} \mathrm{d} V=\iiint_{\Omega} \nabla \cdot \boldsymbol{F} \mathrm{d} V}_{\text {闭曲面围成区域的通量之和 }}

该定理称为高斯公式或者散度定理。

斯托克斯公式

假设存在有向光滑闭曲线（或者由几个有向光滑曲线组成） $\partial\Sigma$ ，该有向曲线 $\partial\Sigma$ 为有向光滑曲面（或者由几个有向光滑曲面组成） $\Sigma$ 的边界，且有向曲线 $\partial\Sigma$ 的方向 $\boldsymbol{\tau}与、Sigma$ 的正向 $\boldsymbol{n}$ 符合右手法则。在该有向曲面 $\Sigma$ 上定义有向量函数 $\boldsymbol{F}$ ，它的各个分量具有一阶连续偏导数。那么有：